asu1

1

-----

140 s

>> n3= [120, 0]; m3=1; q3=tf (n3, m3)

Transfer function: 120 s

>> W1=q1+q2+q3

Transfer function: 16800 s^2 + 56 s + 1

--------------------

140 s

Формируем передаточную функцию Wоу=W2:

>> n4= [0.5]; m4= [420, 1]; W2=tf (n4, m4)

Transfer function: 0.5

---------

420 s + 1

>> WR = W1*W2

Transfer function: 8400 s^2 + 28 s + 0.5

---------------------

58800 s^2 + 140 s

Обратите внимание на то, что в ответе имени функции W(s) нет. Ее имя совпадает с именем произведения W1*W2.

Определение нулей и полюсов передаточной функции W(S).

Нули и полюса определяются с помощью функций: pole(W) и zero(W). Нулями передаточной функции являются корни числителя , а полюсами –

корни знаменателя. Программа имеет вид: >> p=pole(W)

50

p = 0

-0.0024

>> z=zero(W) z =

-0.0017 + 0.0075i -0.0017 - 0.0075i

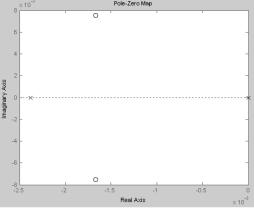
Расположение нулей и полюсов на комплексной плоскости.

Функция pzmap показывает расположение нулей и полюсов передаточной функции на комплексной плоскости S.

>>pzmap(W)

На рисунке (рис. 8.2.) показано расположение нулей (кружки) и полюсов (крестики) на плоскости S. Условием устойчивости разомкнутой системы автоматического управления будет расположение всех корней характеристического уравнения в плоскости корней слева от мнимой оси. Исследуемая система неустойчива, так как один из полюсов равен нулю.

Рис. 8.2 Расположение нулей и полюсов

Исследование качества переходного процесса.

Определим реакцию системы автоматического управления на единичную функцию с помощью функции steр ( ). На этом этапе получаем только график реакции системы.

>> step (W)

Переходный процесс разомкнутой системы автоматического регулирования – расходящийся. Следовательно, система неустойчива. (рис. 8.3.).

51

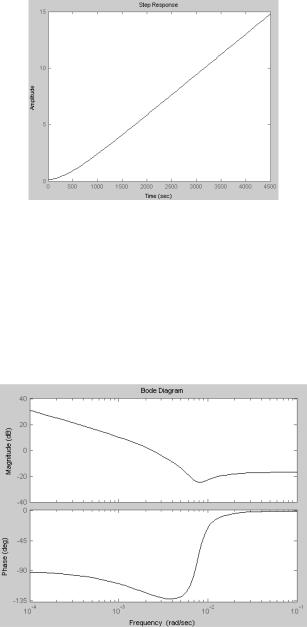
Рис. 8.3. Качество переходного процесса

Частотная характеристика.

Амплитудно – частотная и фазочастотная характеристики строятся с помощью функции bode ( ), полученные функции называются функциями Боде, (рис. 8.4.).

>> bode(W)

Рис. 8.4. Частотная характеристика

Амплитудно-фазовая характеристика.

Амплитудно-фазовую характеристику называют диаграммой Найквиста. Она применяется для анализа устойчивости по критерию Найквиста (рис. 8.5.). >> nyquist(W)

Если амплитудно-фазовая характеристика не охватывает точку с координатами (-1; j0), то система является устойчивой. На рисунке амплитуднофазовая характеристика не охватывает эту точку.

52

Рис. 8.5. Амплитудно – фазовая характеристика

Диаграмма Никольса.

Сетка кривых линий на логарифмической амплитудно-фазовой диаграмме называется диаграммой Никольса. Линиями постоянных значений амплитуды М (показатель колебательности) соответствует децибелы, а линиям постоянных значений N = tg ϕ - градусы.

>>nichols(W);

>>ngrid

По этой диаграмме можно определить показатель колебательности.

Рис. 8.6. Диаграмма Никольса

Получение передаточной функции замкнутой системы.

Исследуем влияние обратной связи на динамику САР. Передаточная функция замкнутой системы gos определяется через передаточную функцию

53

разомкнутой системы W(S) при отрицательной обратной связи в соответствии с выражением:

В Matlab это выражение реализуется с помощью функции feedback(W), которая

внашем случае имеет вид:

>>gos=feedback (W, [1])

Transfer function: 8400 s^2 + 28 s + 0.5

-----------------------

67200 s^2 + 168 s + 0.5

Определение нулей и полюсов передаточной функции замкнутой системы

ирасположение их на комплексной плоскости.

>>po=pole(gos)

po =

-0.0012 + 0.0024i -0.0012 - 0.0024i

>>zo=zero(gos) zo =

-0.0017 + 0.0075i -0.0017 - 0.0075i

>>pzmap(gos)

Из (рис. 8.7.) видно, что корни (нули и полюса) характеристического уравнения расположены в левой полуплоскости. Следовательно, замкнутая система автоматического регулирования является устойчивой.

54

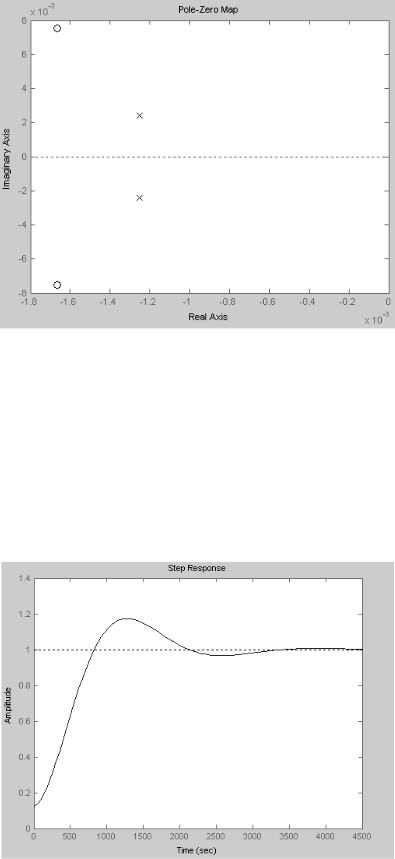
Рис. 8.7. Нули и полюса замкнутой системы

Переходный процесс замкнутой САР с жесткой отрицательной обратной связью.

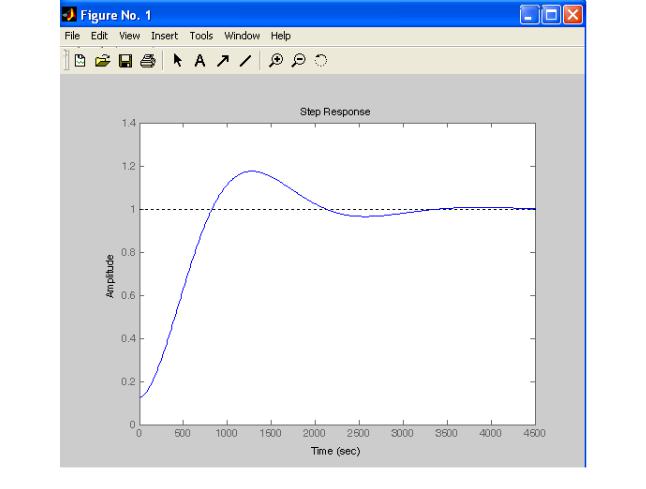
График переходного процесса получаем после реализации функции >> step (gos)

Из графика (рис. 8.8.) видим, что длительность переходного процесса 3500 сек. величина перерегулирования 1,2.

Рис. 8.7. Качество переходного процесса

55

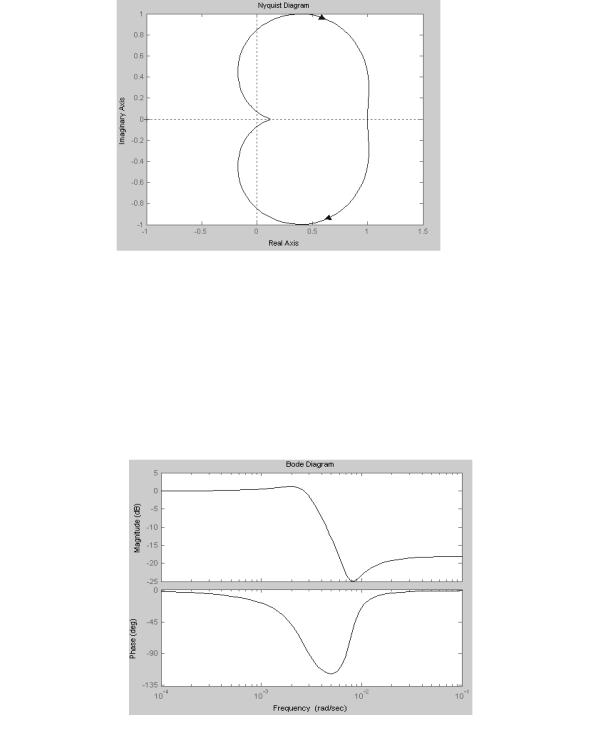
Амплитудно – фазовая частотная характеристика замкнутой САР.

Амплитудно – фазовую характеристику называют диаграммой Найквиста. Она применяется для анализа устойчивости по критерию Найквиста (рис. 8.9.).

>> nyquist (gos)

Рис. 8.9. АФХ замкнутой САР

Частотная характеристика.

Амплитудно – частотная и фазочастотная характеристики строятся с помощью функции bode( ), полученные функции называются функциями Боде. (рис. 8.10.).

>> bode(gos)

Рис. 8.10. Частотная характеристика замкнутой системы

56

Исследование влияние запаздывания на устойчивость и качество переходных процессов.

Введем величину запаздывания в разомкнутую САР τ = x = 2 c. Передаточная функция разомкнутой системы с запаздыванием

WRZ будет иметь вид: Transfer function:

8400 s^4 - 25172 s^3 + 2.512e004 s^2 + 82.5 s + 1.5

---------------------------------------------------

58800 s^4 + 176540 s^3 + 176820 s^2 + 420 s

Полученную передаточную функцию замкнем единичной отрицательной обратной связью gosWRZ = feedback (WRZ, [1]):

Transfer function:

8400 s^4 - 25172 s^3 + 2.512e004 s^2 + 82.5 s + 1.5

------------------------------------------------------

67200 s^4 + 151368 s^3 + 2.019e005 s^2 + 502.5 s + 1.5

Построим переходный процесс замкнутой САР с запаздыванием:

Рис. 8.11. График переходного процесса замкнутой САР с запаздыванием

57

Содержание отчета

1.Получить передаточную функцию разомкнутой системы

2.Получить передаточную функцию замкнутой системы.

3.Определить полюса и нули передаточных функций.

4.Построить графики переходных функций.

5.Построить логарифмические частотные характеристики.

6.Построить частотный годограф Найквиста для функций.

Практическая работа № 9

АНАЛИЗ И СИНТЕЗ САУ МЕТОДОМ КОРНЕВОГО ГОДОГРАФА.

Ознакомление с методикой построения корневых годографов для анализа и синтеза линейных (линеаризованных) систем автоматического управления.

Постановка задачи

Дана модель разомкнутой системы, записанная в виде отношения произведений типовых звеньев:

Необходимо:

1.Построить корневой годограф.

2.Получить коэффициент усиления Kкр, при котором система находится на границе устойчивости.

3.Вычислить частоту wкр, при которой в системе возникают незатухающие колебания.

4.Нанести на ветви корневого годографа значения полюсов замкнутой системы, соответствующие 0.5.Kкр и 0.25.Kкр.

5.Привести выражение для Wз(s) в виде произведения типовых звеньев. Указать значения параметров типовых звеньев.

Вряде случаев, имеющих практическое значение, модель линейной системы автоматического управления (САУ) задается в виде структурной схемы, состоящей из типовых звеньев, математическое описание которых задано в операторной форме. Связь между входом и выходом системы задается

58

в виде передаточной функции W(s). B общем виде передаточную функцию W(s) можно представить в виде:

где s – комплексная переменная, B(s) – полином степени m; A(s) – полином степени n.

Применение метода корневого годографа (КГ) обусловлено фундаментальной зависимостью поведения линейной САУ от полюсов и нулей ее передаточной функции. Под полюсами подразумеваются корни полинома ─ знаменателя A(s), а под нулями ─ корни полинома числителя B(s). Полином A(s) называется также характеристическим многочленом передаточной функции W(s).

Положение полюсов W(s) на комплексной плоскости определяет устойчивость САУ, а в совокупности с нулями вид импульсной переходной функции w(t) и переходной функции h(t).

Метод корневого годографа позволяет находить полюса и нули передаточной функции замкнутой системы, располагая полюсами и нулями разомкнутой системы при изменении коэффициента усиления разомкнутой системы k. Метод корневого годографа является также методом проектирования пропорционального устойчивого регулятора.

Передаточную функцию разомкнутой системы Wp(s) представим в виде:

где s0j – нули передаточной функции Wp(s); si* – полюса передаточной функции

Wp(s), n и m – порядки знаменателя и числителя; K - коэффициент усиления разомкнутой системы; C - коэффициент представления.

Передаточная функция разомкнутой системы, как правило, задается в виде отношения произведений передаточных функций стандартных (типовых) звеньев, при описании которых используются выражения трех видов:

59