asu1

необходимые нам формулы, рабочий лист в Excel примет вид, приведенный на (рис. 7.3.). Теперь построим по полученным средним значениям график.

Рис. 7.2. Транспонированное поле корреляции

Рис. 7.3. Ввод текстовых констант

Последовательно выполняем операции:

«Мастер диаграмм – Графики – График с маркерами, помечающими точки с данных – Далее – Диапазон, указываем =Лист1!$B$12:$I$12 (рис. 7.3.) – Далее

– Поместить на отдельном листе - Готово. В мастере диаграмм можно настраивать вид графика, переключением по вкладкам, выбирая различные параметры.

40

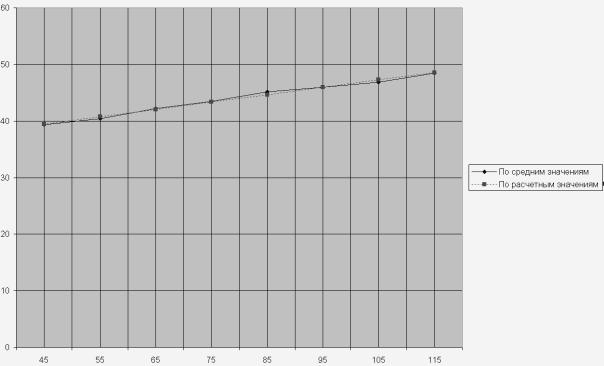
Рис. 7.4. Эмпирическая регрессия

На отдельном листе получится график (его нужно предоставить преподавателю), он показывает, как с увеличением ξ 1 в среднем изменяется Q. Большим доверием будут пользоваться те точки линии, которые принадлежат интервалам с большим количеством наблюдений. С ростом количества наблюдений эмпирическая линия регрессии будет освобождаться от случайных зигзагов, принимая все более правильный, закономерный вид (рис.7.4.).

3. В зависимости от сложности исследуемого объекта в качестве аппроксимирующих уравнений могут быть выбраны различные классы функций оного и многих переменных: степенные многочлены, экспоненциальные и тригонометрические многочлены. В данной конкретной задаче рассмотрим прямолинейную регрессию. Если характер уравнения отличается от прямолинейного, необходимо подобрать его тип. Q = a0 + a1ξ1 , где Q – аппроксимируемая величина; a – коэффициенты многочлена; ξ1 – переменный параметр. Среди наиболее точных методов отыскания коэффициентов многочлена, является метод наименьших квадратов. Сущность метода заключается в следующем. Если для каждого фиксированного значения ξ величина Q нормально распределена, то сумма квадратов отклонений табличных значений Q от вычисленных по формуле приведенной выше, должна быть наименьшей. Как известно, минимум функции можно найти, приравняв нулю частные производные по каждому аргументу. Запишем решение в готовом виде:

41

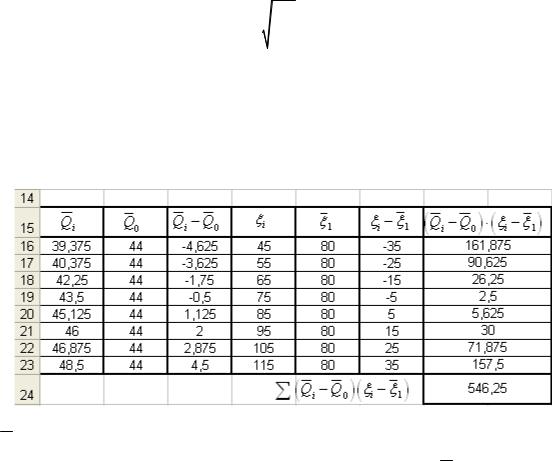
4. Для расчета значений создадим еще одну таблицу (табл. 7.3). Она будет иметь вид:

Таблица 7.3.

Расчет значений

5.Qi взяты из предыдущих расчетов.

6.В ячейки В16 рассчитано среднее значение Qi , по формуле

=СРЗНАЧ($A$16:$A$23). Воспользовавшись маркером заполнения до ячейки В23 получен столбец с данными.

7.В ячейки С16 пишем =A16-B16. Воспользовавшись маркером заполнения до ячейки С23 получен столбец с данными.

8.В ячейки D16 – занесены данные измеряемого диапазона т.е ξ i.

Воспользовавшись маркером заполнения до ячейки D23 получен столбец с данными.

9. В ячейки E16 рассчитано среднее значение.

10.В ячейки F16 пишем =D16-E16. Воспользовавшись маркером заполнения до ячейки F23, получен столбец с данными.

11.В ячейки G16 пишем =C16*F16. Воспользовавшись маркером заполнения до ячейки G23, получен столбец с данными.

12.В ячейки G24 пишем =СУММ(G16:G23).

42

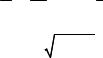
13. Произведем расчет дисперсий. Для этого в ячейке В27 напишем формулу для расчетов =СУММКВРАЗН(A16:A23;B16:B23)/7, основываясь на:

14.

произвести самостоятельно и занести в ячейку D27

15.Взять корни квадратные из значений в ячейках B27 и D27. Занеся соответственно формулы в ячейки В29,D29: =КОРЕНЬ(B27), =КОРЕНЬ(D27)

16.В ячейки В34 самостоятельно рассчитать значение коэффициента корреляции по формуле:

m

∑(Qi − Qo ) (ξ1ι − ξ1 )

Поскольку в нашем случае исследуемая корреляционная зависимость носит линейный характер, в качестве измерителя тесноты связи рассмотрим коэффициент корреляции RQξ1 , определяемый по формуле (7.7). Случай

линейной корреляционной зависимости является наиболее распространенным в практических исследованиях. Это объясняется двумя причинами: вычисление всех параметров линейной связи значительно проще, а получаемые результаты допускают надежную интерпретацию; согласно технологическим ограничениям, параметры объекта могут изменяться в сравнительно узких пределах, и на этих участках криволинейные зависимости могут быть с достаточной точностью аппроксимированы прямолинейными зависимостями.

Теснота связи определяет силу, с которой найденная зависимость проявляется среди многообразных нарушающих ее воздействий. Чем теснее связь, тем точнее по данным значениям аргументов можно предсказать значение функции.

Значения RQξ1 лежат в пределах 0 ≤ RQξ ≤1. Если RQξ1 =1, то связь является

функциональной, то есть учтены все параметры, от которых в той или иной мере зависит Q. Если RQξ1 = 0 , то корреляционная зависимость между

исследуемыми параметрами отсутствует. Если же 0 ≤ RQξ1 ≤1, то говорят о наличии более или менее тесной корреляционной зависимости. Физический

43

смысл коэффициента корреляции таков: он показывает, какая часть полной колеблемости параметров RQξ1 обусловлена изменением аргументов,

охваченных данным уравнением. Коэффициент корреляции RQξ1 практически является измерителем тесноты полученной связи.

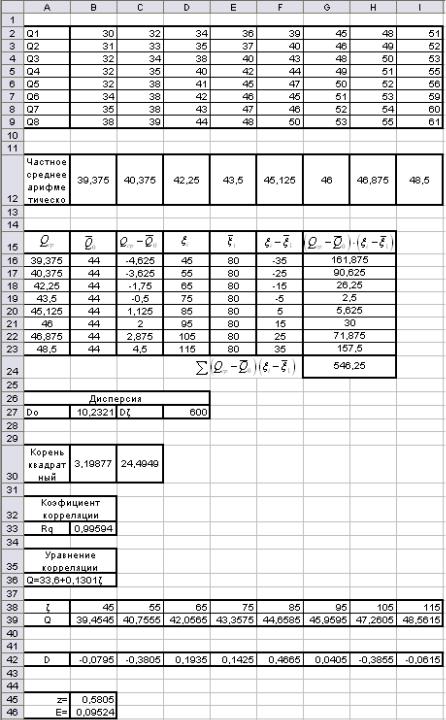
17.В результате всех проведенных вычислений получим вид (табл. 7.4).

18.Самостоятельно составить формулу корреляции:

Втаблице она записана в ячейке А36.

19.По полученной формуле построить график (рис. 7.4.). Определить погрешность интерполяции необходимо:

1.Вычислить разность векторов D = Qср-Q. В ячейку B42=B12-B39, Воспользовавшись маркером заполнения до ячейки I42, получен столбец с данными.

2.Находим скалярное произведение разности векторов z =D·D. В ячейку B45 напишем формулу для расчетов =СУММСУММКВ(B42:I42;B43:I43). В

ячейках B43:I43 записаны нули для того что бы правильно использовать формулу =СУММСУММКВ (массив x; массив y) в Excel.

3. Вычисляем абсолютную среднеквадратическую погрешность:

Для этого в ячейку B48 напишем формулу для расчетов =КОРЕНЬ(B45)/СЧЁТ(B42:I42).

E= 0,095239. (табл. 7.5).

Таблица 7.5

Погрешность интерполяции

Содержание отчета

1.Записать выбранные графические значения.

2.Получить передаточную функцию.

44

Контрольные вопросы

3.Что определяет корреляция случайных величин?

4.В каком диапазоне изменяется коэффициент корреляции?

Таблица 7.4

Окончательный вид

45

Практическая работа № 8

АНАЛИЗ И СИНТЕЗ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ.

Качество работы любой системы управления, в конечном счете, определяется величиной ошибки, равной разности между требуемым и действительным значениями управляемой величины: x(t) = g(t) – y(t).

Знание мгновенного значения ошибки в течение всего времени работы управляемого объекта позволяет наиболее полно судить о свойствах системы управления. Однако в действительности вследствие случайности задающего и возмущающего воздействий такой подход не может быть реализован. Поэтому приходится оценивать качество системы по некоторым ее свойствам, проявляющимся при различных типовых воздействиях. Для определения качественных показателей системы в этом случае используются так называемые критерии качества. Все их можно разбить на четыре группы.

Кпервой группе относятся критерии, в той или иной степени, использующие для оценки качества величину ошибки в различных типовых режимах. Эту группу назовем критериями точности систем управления.

Ко второй группе относятся критерии, определяющие величину запаса устойчивости, т. е. критерии, устанавливающие, насколько далеко от границы устойчивости находится система. Почти всегда опасной для системы является колебательная граница устойчивости. Это определяется тем, что стремление повысить коэффициент передачи разомкнутой системы, как правило, приводит

кприближению замкнутой системы именно к колебательной границе устойчивости и затем — к возникновению незатухающих колебаний.

Третья группа критериев качества определяет так называемое быстродействие систем управления. Под быстродействием понимается быстрота реагирования системы на появление задающих и возмущающих воздействий. Наиболее просто быстродействие может оцениваться по времени затухания переходного процесса системы.

Кчетвертой группе критериев качества относятся комплексные критерии, дающие оценку некоторых обобщенных свойств, которые могут учитывать точность, запас устойчивости и быстродействие.

При рассмотрении понятий запаса устойчивости и быстродействия можно исходить из двух существующих в настоящее время точек зрения.

Во-первых, можно основываться на характере протекания процессов во времени и использовать для формирования критериев качества переходную или весовую функцию, расположение полюсов и нулей передаточной функции замкнутой системы и т. п.

Во-вторых, можно основываться на некоторых частотных свойствах рассматриваемой системы, характеризующих ее поведение в установившемся

46

режиме при действии на входе гармонического сигнала. К ним относятся полоса пропускания, относительная высота резонансного пика и др.

Оба эти подхода имеют в настоящее время большое распространение и используются параллельно. И тот и другой подход требует изучения условий эксплуатации уже построенных систем автоматического управления, так как только на основании такого изучения можно правильно сформулировать количественные оценки, которые могут быть использованы в практике проектирования и расчета новых систем.

Функции Matlab для создания передаточных функций и звеньев.

Функция имеет вид: tf(n,m)

где:

n – вектор коэффициентов числителя передаточной функции. m– вектор коэффициентов знаменателя передаточной функции.

Она служит для образования передаточной функцией звеньев и системы в целом.

Пример

Необходимо образовать передаточную функцию

В нашем случае векторы коэффициентов числителя и знаменателя передаточной функции имеют вид: n = [2, 5] , m = [1, 0, 2, 1].

Ноль в векторе m ставиться потому, что в знаменателе передаточной функции член s2 отсутствует.

Процедуры образования передаточной функции G(s) имеют вид:

>>n = [2, 5];

>>m = [1, 0, 2, 1];

>>gs = tf (n, m)

После нажатия клавиши <Enter> на экране появиться передаточная функция в виде:

47

Transfer function: 2 s + 5

-------------

s^3 + 2 s + 1

Функцию gs = tf (n, m) можно также представить в следующем виде: >> gs = tf ([2 5], [1 0 2 1])

Числа в векторах n и m отделяются друг от друга либо запятыми, либо пробелами ( как в нашем примере), а сами векторы заканчиваются символом (;). Символ точка с запятой подавляет вывод на экран векторов при нажатии клавиши <Enter>.

Функция вида eτ в Matlabe записывается через ряд Паде т.е

Transfer function: s^2 - 3 s + 3

-------------

s^2 + 3 s + 3

Постановка задачи

В качестве объекта исследования выступают линейные (линеаризованные) динамические стационарные системы управления с одним входом и одним выходом. При этом модель одномерной САУ задана в виде комплексной передаточной функции, записанной как отношение полиномов

Необходимо:

1.Получить передаточную функцию разомкнутой системы.

2.Получить передаточную функцию замкнутой системы.

3.Определить полюса и нули передаточных функции.

48

4.Построить графики переходной функции.

5.Построить логарифмические частотные характеристики.

6.Построить частотный годограф Найквиста.

Методический пример

Пусть необходимо исследовать САУ с передаточной функция разомкнутой системы (рис. 8.1.):

Рис. 8.1. Структурная схема разомкнутой САР

49