Установочная лекция к первой контрольной по тау

1. Разложение функции в ряд Тейлора

В технических системах могут быть выделены отдельные устройства, называемые «узлами», имеющие один вход и один выход. Примером такого узла является какой-либо усилитель (электронный, гидравлический, электромашинный и т.д.). Статическая характеристика усилителя – это зависимость выходного сигнала от входного, которую снимают при медленном изменении входной величины, чтобы исключить переходные процессы. Статические характеристики могут быть линейными или нелинейными. Для линейных систем разработана достаточно общая теория, а что касается нелинейных систем, то такой общей теории не существует. Поэтому нелинейные статические характеристики во многих случаях заменяют линейными, которые не слишком сильно отличаются от истинной характеристики только вблизи «рабочей точки». Процесс называется линеаризацией и справедлив, очевидно, для малых по величине входных сигналов. В основе процесса линеаризации лежит формула Тейлора, позволяющая гладкую функцию разложить в степенной ряд:

(1.1)

Доказательство формулы Тейлора.

Пусть функция представлена в виде степенного ряда:

(1.2)

Берем от этого ряда производные:

(1.3)

………………………………….

Подставляем в (1.2) и (1.3) x=0. В результате получаем формулы для коэффициентов степенного ряда:

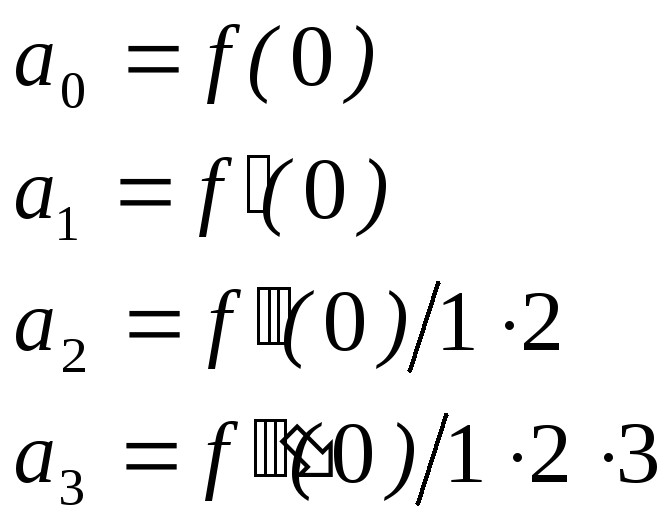(1.4)

что и требовалось доказать.

Любой коэффициент ряда Тейлора можно определить по формуле:

, (1.5)

где предполагается, что факториал нуля равен 1: 0!=1.

Степенной ряд Тейлора в общем виде.

Если рабочая точка находится при x=a, то разложение функции в степенной ряд можно осуществить по формуле:

(1.6)

Именно это соотношение используется при линеаризации, когда нелинейная характеристика заменяется двумя первыми членами ряда Тейлора (1.6).

Разложение в ряд Тейлора некоторых основных функций (доказать самостоятельно):

(1.7)

(1.8)

(1.9)

Эти формулы программно реализованы в вычислительных устройства для определения значений трансцендентных функций. В следующем разделе соотношения (1.7 – 1.9) будут использованы для вывода формулы Эйлера.

2. Теория комплексных чисел.

В основе теории линейных систем в автоматике, электротехнике, радиоэлектронике лежит арифметика комплексных чисел. Потребность в комплексных числах возникает при решении алгебраического квадратного уравнения:

(2.1)

Корнями полинома называются такие значения аргумента х, при которых полином принимает нулевые значения. Корни для уравнения (2.1) находят по формуле:

(2.2)

Если выражение под знаком квадратного корня отрицательно, то говорят, что действительных корней у квадратного полинома нет. Однако, эту информацию нужно каким-то образом зафиксировать. Поэтому была введена мнимая единица:

(2.3)

Выражение (2.2) приобрело следующий вид:

(2.4)

Определение комплексно – сопряженных чисел. Это два числа, у которых действительные части (В) равны, а мнимые части (С) отличаются знаком. Из выражения (2.4) следует, что корни квадратного уравнения комплексно-сопряженны: , где надстрочная звездочка обозначает, что над числом ₁ произведена операция комплексного сопряжения, т.е. перед символами мнимой единицы изменен знак на обратный. Следует отметить, что операция комплексного сопряжения всегда легко выполнима, что и объясняет широкое использование комплексно-сопряженных чисел.

2.1. Формула Эйлера – основное соотношение в теории комплексных чисел

Эта формула имеет следующий вид:

(2.5)

Доказательство

Возьмем ряд для экспоненты (1.7) и подставим в него в качестве аргумента x=j. Воспользуемся также очевидными соотношениями:

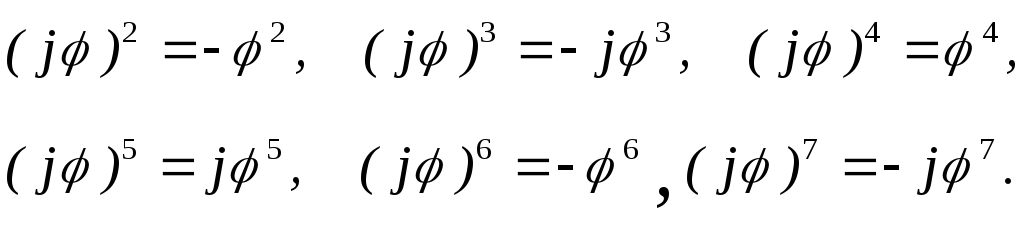(2.6)

В итоге получаем следующее соотношение:

(2.7)

Соберем вместе действительную и мнимую часть:

(2.8)

Сравнивая соотношение (2.8) с рядами Тейлора (1.8) и (1.9), можно заметить, что в действительной части находится косинус, а в мнимой – синус. Таким образом, формулу Эйлера (2.5) можно считать доказанной.

2.2. Представление комплексных чисел.

а) Алгебраическое представление комплексных чисел:

, (2.9)

где введены общепринятые обозначения ReD – действительная (реальная) часть комплексного числа D, ImD- мнимая часть числа D.

b) Геометрическое представление комплексного числа.

Рассмотрим так называемую комплексную плоскость (рис.1).

Р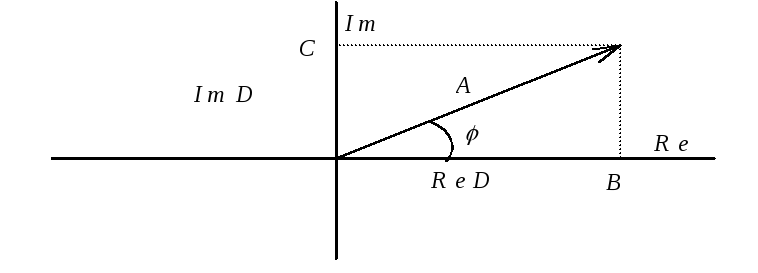ис.1. Изображение комплексного числа на комплексной плоскости в виде вектора.

По оси абсцисс откладывается реальная часть комплексного числа, а по оси ординат – мнимая часть числа. Таким образом, любому комплексному числу можно сопоставить вектор на комплексной плоскости. Суммирование и вычитание комплексных чисел производится также, как и суммирование и вычитание векторов.

c) Тригонометрическое представление комплексных чисел.

Из рис.1 следует, что комплексное число можно задавать другим способом. За основу можно взять длину вектора А, которую называют модулем комплексного числа, и угол  - называемый фазой комплексного числа. В этом случае: Таким образом, основная формула тригонометрического представления приобретает следующий вид:

(2.10)

в) Экспоненциальное представление комплексного числа.

Если воспользоваться формулой Эйлера (2.5), то соотношение (2.10) значительно упрощается, а именно, приобретает следующий вид:

(2.11)

Это представление отличается крайней компактностью и является основным в любых теориях, где используются комплексные числа.

2.3. Перечисленные выше представления являются как бы элементарными видами комплексных чисел. На практике же приходится иметь дело со сложными формулами, в которых могут присутствовать несколько мнимых единиц в разных позициях, в том числе и в качестве аргумента трансцендентных функций. Ниже будут приведены правила, помогающие преобразованию сложной комплексной функции к одному из представлений, прежде всего к алгебраической и экспоненциальной формам.

Определение действительной и мнимой части комплексного числа.

Пусть D =B+jC – комплексное число, для которого несложно получить комплексно сопряженное число: D^=B-jC. Если теперь мы просуммируем эти два соотношения, то мнимая часть сократится и будет получено выражение для действительной части:

(2.12)

Если же произвести вычитание, то сократится действительная часть, что позволяет определить мнимую часть числа:

(2.13)

Из (2.12) и (2.13) и формулы Эйлера (2.5) несложно получить следующие важные соотношения:

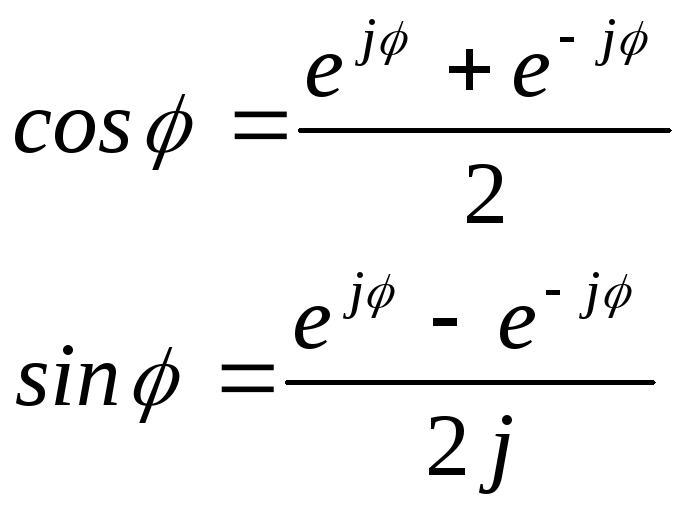(2.14)

Эти формулы можно рассматривать, как алгебраическое определение тригонометрических функций, справедливое не только для действительных углов, но также и для мнимых. Попробуйте самостоятельно доказать следующее – косинус мнимого угла всегда больше 1.

Определение модуля комплексного числа.

Запишем комплексное число и комплексно-сопряженное число в экспоненциальной форме:

(2.15)

При перемножении этих двух формул показатели экспонент в правой части будут складываться:

Таким образом, мы получаем простую формулу для нахождения модуля комплексного числа:

(2.16)

Из рисунка 1, воспользовавшись теоремой Пифагора, можно получить еще один вариант этой формулы:

(2.17)

Нахождение фазы комплексного числа.

Такую формулу легко получить из рис.1:

(2.18)

Примеры использования арифметики комплексных чисел.

Главное достоинство этой арифметики в том, что она сводит тригонометрические вычисления к алгебраическим вычислениям, поскольку благодаря формуле Эйлера все тригонометрические функции могут быть выражены в виде набора экспонент. При этом известные формулы, имеющие весьма громоздкие геометрические или тригонометрические выводы, при использовании комплексных чисел доказываются буквально в несколько строк.

Пример 1.

Получите известное выражение для sin(₁+₂) и cos(₁+₂).

Решение

Запишем формулу Эйлера для трех случаев:

(2.19)

Подставим два последних соотношения в первое вместо экспонент, расположенных в центральной части:

После приравнивания поотдельности вещественной и мнимой частей, получим искомые соотношения:

(2.20)

Пример 2.

Докажите теорему Пифагора, основываясь на формуле Эйлера.

Решение.

Теорему Пифагора можно записать в виде известного тригонометрического соотношения:

. (2.21)

Эту формулу приведем к более удобном виду:

(2.22)

Формула Эйлера позволяет выражение (2.22) существенно упростить:

.

Легко заметить, что мы получили тождество, что и доказывает справедливость теоремы Пифагора.

Пример 3

Решите уравнение:

Это уравнение обычно обескураживает человека, не знакомого с комплексными числами. Школьное утверждение о том, что , основано на геометрическом определении косинуса (отношение прилежащего катета к гипотенузе). Однако теперь мы вправе воспользоваться более общим определением (2.14), что позволяет записать данное уравнение в следующем виде:

Введем обозначение: .Уравнение приобретает следующий вид:

. Становится очевидным, что это квадратное уравнение:

, имеющее два вещественных корня: .

Теперь возвращаемся к переменной х:

Таким образом, данное уравнение имеет два чисто мнимых корня. Здесь мы сталкиваемся с мнимым углом поворота, который, на первый взгляд, кажется чисто математической абстракцией. Однако, в физике известны соотношения, которые можно интерпретировать, как поворот на мнимый угол. Наиболее известным примером являются преобразования Лоренца в специальной теории относительности, которые Минковский проинтерпретировал, как поворот 4-х мерного пространства – времени. Вместе с тем расчеты показали, что угол поворота – мнимый.

Комплексные колебания

Гармонические колебания обычно записывают в виде синусоиды или косинусоиды:

(2.23)

где А – амплитуда колебания, _о - начальная фаза колебания,  - частота, t – время.

Однако использование тригонометрических функций сильно затрудняет, или делает невозможным, проведение расчетов. Поэтому колебательный процесс гораздо удобнее записывать в экспоненциальной форме:

. (2.24)

Геометрическая интерпретация соотношения (2.24)

Р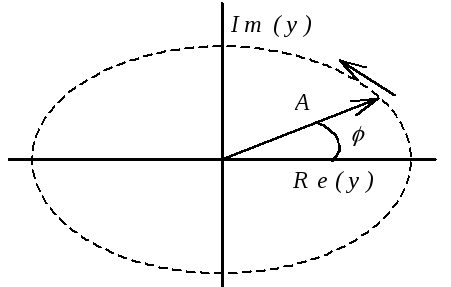ис.2. На комплексной плоскости изображен вектор (2.24). Длина вектора не зависит от времени, однако фаза имеет линейную зависимость: . Это означает, что вектор вращается с постоянной угловой скоростью . Такое вращение называют комплексным колебанием. Конец вектора двигается по окружности против часовой стрелки.

Представление реального колебания в виде комплексного колебания дает следующие преимущества:

1. Колебание описывается вектором на комплексной плоскости с четким изображением мгновенной фазы и мгновенной амплитуды.

2. Приобретают смысл колебания с нулевой и даже отрицательной частотой. Колебания с - это просто неподвижный вектор, ориентированный в комплексной плоскости в соответствии с начальной фазой. Колебание с отрицательной частотой – это вектор, вращающийся по часовой стрелке.

3. Использование комплексных колебаний позволяет наглядно производить суммирование колебаний. В качестве примера рассмотрим задачу, обычно решаемую в курсе общей физики при рассмотрении явления интерференции. Здесь мы её сформулируем несколько по-другому.

Пример 4.

Два источника э.д.с. соединены последовательно, вырабатывают синусоидальные напряжения одинаковой частоты , но разной амплитуды (А₁ А₂ ) и начальной фазы . Требуется заменить два источника э.д.с. одним эквивалентным, определить амплитуду (А) и начальную фазу () вырабатываемого им напряжения.

Суммируемые напряжения запишем в следующем виде:

Эквивалентный генератор будет иметь напряжение той же самой частоты, но существенно другой амплитуды и фазы:

По условию задачи требуется найти А и .

Задачу можно решить двумя способами. Прежде всего перейдем к комплексным колебаниям. В этом случае суммарное комплексное колебание находят путем суммирования двух векторов (рис.3), которые соответствуют колебаниям y₁ и y₂.

Рис.3. Суммирование двух колебаний осуществляется путем суммирования двух векторов на комплексной плоскости.

Таким образом, первый способ решения задачи можно назвать геометрическим. Он сводится к нахождению длины вектора А и угла , опираясь на рис.3 и используя известные формулы, например, закон косинусов. Этот способ хотя и отличается некоторой трудоемкостью, но зато не требует знания комплексных чисел. Именно благодаря этому геометрический метод суммирования колебаний нашел применение в учебниках по общему курсу физики.

Вместе с тем, как уже говорилось выше, теория комплексных чисел позволяет сводить задачи тригонометрии и геометрии к алгебре. Поэтому второй способ суммирования колебаний можно назвать алгебраическим. Он удивительно прост и сводится к тому, что мы суммарное комплексное колебание записываем в виде комплексной функции времени:

Амплитуда равна модулю этого комплексного числа, для нахождения которого необходимо воспользоваться формулой (0), что мы и сделаем:

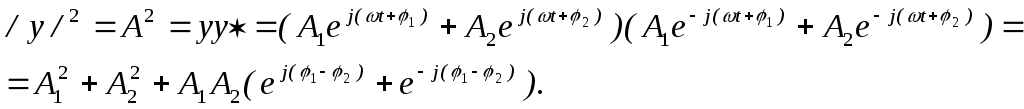
Из соотношения (**) следует, что в скобке находится косинус. Таким образом, окончательное выражение для амплитуды имеет следующий вид:

()

По соотношению ( ) находим начальную фазу суммарного колебания. В этом случае необходимо подставить t=0 и преобразовать соотношение ( ) по формуле Эйлера. В результате можно получить необходимую формулу:

. ()

Как видим, использование комплексных чисел позволяет значительно упростить вычисления, сводя сложные тригонометрические преобразования к более простым алгебраическим.

Разбиение сложной функции в виде дроби с полиномами в числителе и знаменателе на простые дроби.

Такое разбиение часто бывает полезным при интегрировании и решении дифференциальных уравнений. В качестве примера разложим на простые дроби функцию . Прежде всего необходимо найти корни знаменателя (полюса функции). Для этого необходимо решить уравнение:

. Оно имеет три корня: Исходя из теоремы Безу, функцию можно представить в следующем виде:

Разложение на простые дроби проводится методом неопределенных коэффициентов:

Правую часть подводим под общий знаменатель, причем знаменатели в уравнении сразу сокращаются:

Приравниваем коэффициенты при равных степенях p, что дает систему из трех алгебраических уравнений:

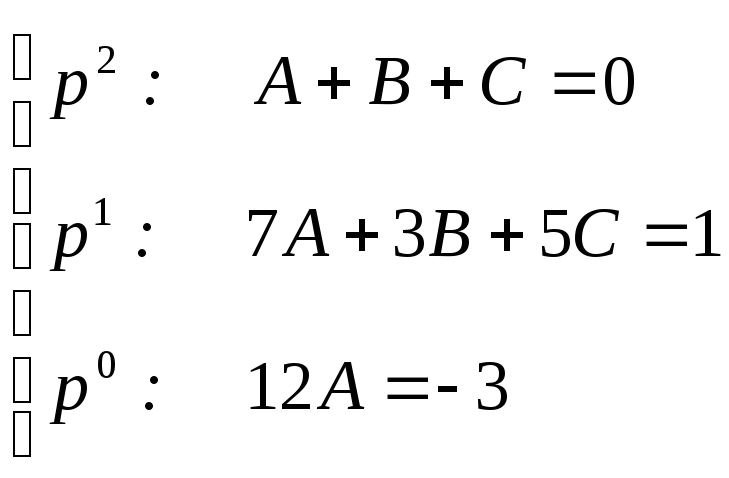
Решение этой системы:

Таким образом, результат разложения функции на простые дроби имеет следующий вид:

Правильность разложения проверяется подведением дробей в правой части под общий знаменатель.