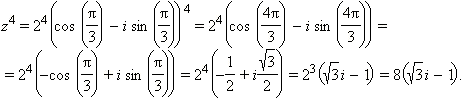1.3.5. Функция feedback ()

Функция feedback () применяется для образования передаточной функции замкнутой системы по известным передаточным функциям разомкнутой системы и цепи обратной связи.

Она имеет вид:

feedback (q, goc, ±)

где;

• goc – передаточная функция цепи обратной связи

• ± – указывает вид обратной связи ( -1 – положительная, + – отрицательная)._

Пример 1.10

Структурная схема системы управления приведена на рис. 2.11.

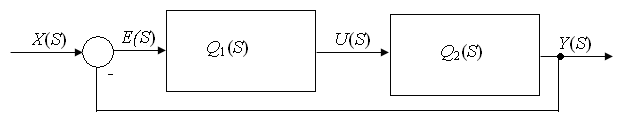
Рис. 2.11. Структурная схема системы управления

Передаточную функции звеньев имеют вид:

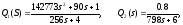
Передаточная функция цепи обратной связи образует отрицательную обратную связь с коэффициентом передачи, равным 1.

Необходимо получить передаточную функцию замкнутой системы управления:

Передаточная функция Q(S) определяется по выражению.

Из этого выражения и структурной схемы видно, что для получе­ния передаточной функции замкнутой системы необходимо вна­чале образовать с помощью функции tf () звенья Q₁(S) и Q₂(S), затем посредством функции series о образовать передаточную функцию разомкнутой системы и после этих процедур использо­вать функцию feedback () для образования передаточной функции замкнутой системы.

>> z1=[142773 90 1]; >> m1=[256 4]; >> q1=tf(z1,m1); >> z2=[0,8]; >> m2=[798 6]; >> q2=tf(z2,m2); >> Q=series(q1,q2) Transfer function: 1.142e006 s^2 + 720 s + 8 ------------------------- 204288 s^2 + 4728 s + 24 >> feedback(Q, [1]) Transfer function: 1.142e006 s^2 + 720 s + 8 --------------------------- 1.346e006 s^2 + 5448 s + 32 >>

Пример 1.11

Структурная схема системы управления приведена на рис. 2.13.

Необходимо получить передаточную функцию замкнутой системы

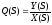
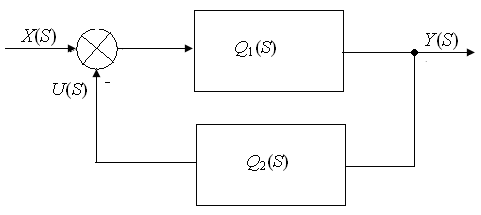
Рис.2.13. Структурная схема системы

с гибкой отрицательной обратной связью

Передаточные функции звеньев имеют вид:

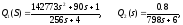
>> z1=[142773 90 1]; >> m1=[256 4]; >> q1=tf(z1,m1); >> z2=[0,8]; >> m2=[798 6]; >> q2=tf(z2,m2); >> feedback(q1,q2,-1) Transfer function: 1.139e008 s^3 + 928458 s^2 + 1338 s + 6 --------------------------------------- 1.346e006 s^2 + 5448 s + 32

Сложение комплексных чиcел

Пример 1

Z1=1+4i, Z2= 4-6i;

Z1+Z2=1+4i+4-6i=5-2i;

Вычитание комплексных чисел

Пример 2

Z1=1+4i, z2=4-6i;

Z1-z2= 1+4i-4-6i=-3-2i;

Умножение комплексных чисел

Пример 3

Построим на комплексной плоскости следующие комплексные числа

Z1=1,Z2=-2 ,,,,,,

Изобразим на комплексной плоскости число . Для определённости и простоты объяснений расположим его в первой координатной четверти, т.е. считаем, что:

Представить в тригонометрической форме комплексные числа: ,,,. Выполним чертёж:

Представить в тригонометрической форме комплексные числа: ,,,.

Деление комплексных чисел

Пример 4

 ,  , а

Пример 5

Дано комплексное число . Записать данное число в алгебраической форме (т.е. в форме).

В знаменателе уже есть , поэтому знаменатель и числитель нужно домножить на сопряженное выражение, то есть на:

Пример 6

Даны два комплексных числа,. Найти их сумму, разность, произведение и частное.

5 + 2i + 2 - 5i = (5 + 2) + (2 - 5)i = 7 - 3i

5 + 2i - (2 - 5i) = (5 - 2) + (2 + 5)i = 3 + 7i

(5 + 2i) · (2 - 5i) = 5·2 - 5·5i + 2·2i - 2·5i² = 10 - 25i + 4i + 10 = 20 - 21i

5 + 2i	=	(5 + 2i)(2 + 5i)	=	5·2 + 5·5i + 2·2i + 2·5i2	=	10 + 25i + 4i - 10	=	29i	=	1i
2 - 5i		(2 - 5i)(2 + 5i)		2·2 + 5·5		4 + 25		29

Изобразим на комплексной плоскости число . Для определённости и простоты объяснений расположим его в первой координатной четверти, т.е. считаем, что:

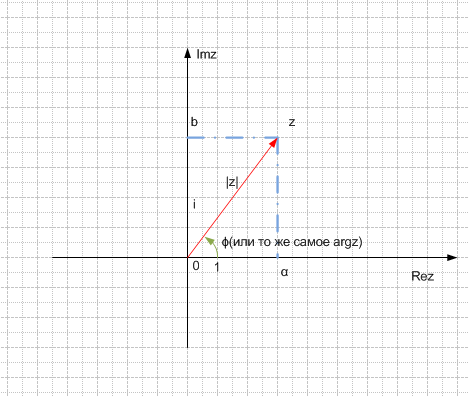
Пример 7

Представить в тригонометрической форме комплексные числа

1)

Найдем модуль и аргумент заданного комплексного числа:

Тогда

2)

аргумент

Отсюда получаем, что

Пример 8

Запишите в тригонометрической форме числа ,,,.

Решение. Находим модуль, аргумент, а затем выписываем тригонометрическую форму:

        

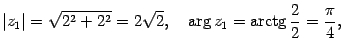
Пусть ,. Найдем произведение:

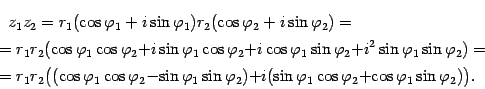
Заметим, что во внутренних скобках стоят формулы косинуса и синуса суммы аргументов. Поэтому

Последняя запись является тригонометрической формой комплексного числа . Значит,

иными словами, при умножении комплексных чисел их модули перемножаются, а аргументы складываются.

Аналогично можно доказать, что

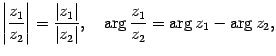
иными словами, при делении комплексных чисел их модули делятся один на другой, а аргументы вычитаются.

Несложно проверить, что если , то

Используя правило умножения комплексных чисел в тригонометрической форме, получим формулу для возведения комплексного числа в степень , где-- натуральное число.

Пусть . Тогда

то есть

Далее находим

то есть

Продолжая умножения дальше, придем к формуле

Эта формула называется формулой Муавра.

Пример 9

Возвести в квадрат комплексное число: z=3+2i

z²=(3+2i)(3+2i)

z²=*(3+2i)²=3²+3*2*2i+(2i)²=9+12i-4=5+12i

Пример 10

Вычислить если 

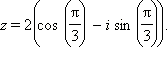 По первой формуле Муавра получаем: 

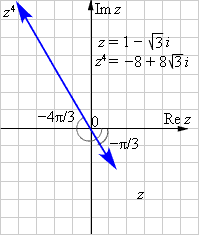
Пример 11

Возвести в степень комплексные числа i⁸,i³¹, (-i)¹⁹

i⁸ = (i²)⁴ = (-1)⁴= 1

i³¹=i*i³⁰=i*(i²)¹⁵=i*(-1)¹⁵=i*(-1)=-i

(-i)¹⁹=(-1)¹⁹*i¹⁹=-i*i¹⁹=-i*(i²)⁹=-i*(-1)⁹=i

Пример 12

Решить уравнение .

Решение. Вычисляем дискриминант 

. Вычисляем корни из дискриминанта по формуле квадратныхкорней из комплексного числа:

.

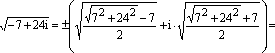
Вычисляем корни уравнения по формуле корней квадратного уравнения:

 или ; .

Ответ: .

Пример 13

разложить трехчлен 2x ² – 4x – 6 на множители первой степени.

 

    Р е ш е н и е .  Во-первых, решим уравнение:  2x ² – 4x – 6 = 0.  Его корни:

                             x₁ = –1  и  x₂ = 3.  Отсюда, 2x ² – 4x – 6 = 2 ( x + 1 ) ( x – 3 ) .

Пример 14

 , если . Представить результат в тригонометрической форме и изобразить его на комплексной плоскости.

Решение: итак, требуется подставить  в «страшную» дробь, провести упрощения, и перевести полученное комплексное числовтригонометрическую форму. Плюс чертёж.

Как лучше оформить решение? С «навороченным» алгебраическим выражением выгоднее разбираться поэтапно. Во-первых, меньше рассеивается внимание, и, во-вторых, если таки задание не зачтут, то будет намного проще отыскать ошибку.

1) Сначала упростим числитель. Подставим в него значение , раскроем скобки и поправим причёску:

В ходе преобразований используются совершенно бесхитростные вещи – правило умножения многочленов и уже ставшее банальным равенство . Главное, быть внимательным и не запутаться в знаках.

2) Теперь на очереди знаменатель. Если , то:

Заметьте, в какой непривычной интерпретации использована формула квадрата суммы . Как вариант, здесь можно выполнить перестановку  под формулу . Результаты, естественно, совпадут.

3) И, наконец, всё выражение. Если , то:

Чтобы избавиться от дроби, умножим числитель и знаменатель на сопряженное знаменателю выражение. При этом в целях применения формулы разности квадратов  следует предварительно (и уже обязательно!) поставить отрицательную действительную часть на 2-ое место: 

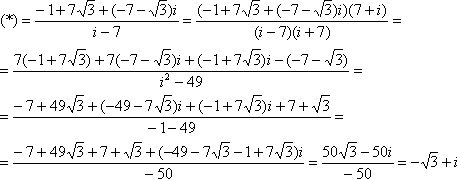
На завершающем шаге произошло хорошее сокращение и это просто отличный признак.

Обозначим наше достижение буквой 

Представим полученный результат в тригонометрической форме. Вообще говоря, здесь можно обойтись без чертежа, но коль скоро, требуется – несколько рациональнее выполнить его прямо сейчас: 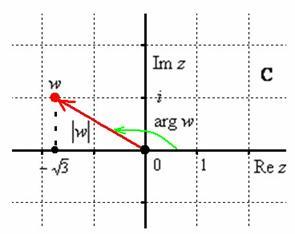Вычислим модуль комплексного числа:

Найдём аргумент. Так как число расположено во 2-й координатной четверти , то:

Угол элементарно проверяется транспортиром. Вот в чём состоит несомненный плюс чертежа.

Таким образом:  – искомое число в тригонометрической форме.

Выполним проверку:  ,

.

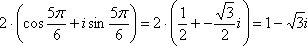Ответ: 

Операции с числами

Ввод действительных чисел

»1.8954896е-12

ans =

1.8955e-012

»

Командное окно

Окно с названием форматов (numericformat)

»1.89547896e-12

ans =

1.895478960000000e-012

»

Результат с форматомLongE

Ввод комплексных чисел

» 2+i*9

ans =

2.000000000000000 + 9.000000000000000i

» y=8+6j

y =

8.000000000000000 + 6.000000000000000i

»

Обозначение мнимой части

Элементарные математические функции

Элементарные действия с комплексными числами

Арифметические действия с комплексными числами

» x=2+i*9; y=8+6j; disp (x+y)

10.00000000000000 + 15.000000000000000i

» disp (x-y)

-6.00000000000000 + 3.000000000000000i

» disp (x*y)

-38.00000000000000 + 84.000000000000000i

» disp (x/y)

0.700000000000000 + 0.600000000000000i

» disp (x\y)

0.823529411764706 -0.705882352941177i

» disp (x^y)

8.612852068220047e+003 – 1.305957650714636e+004i

»

Функции комплексного аргумента

Комплексные числа от элементарных функций

» disp (x*y)

-38.00000000000000 + 84.000000000000000i

» disp (x/y)

0.700000000000000 + 0.600000000000000i

» disp (x\y)

0.823529411764706 - 0.705882352941177i

» disp (x^y)

8.612852068220047e+003 – 1.305957650714636e+004i

» disp (sqrt(-3))

0 + 1.732050807568877i

» disp (abs(x))

9.219544457292887

» disp (exp(y))

2.862227284910554e+003 – 8.329258610593317e+002i

» disp (sin(x))

3.684056738456527e+003 -1.686036345689945e+003i

» disp (sqrt(x))

2.368495773406920 + 1.899940059224610i

»

Комплексные числа от дополнительных функций

» x=2+i*9; y=8+6j;

» disp (real (y))

8

» disp (imag (x))

9

» disp (angle (y))

0.643501108793284

» disp (conj (y))

8.000000000000000 – 6.0000000000000000i

»

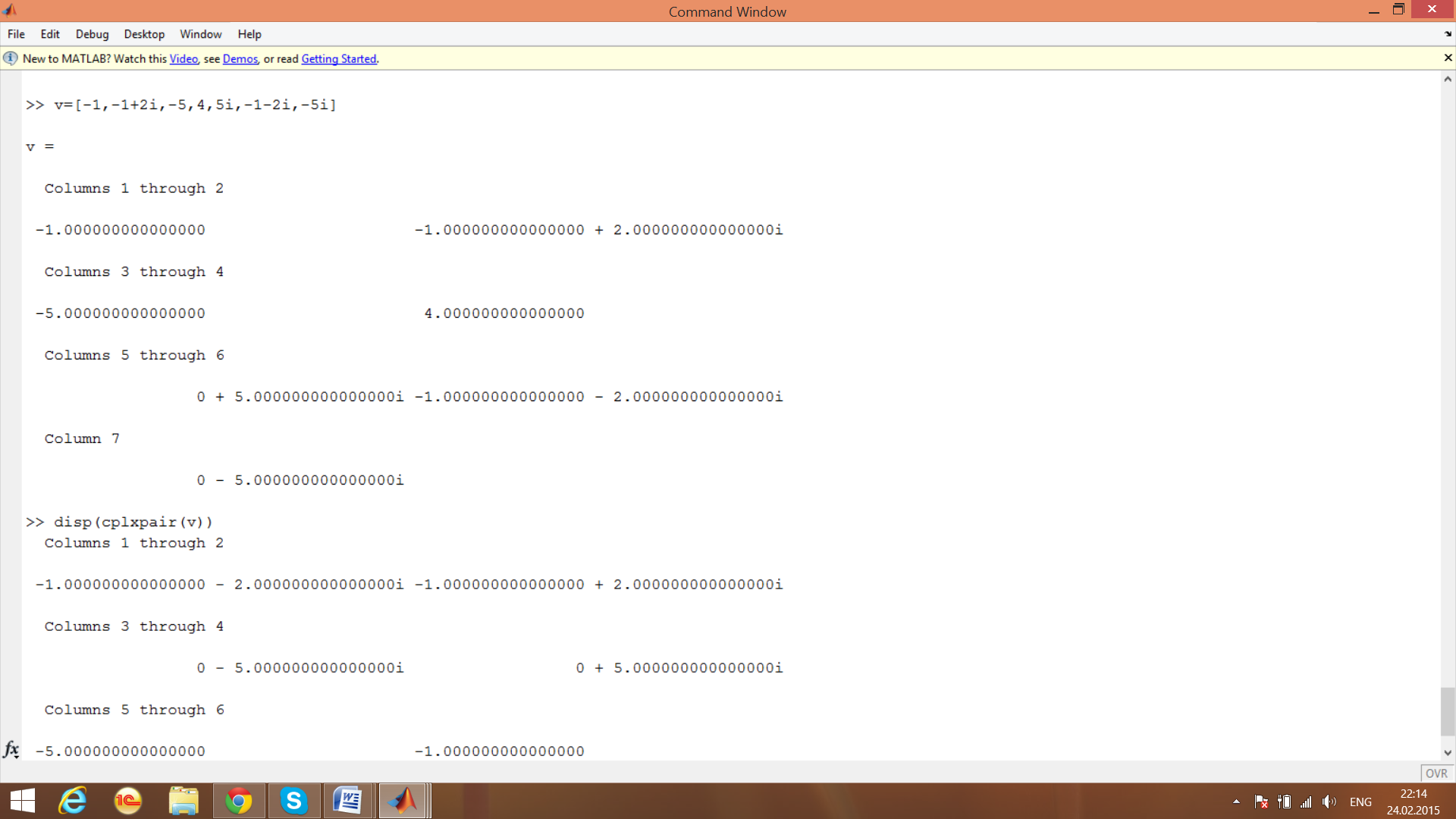
» v=[ -1, -1+2i, -5,4, 5i,-1-2i,-5i]

v =

columns 1 through 2

-1.00000000000000 -1.0000000000000000 + 2.000000000000000i columns 3 through 4

-5.00000000000000 4.0000000000000000

columns 5 through 6

0 + 5.00000000000000i -1.0000000000000000 -2.00000000000000i

column 7

0 - 5.00000000000000i

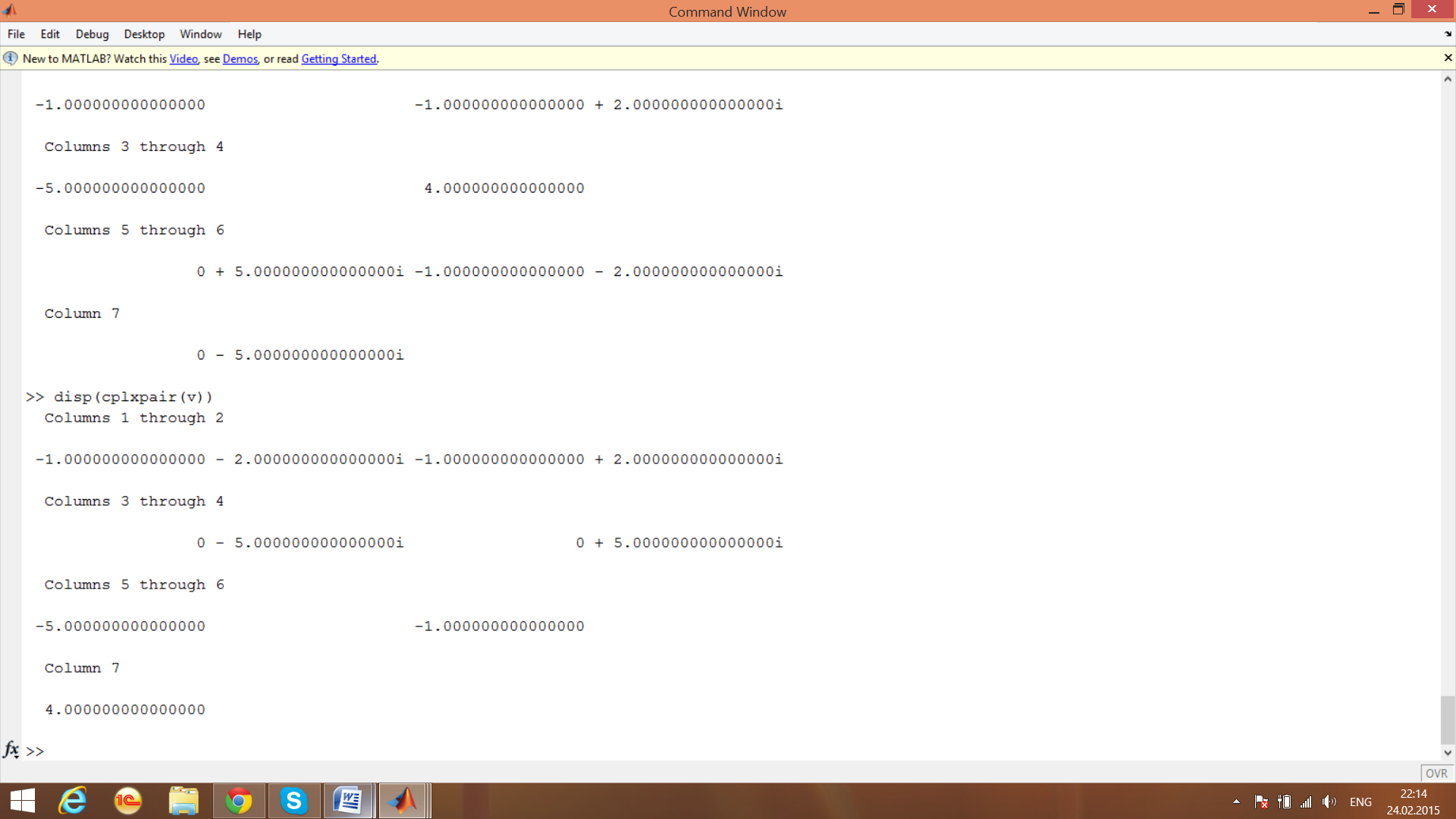
» disp (cplxpair(v))

Columns 3 through 2

-1.000000000000000000 – 2.000000000000000000 -2.0000000000000