КП

Ответ: x = 0.83100433; F(x) = 0.000163.

Задание 4.

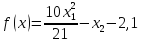
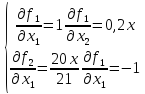
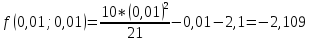
L=1

δ=-0,0899

M=1,008

1,008*1*0,0899*2²=0,36247

Т. к , то метод Ньютона сходится.

Задание 5.

i	0	1	2	3
xi	2,6	3,6	5,6	7,1
yi	68,66	56,55	-51,6	80,65

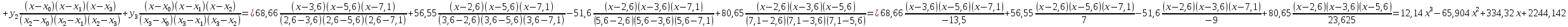
x=68,26

i	0	1	2	3
xi	6,1	10,3	14,5	18,7
yi	87,12	104,95	133,98	149,19

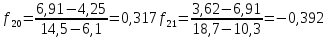
x=99,28

Задание 6.

Табличная зависимость y=F(x)
x	0,1	0,3	0,4	0,6	0,7	0,9
y	-0,1	0,5	0,8	0,7	2,5	2,1

n=6

Задание 7.

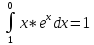
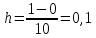
xi	0	0,1	0,2	0,3	0,4	0,5	0,6	0,7	0,8	0,9	1
f(xi)	0	0,112	0,244	0,405	0,597	0,824	1,093	1,410	1,780	2,214	2,718
f(xi+h/2)	0,053	0,174	0,321	0,497	0,706	0,953	1,245	1,588	1,989	2,456	3,001
4f(xi+h/2)	0,210	0,697	1,284	1,987	2,823	3,813	4,980	6,351	7,955	9,826	12,002
fx+h	0,111	0,244	0,405	0,597	0,824	1,093	1,410	1,780	2,214	2,718	3,305

Формула прямоугольников:

Формула трапеций:

N=10

Формула Симпсона:

Формула Ньютона-Котеса:

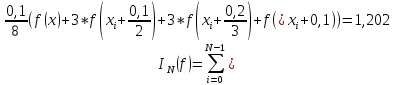
Формула Чебышева:

Формула Гаусса:

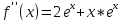
Погрешности:

1. Формула прямоугольников

2. Формула трапеции

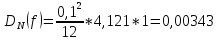
3. Формула Симпсона

Как видно, наиболее точным методом является метод прямоугольников