2.1 Пример

Вариант 3

Шарик, принимаемый за материальную точку, движется из положения внутри трубки, ось которой расположена в вертикальной плоскости.

Найти скорость шарика в положениях В,С и D и давление шарика на стенку желоба в положении С а также сжатие пружины . Трением на криволинейных участках траектории пренебречь .

Исходные данные:

H=3м

Рассматриваем движение точки по отдельным участкам. Так как на участке OACB известно, перемещение точки то будем применять теорему об изменении кинетической энергии, а на участке BD известно время, следовательно будем применять теорему об изменении импульса точки.

Рисунок к варианту 3

Рассмотрим участок OA. Расчётная схема движения точки на этом участке представлена на рисунке 4

Запишем теорему об изменении кинетической энергии согласно формуле (3):

Здесь ,

Тогда

Рассмотрим участок AC. Расчётная схема движения точки на этом участке представлена на рисунке 5

Вычислим

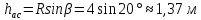
Запишем теорему об изменении кинетической энергии согласно формуле (3):

Здесь ,

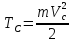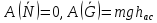
Тогда

Рассмотрим участок CB. Расчётная схема движения точки на этом участке представлена на рисунке 6.

Сначала найдем угол , который равен

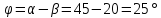
Тогда найдем

Запишем теорему об изменении кинетической энергии согласно формуле (3):

;

Тогда :

Рассмотрим участок BD

Расчётная схема движения точки на этом участке представлена на рисунке 7.

На участке DB в соответствии дано время движения точки следовательно, применяем теорему об изменении импульса .

Проецируем на ось x, направленную по направлению движения в соответствие с рисунком 7, имеем:

С проецируем на ось y.

0=N-G, тогда

Отсюда имеем :

Для определения реакции опоры в положении С используем принцип Даламбера:

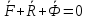(8)

Уравнение (8) выражает принцип Даламбера: для несвободной материальной точки в каждый момент времени сумма активных сил, приложенных к точке, реакций связей и сил инерции равна нулю.

Отметим, что сила инерции всегда направлена в сторону, противоположную ускорению

(9)

Ускорение точки можно разложить на касательное и нормальное ускорение в соответствии. Соответственно силу инерции можно разложить на такие же составляющие:

Касательная сила инерции:

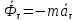
Нормальная или центробежная сила инерции

Для модуля касательной и нормальной сил инерции имеем следующие выражения:

Принцип Даламбера наиболее рационально применять к решению задач динамики, в которых требуется определить реакции связей. В нашей задаче реакцией связи является нормальная реакция поверхности

Рисунок 8 - Расчётная схема для принципа Даламбера.

Проектируем векторное уравнение (8) на нормальную ось n в соответствии с рисунком 8.

N=

Тогда

3. Применение теоремы об изменении кинетической энергии механической системы.

Приращение кинетической энергии системы на конечном участке пути, пройденных точками системы, равно сумме работ внешних и внутренних сил, приложенных к ним на участке пути.

(1)

где -кинетическая энергия системы в начальном и конечном положении;

-суммы работ всех внешних и внутренних сил, приложенных к системе на перемещении системы;

В этой теореме внутренние силы не исключаются в общем случае, но для рассматриваемых неизменяемых систем, состоящих из абсолютно твердых тел, соединенных нерастяжимыми нитями, сумма работ всех внутренних сил равна нулю.

Кинетическая энергия системы равна сумме кинетических энергий всех точке системы

(2)

Кинетическая энергия поступательного движения твердого тела вычисляется так же как и для материальной точки:

(3)

Кинетическая энергия, вращающегося вокруг неподвижной оси, вычисляется по формуле:

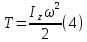
где - момент инерции тела относительно оси вращения, -угловая скорость вращающегося тела.

Кинетическая энергия в плоскопараллельном движении определяется по формуле:

где 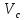– скорость вращения центра масс тела;

-момент инерции тела относительно оси, проходящей через центр масс тела.