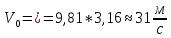- •1.Введение
- •Исходные варианты для выполнения задач по темам:
- •Дифференциальные уравнения движения материальной точки и их интегрирование.
- •Прямолинейное движение точки
- •1.2 Криволинейное движение точки
- •2. Применение общих теорем динамики к исследованию движения материальной точки. Принцип Даламбера
- •2.1 Пример
- •3. Применение теоремы об изменении кинетической энергии механической системы.
- •3.1. Пример 4
- •4. Исследование поступательного, вращательного и плоского движений твердого тела с помощью дифференциальных уравнений.
- •6. Применение уравнения Лагранжа второго рода
- •7.Заключение
Данная
работа выполнена студией потом доделаем.
Наш девиз: Работа не волк в лес не убежит) Наслаждайтесь. А
да в этой нет фоток импровизируй)
МИНОБРНАУКИ РОССИИ
Федеральное государственное бюджетное образовательное учреждение Высшего профессионального образования
«Санкт-Петербургский государственный технологический институт (технический университет)»
УГНС 150000
Направление подготовки 15.03.02 Технологические машины и оборудование
Факультет
Кафедра
Механический
Механики
Учебная дисциплина
Курс 2
Теоретическая механика
Группа 666
КУРСОВАЯ РАБОТА
Тема ДИНАМИКА МАТЕРИАЛЬНОЙ ТОЧКИ И МЕХАНИЧЕСКОЙ СИСТЕМЫ (ваши варианты)
Студент_____________ (фамилия)
______________ (имя)
_______________ (отчество)
Руководитель, _________________________ (подпись, дата)
________________ (инициалы, фамилия)
Оценка за курсовую работу ________________ __________________
(подпись руководителя)
Санкт-Петербург 2999
Содержание
1.Введение…………………………………………………………………………3
2.Интегрирование дифференциальных уравнений движения точки ………...5
2.1. Прямолинейное движение точки ……………………………….……….....6
2.2. Криволинейное движение точки…………………………..………..…….…7
3.Применение основных теорем динамики к исследования движения материальной точки ………………………………………………………….…..9
4. Применение теоремы об изменении кинетической энергии механической
системы …………………………………………………...…………………..…16 5.Исследование поступательного, вращательного и плоскопараллельного движения твердого тела с помощью диф. уравнений……………………...….20
6.Применение уравнения Лагранжа второго рода ……………………………24
7.Заключение ……………………………………………………………………26
1.Введение
Динамика – раздел теоретической механики, рассматривающий движение материальных объектов под действием приложенных сил, то есть устанавливается связь между силой и движением.
Курсовая работа состоит из пяти этапов:
1. Прямолинейное движение материальной точки. В этой задаче применяем основное уравнение динамики:
Криволинейное движение материальной точки. Здесь также применяется основное уравнение динамики.
2. Применение основных теорем динамики к исследованию движения материальной точки. В задаче будем применять теорему об изменения кинетической энергии, теорему об изменении импульс, а также применим принцип Даламбера.
3. Применение теоремы об изменении кинетической энергии механической системы.
4. Исследование поступательного вращательного и плоскопараллельного движения твердого тела с помощью дифференциальных уравнений.
Исходные варианты для выполнения задач по темам:
Прямолинейное движение – вариант №6
Криволинейное движение – вариант №6
Применение общих теорем динамики к исследованию движения материальной точки - вариант №3
Применение теоремы об изменении кинетической энергии механической системы, и исследование поступательного вращательного и плоскопараллельного движения твердого тела с помощью дифференциальных уравнений - вариант №2
Дифференциальные уравнения движения материальной точки и их интегрирование.
Основное уравнение динамики имеет вид:
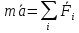 (1)
(1)
где
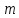 -
масса точки; -ускорение точки;F-
сила.
-
масса точки; -ускорение точки;F-
сила.
Проектируя обе части векторного уравнения на оси x,y,z, получаем дифференциальные уравнения материальной точки:
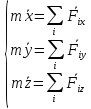 (2)
(2)
Определение движения точки по заданной силе и массе приводит к интегрированию системы дифференциальных уравнений(2)
При решении задач нужно придерживаться следующей последовательности:
1.Выбрать систему координатных осей, введя инерциальную систему отсчета.
2. Составить схему действующих на точку сил, а в случае несвободного движения точки предварительно применить принцип освобождаемости от связей.
3. Установить начальные условия движения точки, т.е выразить t=0
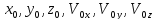 (3)
(3)
4. Составить на основе схемы сил дифференциальные уравнения движения (2).
5. Проинтегрировать полученную систему уравнений, определив постоянные интегрирования из начальных условий(3).
6. Произвести кинематическое исследование полученного решения.
Прямолинейное движение точки
Вариант 6
Условие:
С какой начальной скорость должен
вылететь вертикально вверх снаряд из
зенитного орудия, чтобы подняться на
высоту h=49м,
если не учитывать сопротивление воздуха?
Сколько времени будет проходить подъем?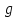 =9,81
=9,81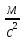
Решение:
Будем рассматривать снаряд как материальную точку, предполагая всю массу его сосредоточенной в его центре тяжести; за ось OY примем прямую, по которой движется точка; за начало координат примем то положение, в котором находилась точка в начальный момент времени.
При
t=0
из условий задачи имеем
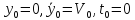 (3)
(3)
41Составим
схему сил в соответствии с рисунком 1,
действующих на снаряд во время полета.
Во время полета на снаряд действует
только сила тяжести
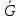 .
.
Составим дифференциальное уравнение
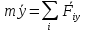
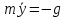 m
m

Проинтегрировав полученное выражение, получим
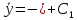 (4)
(4)
При вторичном интегрировании получим
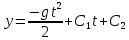 (5)
(5)
Где
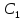 и
и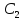 – постоянные интегрирования.
– постоянные интегрирования.
Подставляем начальные условия (3) в полученные зависимости (4) и (5), определяем постоянные интегрирования:
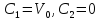
Тогда зависимости (4) и (5) приобретают вид:
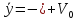 (6)
(6)
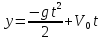 (7)
(7)
Для решения конкретной задачи выписываем конечные условия
при
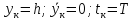
Подставляем конечные условия в зависимости (6) и (7) определяем начальную скорость, на которую поднялся заряд, а так же конечное время.
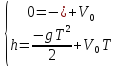
Время
подъема
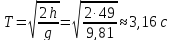
Начальная
скорость