
Индивидуальная практическая работа ИПР3-1
Вариант 15
Задача 1. Исследуйте сходимость числового ряда, применив для этого подходящий признак сходимости
![]() .
.
Решение.
![]() ,
,
![]() .
.
Применим признак Даламбера.
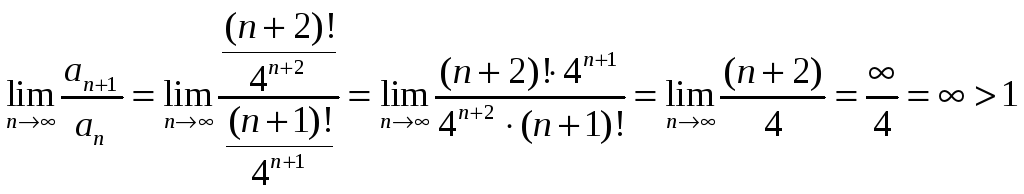
И, следовательно, ряд расходится.
Задача 2. Исследуй сходимость числового ряда, применив для этого подходящий признак сходимости.
![]() .
.
Решение.
Воспользуемся интегральным признаком Коши
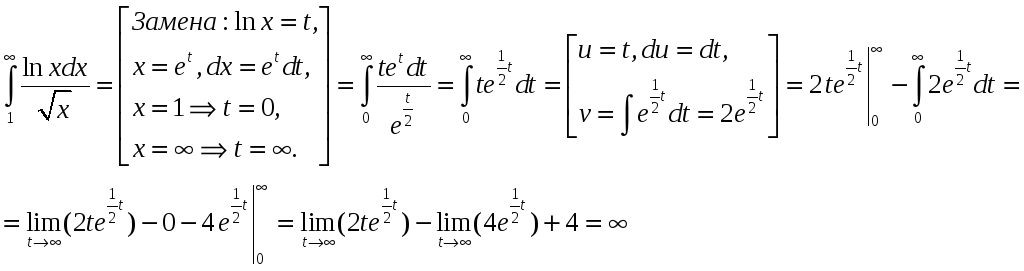 следовательно, ряд расходится.
следовательно, ряд расходится.
Задача 3. Исследуйте сходимость числового ряда, применив для этого подходящий признак сходимости
![]() .
.
Решение.
![]() .
.
Воспользуемся предельным признаком Коши
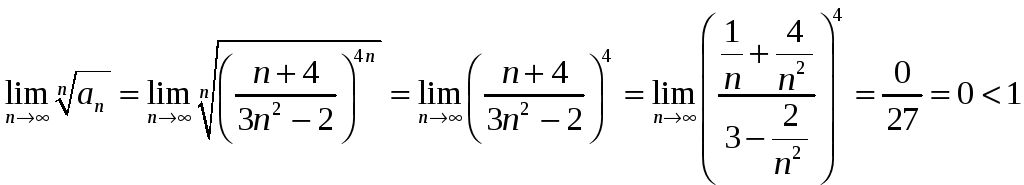 ,
,
следовательно, ряд сходится.
Задача 4. Исследуйте сходимость знакочередующегося ряда. Установите характер сходимости (абсолютная или условная).
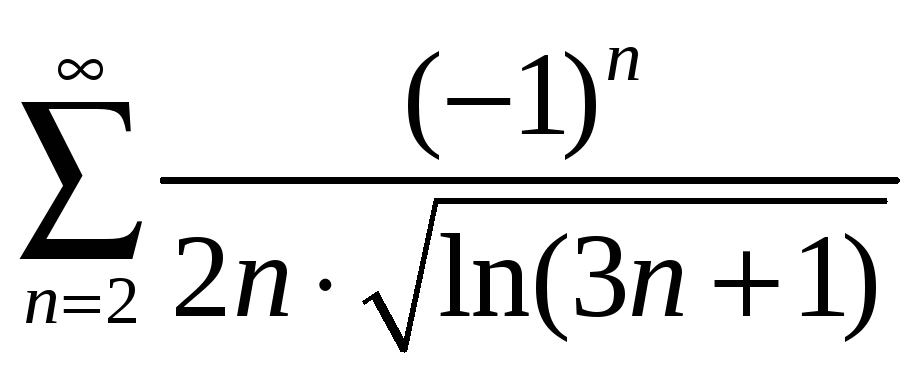 .
.
Решение.
Т.к.
![]() и
и
![]() ,
,
то выполнены условия признака Лейбница, и данный ряд сходится.
Для установления характера сходимости
составим ряд из абсолютных величин,
т.е. ряд
![]() .
.
![]() .
.
Воспользуемся интегральным признаком Коши
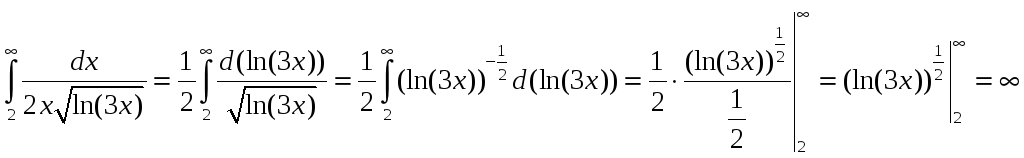 следовательно, ряд расходится. Значит,
и исходный ряд
следовательно, ряд расходится. Значит,
и исходный ряд
![]() расходится. Следовательно, ряд
расходится. Следовательно, ряд
![]() сходится условно.
сходится условно.
Задача 5. Найдите интервал и область сходимости степенного ряда.
![]() .
.
Решение.
Для нахождения области сходимости ряд
воспользуемся признаком Даламбера
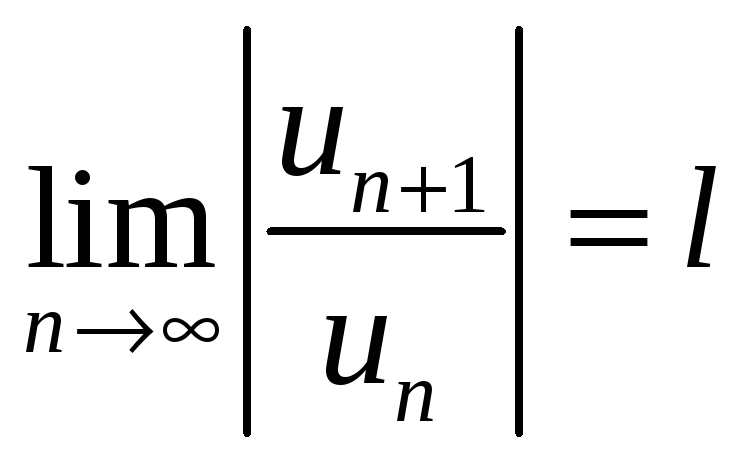 .
.

Ряд сходится при
![]() .
.
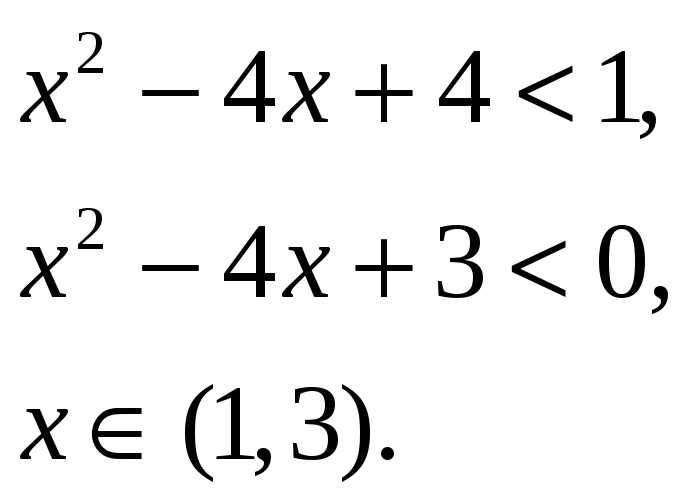
Отсюда интервал сходимости
![]() .
.
Исследуем поведение ряда в точках
![]() и
и
![]() .
.
При
![]() имеем ряд
имеем ряд
![]() .
Воспользуемся признаком Лейбница
.
Воспользуемся признаком Лейбница
![]() и
и
![]() ,
выполнены условия признака и ряд
сходится.
,
выполнены условия признака и ряд
сходится.
При
![]() имеем ряд
имеем ряд
![]() .
.
Воспользуемся признаком сравнения
![]() .
.
Ряд
![]() сходится, следовательно, и ряд
сходится, следовательно, и ряд
![]() - сходится.
- сходится.
Таким образом, областью сходимости ряда
является интервал
![]() .
.
Задача 6. Пользуясь признаком Вейерштрасса, докажите равномерную сходимость данного ряда на указанном промежутке.
![]() ;
;
![]() .
.
Решение.
![]() .
.
Исследуем с помощью признака Даламбера
следующий ряд
![]() .
.
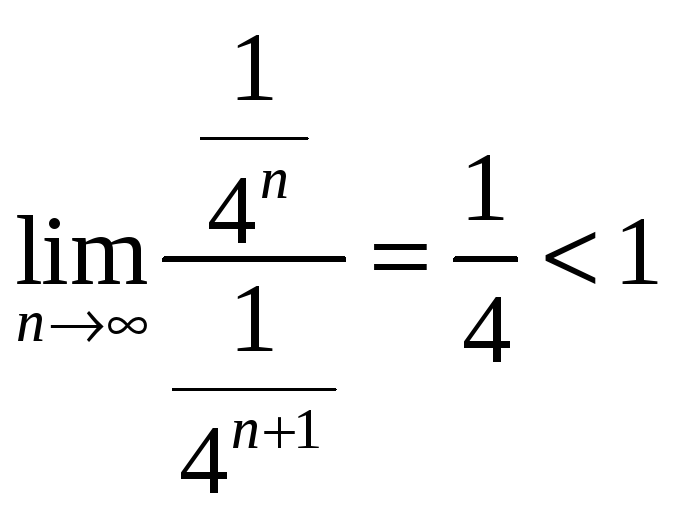 .
.
Следовательно, ряд
![]() сходится. Таким образом, из сходимости
мажорирующего ряда в силу признака
Вейерштрасса следует, что исходный ряд
сходится. Таким образом, из сходимости
мажорирующего ряда в силу признака
Вейерштрасса следует, что исходный ряд
![]() сходится на
сходится на
![]() равномерно.
равномерно.
Задача 7. Разложите функцию
![]() в ряд Тейлора по степеням
в ряд Тейлора по степеням
![]() .
.
![]() ;
;
![]() .
.
Решение.
Ряд Тейлора имеет вид
![]() ,
где
,
где
![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
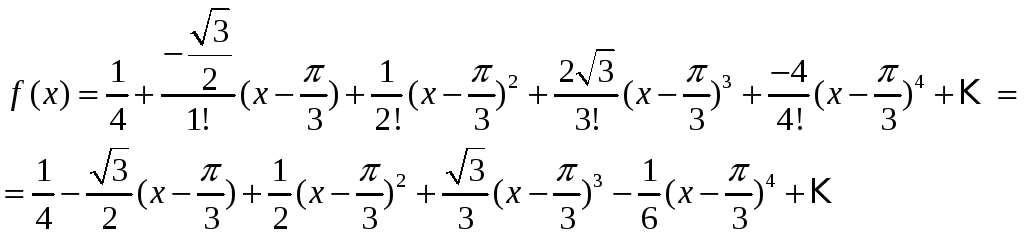
Задача 8. Вычислите интеграл, разложив
подынтегральную функцию в ряд Маклорена.
Укажите количество членов числового
ряда, полученного поле интегрирования
степенного ряда, необходимое для
достижения точности вычислений с
погрешностью
![]() .
.
![]() .
.
Решение.
Разложим подынтегральную функцию
![]()
![]() .
.
Подставляя в интеграл вышеприведенное разложение подынтегральной функции и почленно интегрируя в указанных пределах, получаем
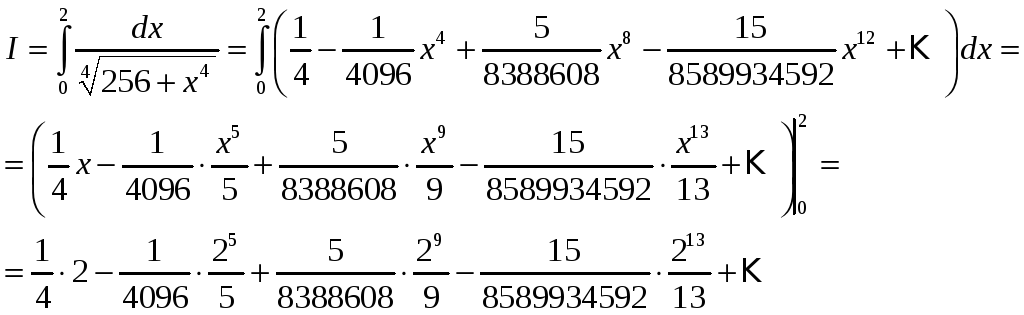
Ряд знакочередующийся. Погрешность
замены суммы ряда суммой его первых
![]() членов по абсолютной величине меньше
первого из отброшенных членов. И поскольку
членов по абсолютной величине меньше
первого из отброшенных членов. И поскольку
![]() ,
то для вычисления приближенного значения
интеграла с требуемой точностью
достаточно взять первые четыре слагаемых.
,
то для вычисления приближенного значения
интеграла с требуемой точностью
достаточно взять первые четыре слагаемых.
![]() .
.
Задача 9. Вычислите предел, используя разложение элементарных функций в ряд Маклорена.
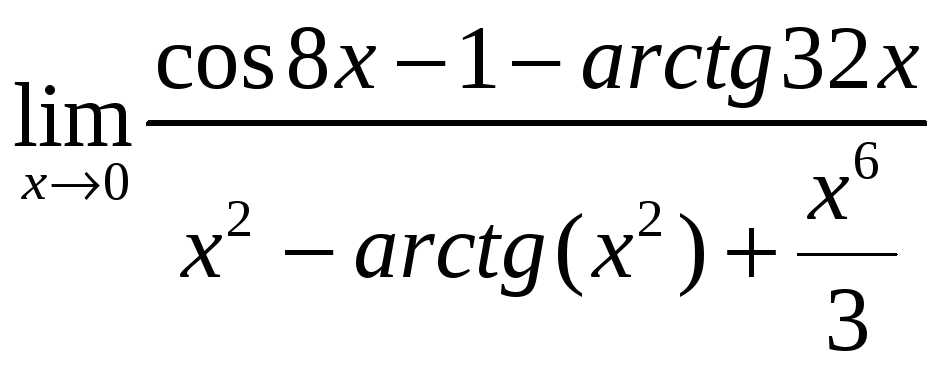 .
.
Решение.
![]() ,
,
![]() ,
,
![]() .
.

Задача 10. Разложите функцию
![]()
в тригонометрический ряд Фурье на
интервале
![]() .
.
Решение.
Запишем функцию следующим образом
![]()
Период в данном случае
![]() ,
полупериод
,
полупериод
![]() .
.
Найдем коэффициенты разложения в ряд Фурье
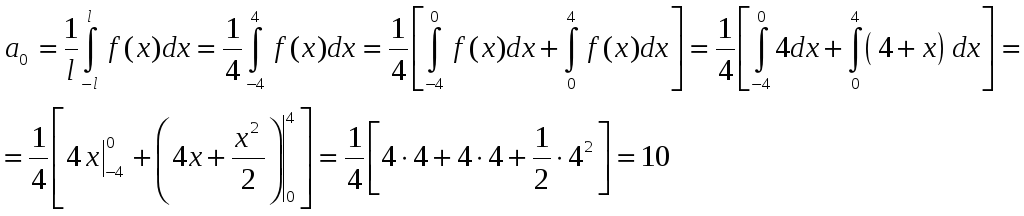
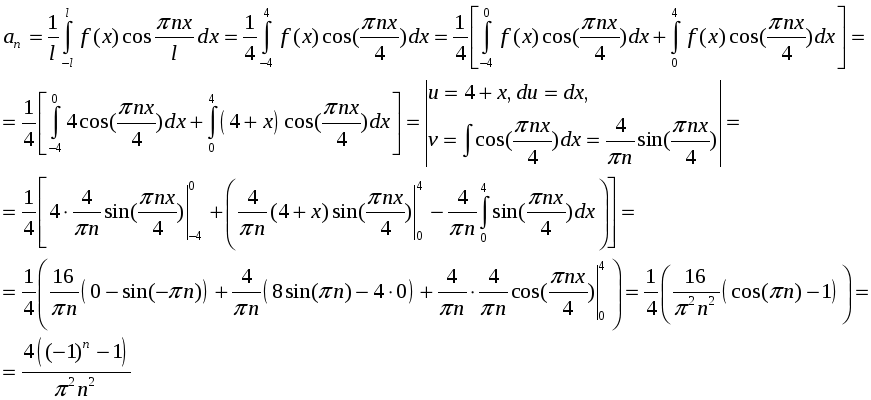
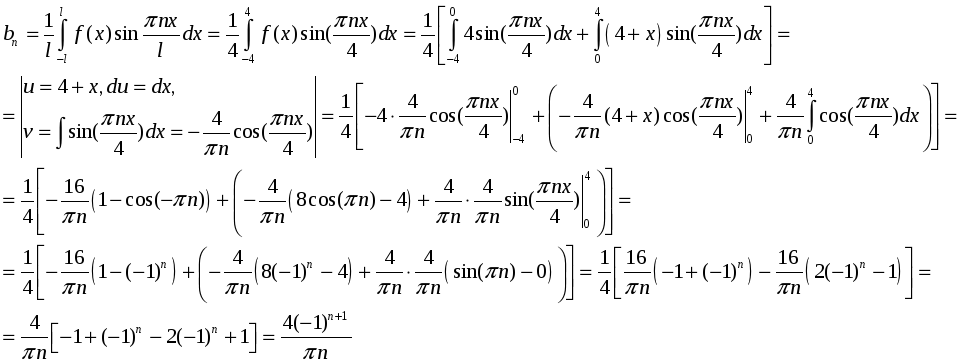
Разложение в тригонометрический ряд Фурье будет следующим
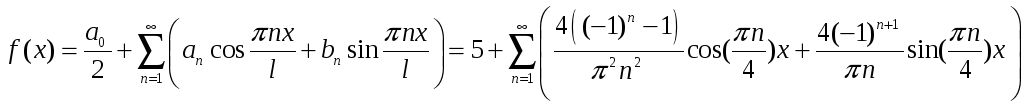
Задача 11. Разложите функцию
![]() в тригонометрический ряд Фурье по
синусам на интервале
в тригонометрический ряд Фурье по
синусам на интервале
![]() .
.
Решение.
Для получения ряда Фурье по синусам,
доопределим функцию на интервале
![]() нечетным образом:
нечетным образом:
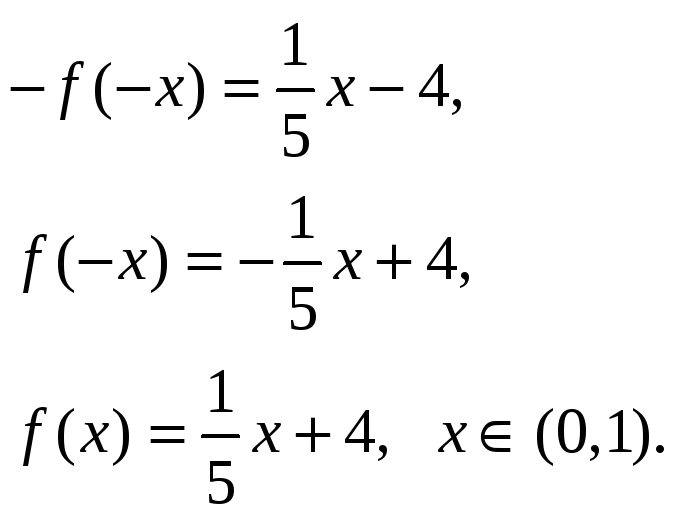
Имеем
![]()
Вычислим коэффициенты Фурье
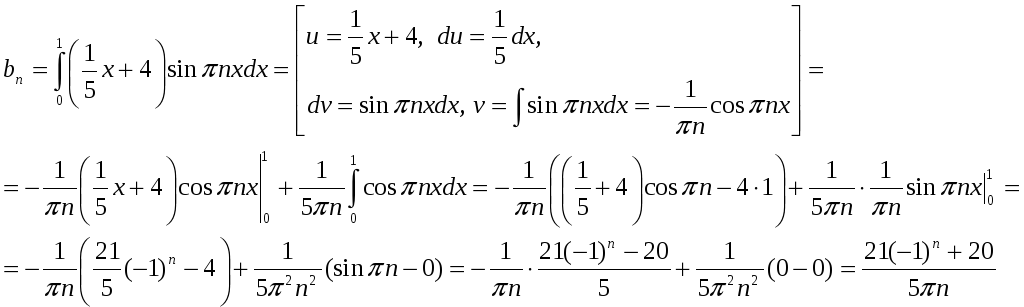 Таким
образом, ряд Фурье по синусам имеет вид
Таким
образом, ряд Фурье по синусам имеет вид
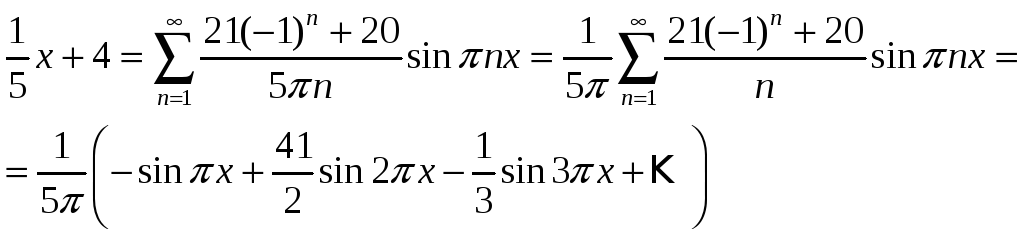
Задача 12. Найдите косинус-преобразование
Фурье
 функции
функции
![]() ,
,
![]() .
.
Решение.
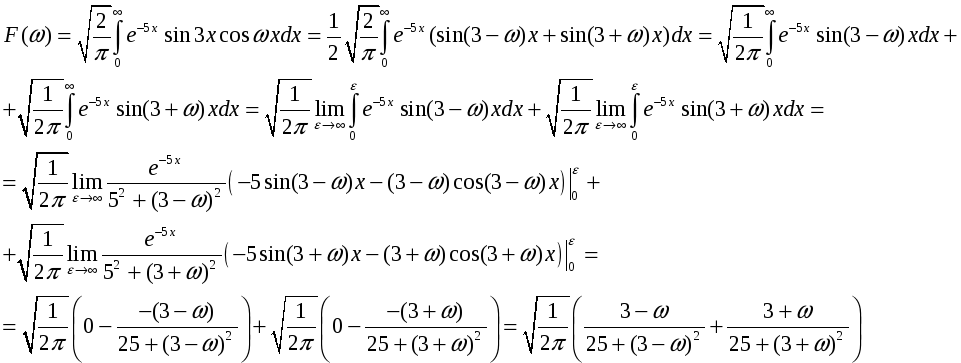
Индивидуальная практическая работа ИПР3-2
Вариант 15
Задача 1. Постройте на комплексной
плоскости область
![]() ,
заданную системой неравенств. Проверьте,
принадлежит ли заданная точка
,
заданную системой неравенств. Проверьте,
принадлежит ли заданная точка
![]() области
области
![]() .
.
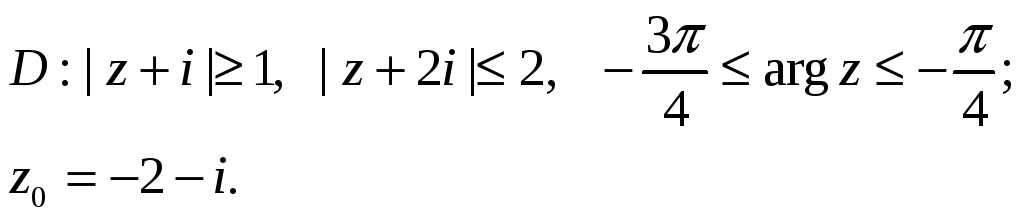
Решение.
Неравенство
![]() соответствует внешней части круга
радиусом
соответствует внешней части круга
радиусом
![]() с центром в точке
с центром в точке
![]() ,
включая ограничивающую его окружность.
,
включая ограничивающую его окружность.
Неравенство
![]() соответствует внутренней части круга
радиусом
соответствует внутренней части круга
радиусом
![]() с центром в точке
с центром в точке
![]() ,
включая ограничивающую его окружность.
,
включая ограничивающую его окружность.
Неравенство
![]() соответствует сектору окружности. На
рисунке представлена область
соответствует сектору окружности. На
рисунке представлена область
![]() .
.

Точка
![]() не принадлежит области
не принадлежит области
![]() .
Проверим это аналитически:
.
Проверим это аналитически:
![]() - неравенство выполнено.
- неравенство выполнено.
![]() -
неравенство не выполнено.
-
неравенство не выполнено.
![]() - неравенство не выполнено.
- неравенство не выполнено.
Значит, точка
![]() не принадлежит области
не принадлежит области
![]() .
.
Задача 2. Определите область (круг)
сходимости данного комплексного ряда.
Исследуйте его сходимость (сходится
абсолютно, сходится условно, расходится)
в точках
![]() ,
,
![]() ,
,
![]() .
.
![]() ;
;
![]() ,
,
![]() ,
,
![]() .
.
Решение.
Применим признак Даламбера:
![]() ,
,
![]() .
.
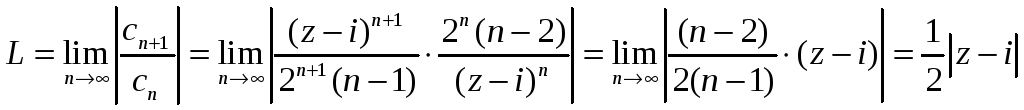
Отсюда, следовательно, ряд сходится при
условии
![]() или внутри круга
или внутри круга
![]() радиусом
радиусом
![]() с центром в точке
с центром в точке
![]() .
.
На рисунке изображены точки, которые необходимо исследовать и область сходимости.
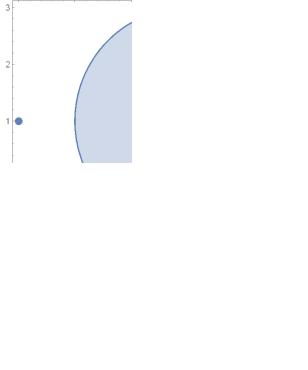
Точка
![]() расположена на границе круга сходимости,
т.к.
расположена на границе круга сходимости,
т.к.
![]() .
Для исследования сходимости заданного
ряда в этой точке подставим её в ряд:
.
Для исследования сходимости заданного
ряда в этой точке подставим её в ряд:
![]() .
.
![]() .
.
Таким образом, исходный ряд сходится
абсолютно в точке
![]() при
при
![]() .
.
Точка
![]() расположена внутри круга сходимости,
т.к.
расположена внутри круга сходимости,
т.к.
![]() ,
поэтому ряд в ней сходится абсолютно.
,
поэтому ряд в ней сходится абсолютно.
Точка
![]() расположена
вне круга сходимости, т.к.
расположена
вне круга сходимости, т.к.
![]() ,
поэтому ряд в ней расходится.
,
поэтому ряд в ней расходится.
Задача 3. Проверьте, является и
функция
![]() аналитической в области
аналитической в области
![]() .
Вычислите интеграл от этой функции по
указанной кривой
.
Вычислите интеграл от этой функции по
указанной кривой
![]() .
.
![]() ;
;
![]() ;
;
![]() – ломаная
– ломаная
![]() :
:
![]() ,
,
![]() ,
,
![]() .
.
Решение.
Для проверки того, является ли функция
аналитической, воспользуемся условиями
Коши-Римана. Для этого с помощью формулы
![]() представим заданную функцию в виде
представим заданную функцию в виде
![]() .
С учетом
.
С учетом
![]() имеем
имеем
![]() откуда получаем
откуда получаем
![]() ,
,
![]() .
.
Найдем частные производные
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Теперь проверим выполнение условия Коши-Римана:
![]() ,
,
![]() .
.
Так как условия Коши-Римана выполняются
для любых
![]() и
и
![]() ,
то функция
,
то функция
![]() является аналитической на всей комплексной
плоскости, включая и область
является аналитической на всей комплексной
плоскости, включая и область
![]() .
.
Теперь вычислим интеграл от заданной функции.
![]()
![]() – ломаная
– ломаная
![]() :
:
![]() ,
,
![]() ,
,
![]() .
.
Заданная кривая
![]() представляет собой ломаную
представляет собой ломаную
![]() :
:
![]() ,
,
![]() ,
,
![]() .
.
В данном случае воспользуемся формулой
![]() .
.
На отрезке
![]() :
:
![]() .
.
На отрезке
![]() :
:
![]() .
.
На отрезке
![]() :
:
![]() .
.
Вычислим интеграл
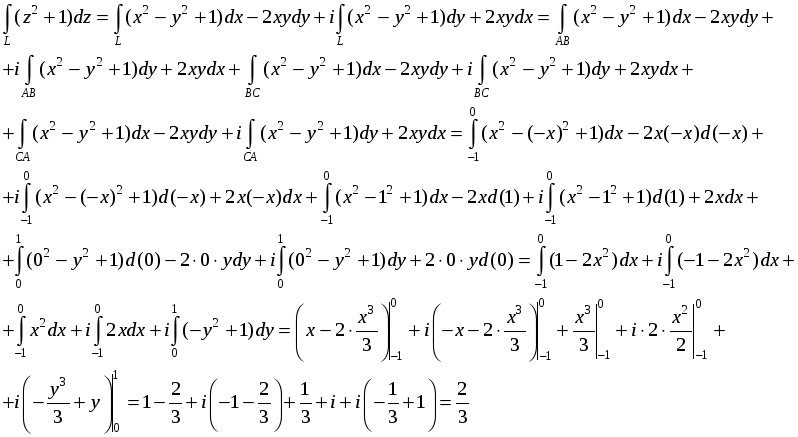
Задача 4. Функция
![]() разложена в ряд Лорана в окрестности
своей изолированной особой точки
разложена в ряд Лорана в окрестности
своей изолированной особой точки
![]() ,
где
,
где
![]() .
.
А) Определите тип особой точки
![]() и найдите в ней вычет функции
и найдите в ней вычет функции
![]() .
.
Б) Вычислите с помощью вычетов интеграл
![]() ,
если
,
если
![]() .
.
![]() ,
,
![]() ;
;
![]() .
.
Решение.
![]()
Т.к. функция
![]() в окрестности изолированной точки
в окрестности изолированной точки
![]() содержит бесконечное число слагаемых
в главной части, то точка
содержит бесконечное число слагаемых
в главной части, то точка
![]() является существенно особой точкой.
является существенно особой точкой.
Вычетом функции
![]() в точке
в точке
![]() называется коэффициент
называется коэффициент
![]() разложения этой функции в ряд Лорана
по степеням
разложения этой функции в ряд Лорана
по степеням
![]() ,
в данном случае
,
в данном случае
![]() ,
значит,
,
значит,
![]() .
.
Рассмотрим интеграл
![]() .
.
![]()
Внутри контура интегрирования
![]() расположена только одна особая точка
подынтегральной функции, которая
согласно ряду Лорана является существенно
особой точкой. Вычет в этой точке равен
расположена только одна особая точка
подынтегральной функции, которая
согласно ряду Лорана является существенно
особой точкой. Вычет в этой точке равен
![]() ,
значит,
,
значит,
![]() .
.
Задача 5. Найдите все лорановские
разложения функции
![]() по степеням
по степеням
![]() .
.
![]() ,
,
![]() .
.
Решение.
Функция
![]() не является аналитической, т.к. имеем
изолированную особую точку
не является аналитической, т.к. имеем
изолированную особую точку
![]() .
Исключим ее из рассмотрения, разбив
комплексную плоскость на две области
.
Исключим ее из рассмотрения, разбив
комплексную плоскость на две области
![]() и
и
![]() окружностью с центром в точке
окружностью с центром в точке
![]() радиусом, равным расстоянию от
радиусом, равным расстоянию от
![]() до особой точки:
до особой точки:
![]() .
.
Найдем
![]() .
.
Таким образом, имеем
![]() ,
,
![]() .
.

Для удобства разложения в ряд Лорана
преобразуем заданную функцию, выделив
явно выражение
![]() :
:
![]()
В области
![]() имеем:
имеем:
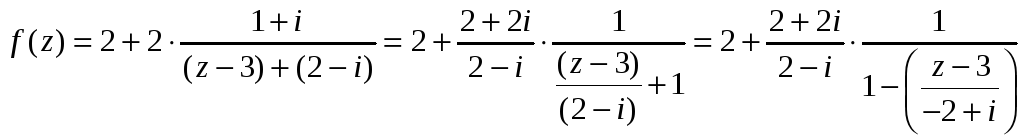 .
.
Воспользуемся формулой суммы бесконечно
убывающей геометрической прогрессии,
в области
![]() выполнено неравенство
выполнено неравенство
![]() ,
значит,
,
значит,
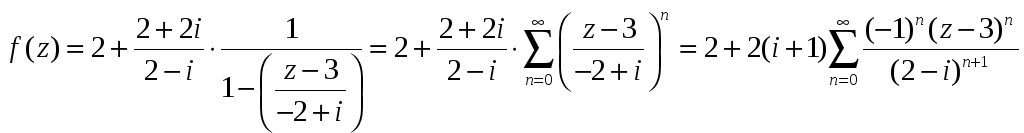 .
.
В области
![]() имеем:
имеем:
 .
.
Воспользуемся формулой суммы бесконечно
убывающей геометрической прогрессии,
в области
![]() выполнено неравенство
выполнено неравенство
![]() ,
значит,
,
значит,
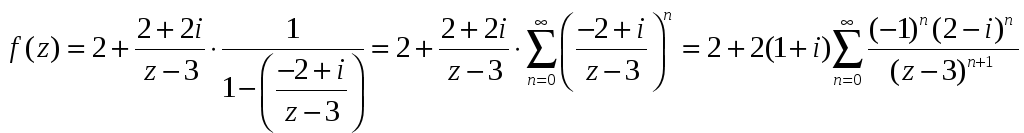 .
.
Таким образом, в разных областях аналитичности функция имеет различные разложения в ряд Лорана.
Задача 6. Дана функция
![]() .
Найдите её изолированную особую точку
.
Найдите её изолированную особую точку
![]() и разложите функцию в ряд Лорана в
окрестности точки
и разложите функцию в ряд Лорана в
окрестности точки
![]() .
С помощью вычетов найдите интегралы
.
С помощью вычетов найдите интегралы
![]() ,
,
![]() ,
,
![]() ,
где
,
где
![]() ,
,
![]() ,
,
![]() – заданные контуры.
– заданные контуры.
![]() ;
;
![]() ,
,
![]() ,
,
![]() .
.
