2.3 Составление математической модели задачи

При разработке математической модели задачи решаются такие вопросы:

выбор параметров управления;
выбор критерия оптимальности;
формирование ограничений и целевой функции в общем виде и с использованием конкретных числовых данных.

Выбор критерия оптимальности в расстановочной задаче существенно зависит от соотношения провозной способности флота П и объема перевозок Q. В курсовой работе ПQ.

Критерий оптимальности – максимум чистой валютной выручки.

F_ij = F_ij -R_ij ( і = 1,m ;j = 1,n)

_F_11
=_{389
– 116,7 = 272,3 тыс. долл. – доход 1 судна на
1 первой схеме движения.}

_{Остальные
показатели сводим в табл. 2.4.}

Таблица 2.4 Доход за рейс, тыс. долл

№судна	Схемы
№судна	1	2	3	4
1. Капитан Кушнаренко	272,3	126	277,2	123,2
2. Ленинская Гвардия	129,5	63	126	67,2
3. Коммунист	261,8	115,5	241,5	112

Математическая модель задачи в общем виде :

Z = F_ij* x_ij– max (4)

q_il* x_ij Q_l (l=1,S) (5)

t_ij* x_ij= T_i (і =1,m) (6)

x_ij 0 ( і = 1,m ; j = 1,n) (7)

где x_ij – число рейсов судов і– го типа на j – ой схеме движения (параметры управления), судо – рейсы ;

T_i - бюджет времени судов і– го типа, судо – сутки.

T_i= N_i*Т_пл(і =1,m), (8)

где N_i – число судов і– го типа;

Т_пл- продолжительность планового периода (Т_пл= 365 сут.);

Т₁= 3*365=1095 (судо –сут.);

Т₂ = 5*365=1825 (судо –сут.);

Т₃ = 5*365=1825 (судо –сут.);

Q_l - количество груза, предъявленное к перевозке на l– ом участке, тыс.т;

G_l- множество схем движения, содержащих l– ый участок;

S – количество груженых участков.

Экономический смысл:

целевой функции (4) – максимизировать чистую валютную выручку.
ограничения (5) отражают требование перевозки груза в количестве, не превышающем заявленного;
ограничения (6) отражают требования использования бюджета времени в эксплуатации судов всех типов на перевозках;
ограничения (7) – условие неотрицательности переменных.

Математическая модель задачи в координатной форме записи:

Z = F₁₁*x₁₁+ F₁₂* x₁₂+ 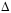F₁₃* x₁₃+F₁₄*x₁₄+F₂₁* x₂₁+F₂₂*x₂₂+F₂₃**x₂₃+F₂₄*x₂₄+F₃₁*x₃₁+ F₃₂* x₃₂+ F₃₃* x₃₃+F₃₄*x₃₄ – max