
- •3. Визначники 2–го порядку та їх властивості.
- •5Формула Крамера для систем лінійних алгебраїчних рівнянь іі і ііі порядків.
- •Доведення:
- •6Означення визначника n-го порядку
- •7Властивості визначників n-го порядку
- •9.Лінійно-незалежні системи векторів. Базис, розклад вектора за базисом.
- •10. Проекція вектора на вісь.
- •11 Декартова система координат
- •Застосовуючи проекції маємо
- •За т.Піфагора маємо
- •14. Мішаний добуток трьох векторів.
- •15. Векторне і нормальне рівняння площини.
- •17. Кут між двома площинами.
- •19. Пряма в просторі
- •20. Кут між прямими в просторі. Умови належності двох прямих одній площині
- •21. Кут між прямою і площиною
- •22. Канонічне рівняння еліпса, його геометричні властивості.
- •23. Канонічне рівняння гіперболи, її геометричні властивості.
- •24. Канонічне рівняння параболи, її геометричні властивості.
- •25. Загальне рівняння кривої другого порядку.
- •26. Види матриць. Лінійні операції над матрицями.
- •27 Множення матриць
- •28 Елементарні перетворення матриць
- •32. Комплексні числа. Тригонометрична форма комплексного числа
- •33. Дії над компл. Числами. Ф-ла Муавра
- •34. Операції над многочленами.
- •35. Корені многочленів. Теорема Безу. Метод Горнера
- •37. Раціональні дроби
- •39. Вимірність і базис векторного простору. Перетворення координат при переході до нового базису.
- •40.Підпростори векторного простору
- •41.Афінний простір...
- •42.Ранг матриці.
- •49.Ортонормовані базиси і ортогональні матриці.
- •50.Ортогональні перетворення.
- •51 Означення квадратичних форм(кф). Основні ознаки додатної визначеності.
- •52 Зведення кф до канонічного вигляду
- •53) Поняття множини. Рівність множин.
- •54) Операції над множинами.
- •55) Означення функції. Види відображень.
- •58. Аксіоми множин дійсних чисел
- •59. Розширення множини дійсних чисел
- •60. Основні характеристики дійсного числа.
- •61. Обмежені та необмежені числові множини.
- •62. Верхня та нижня межа множини.
- •63 Принцип Архімеда.
- •65) Еквівалентність множин та поняття потужності
- •66) Зчисленна потужність
- •67) Континуальна потужність
1.Системою
лінійних рівнянь-
наз. с-ма м
вигляду. (1)
(1)
де х![]() ,
,![]() =
=![]()
![]()
![]()
![]()
Коефіцієнти
при невідомому утв. таблицю, яка наз.
матрицею розміру m![]() n
n
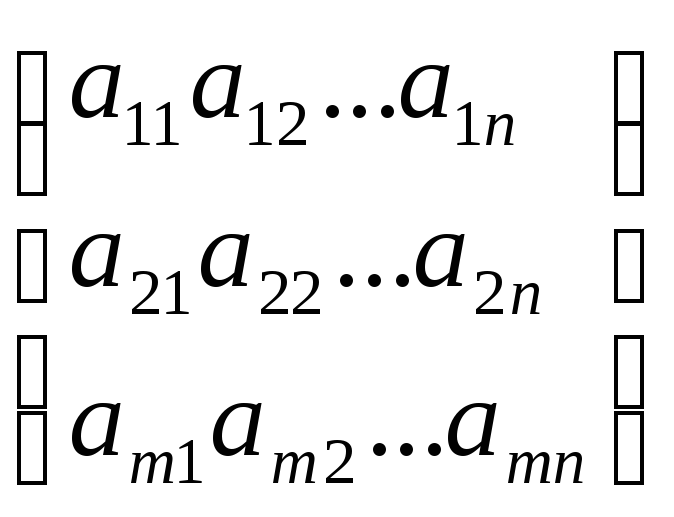 якщо
m=n,
то матриця наз. квадр.
порядку n
якщо
m=n,
то матриця наз. квадр.
порядку n
Одинична матриця- квадр. матр. на головній діагоналі якої стоять 1 решта елем. =0.
Змінні і вільні члени можна пред. у вигляді таких матриць

Розв’язок
СЛР- наз.
така сукупність чисел
![]() ,
які перетворюють кожне з рівнянь системи
в тотожність.
,
які перетворюють кожне з рівнянь системи
в тотожність.
Якщо СЛР має розв.- наз. сумісною, якщо ні- то несумісна.
Якщо СЛР має єдиний розв’язок- визначена, якщо більше- невизначена.
Зауваження:
 другого
порядку
другого
порядку
2СЛР- наз. еквівалентними, якщо ці системи мають одну й ту саму множ. розв’яз. або вони одночасно несумісні.
Елементарні перетворення СЛР-такі перетворення + до обох частин деякого рівняння с-ми іншого рівняння множ. на деяке число.
Переставлення двох будь-яких рівнянь, множення деякого р-ня на число, яке не =0, видалення з сист. рівняння вигляду 0=0.
Доведення:
Нехай до 2-го рів-ня додали 1-ше помнож.
на![]() .
Утв. нове рівняння. НехайL
.
Утв. нове рівняння. НехайL![]() =
=
![]() ,L
,L![]()
![]() -два
рівняння початкової системи. Рівняння
L
-два
рівняння початкової системи. Рівняння
L![]() замінимо на
замінимо на
![]() .
Якщо прав. рівності
.
Якщо прав. рівності![]() іL
іL![]()
![]() поч..
с-ми, то викон. рівності L
поч..
с-ми, то викон. рівності L![]() =
=
![]() і
і
![]() .
навпаки, якщо викон. рівностіL
.
навпаки, якщо викон. рівностіL![]() =
=
![]() і
і
![]() перетворення
с-ми, то правильні рівностіL
перетворення
с-ми, то правильні рівностіL![]() =
=
![]() і L
і L![]()
![]() -початков.
-початков.
2.Метод Гаусса- це спосіб роз. СЛР, що полягає у перетворенні с-ми, у таку еквіваленту, розв. якої знаходь. досить легко.
Нехай в
СЛР (1)
![]()
![]()
Якщо
![]() ,
то шукаємоа
з
номером і,
який не = 0.
,
то шукаємоа
з
номером і,
який не = 0.
переставляємо
місцями відповідні рядки, виключаючи
з усіх рядків с-ми поч. з 2-го, зміну х,
таким
чином множимо перший рядок на
![]() та віднімаємо від
і-го
р-ня,
та віднімаємо від
і-го
р-ня,
![]() одержимо
еквівалентну систему.
одержимо
еквівалентну систему.
Застосовуємо
аналогічні дії для вилуч. змінної
![]() спираючись на 2-ге рівняння . В результаті
перетворень може виник. р-ня
спираючись на 2-ге рівняння . В результаті
перетворень може виник. р-ня![]() ,
то якщо
,
то якщо![]() ,
то р-ня
,
то р-ня
виключаємо
з системи; якщо![]() то система несумічна. Якщо СЛР сумісна,
то метод Гаусса дасть такий результат:
то система несумічна. Якщо СЛР сумісна,
то метод Гаусса дасть такий результат:
 де
де
![]()
![]() ,
якщо було р-ня 0=0);
,
якщо було р-ня 0=0);![]() (якщоk=n,
то сис-ма визначена, бо з останнього
р-ня можна знайти
(якщоk=n,
то сис-ма визначена, бо з останнього
р-ня можна знайти
 ),
а потім знайти решту змінних.
),
а потім знайти решту змінних.
Якщо
![]() ,
то система невизначена, та
,
то система невизначена, та![]() змінних знайдемо через
змінних знайдемо через![]() вільних змінних, тобто безліч розв’язків.
вільних змінних, тобто безліч розв’язків.
Висновок: метод Гауса можна застос. для розв. будь- якої СЛР.
СЛР наз. однорідною, якщо всі вільні члени=0, інакше вони наз. неоднорідними.
Однорідна с-ма завжди сумісна.
3. Визначники 2–го порядку та їх властивості.
Означення :
Визначником 2–го порядку називається число (алгебраїчний вираз), що визначається за таким правилом :
а11 а12
∆=│ а21 а22 │= а11*а22-а12*а21
Властивості визначників 2-го порядку:
1.значення визначника не зміниться при його транспортуванні ( при заміні рядків відповідними стовпчиками і навпаки):
а11 а21
∆т =│ а12 а22│
∆ = ∆т
Наслідок : рядки та стовпці визначника рівноправні, отже всі властивості, які мають місце для рядків, вірні і для стовпців.
2.при переставленні двох рядків (стовпців) визначник змінює знак на протилежний:
∆


 '
=
а11
а12
=
а21
а22
=
(а21*а12
– а11*
а22)
= –∆
'
=
а11
а12
=
а21
а22
=
(а21*а12
– а11*
а22)
= –∆
а21 а22 а11 а12
3.спільний множник всіх елементів деякого рядка (стовпця) можна винести за знак визначника :

 ∆= λа11
λ12
= λа11а22
– λа12а21
=
λ(а11а22
- а12а21
) = λ
∆
∆= λа11
λ12
= λа11а22
– λа12а21
=
λ(а11а22
- а12а21
) = λ
∆
а21 а22
4
 .якщо
у визначнику всі елементи деякого рядка
( стовпця) є сумами двох доданків, то цей
визначник дорівнює сумі двох визначників,
що відрізняються від заданого вибраним
рядком, а саме : у першого цей рядок
складається з перших доданків, а у
другого – з других.
.якщо
у визначнику всі елементи деякого рядка
( стовпця) є сумами двох доданків, то цей
визначник дорівнює сумі двох визначників,
що відрізняються від заданого вибраним
рядком, а саме : у першого цей рядок
складається з перших доданків, а у
другого – з других.
∆ = а111+а1111 а112+а1112 =а22* ( а111 + а1111) – а21* (а112 + а1112)
а21 а22






∆ = а111+а1111 а112+а1112 = а111а112 + а1111 а1112 = а22 х
а21 а22 а21 а22 а21 а22
х(а111 + а1111) – а21 ( а112 + а1112)
5.визначник дорівнює нулю при виконанні однієї з наступних умов:
1)всі елементи деякого рядка (стовпця) дорівнюють нулю;
2)всі елементи деякого рядка (стовпця) пропорційні відповідним елементам іншого рядка ( ст.)
∆
 =
а
в = 2ав-2ав = 0
=
а
в = 2ав-2ав = 0
2а 2в

 3)якщо є два однакових
рядки ( стовпці)
3)якщо є два однакових
рядки ( стовпці)
∆ = а в = ав – ав =0
а в
6.визначник не змінить свого значення, якщо до елементів деякого рядка ( ст.) додати відповідні елементи іншого рядка ( ст. ), домноженого на деяке число.
а




 11
а12+λа11
а11
а12
а11
λа11
а11
а11
11
а12+λа11
а11
а12
а11
λа11
а11
а11
а21 а22+λа21 = а21 а22 + а21 λа21 = ∆ + λ│а21 а21│= ∆
4.Визначник 3-го порядку. Алгебраїчні доповнення та мінори. Формула Лапласа.Означення :
Визначником ( детермінантом) 3-го порядку називається число ( алгебраїчний вираз ), що визначається за правилом

 а11
а12
а13
а11
а12
а13
∆ = а21 а22 а23 = а11а22а33+а12а23а31+а21а32а13-а31а22а13-а21а12а33-а11а32а23
а31 а32 а33
Зауваження: означення визначника 3-го порядку виписується за допомогою правила трикутників.
Зауваження : визначник можна обчислити за правилом Сарюса:








 а11
а12
а13
а11
а12
а13
а11
а12
а11
а12
а13
а11
а12
а13
а11
а12
∆ = а21
а22
а23
= а21
а22
а23
21
а22
= а21
а22
а23
= а21
а22
а23
21
а22
а31 а32 а33 а31 а32 а33 а31 а32
Властивості 1-6 визначника 2-го порядку мають місце і для визначника 3-го порядку.
Властивість 7(формула Лапласа) : визначник дорівнює сумі добутків елементів будь-якого рядка (ст.) на відповідні цим елементам алгебраїчні доповнення:
∆ = аі1Аі1 + аі2Аі2 + аі3Аі3; і= 1,3
∆ = а1jA1j + a2jA2j + a3jA3j; j =1,3.
Властивість 8: сума добутків елементів будь-якого рядка (ст.) на алгебраїчні доповнення відповідних елементів іншого рядка (ст.) дорівнює нулю.
∆ = а11А11+ а12А12 + а13А13
0=а11А21+а12А22+а13А23
Метод нагромадження нулів – це метод обчислення визначника, що спирається на властивість 6-7 і полягає у послідовному застосуванні властивості 6 з метою утворення в деякому рядку (ст.) певну кількість нулів, а потім застосовується властивість 7.
Означення :
Мінором (Мi j) i,j=1,3 визначника ∆, що відповідає елементу аi j цього визначника, називається визначник 2-го порядку, здобутий з визначника ∆ викресленням і-го рядка і j-го стовпця, на перетині яких стоїть аі j.





 а11
а12
а13
а21
а23
а11
а12
а13
а21
а23
∆= а21 а22 а23 М12= а31 а33
а31 а32 а33
Означення :
Алгебраїчним доповненням елемента аі j визначника ∆ називається число ( алгебраїчний вираз ) , що дорівнює Аi j = (-1)i+j* Mi j
