Численное решение обыкновенных дифференциальных уравнений

Министерство образования и Науки Российской Федерации

Казанский национальный исследовательский технологический университет

Кафедра химической кибернетики

Лабораторная работа №6

«Численное решение обыкновенных дифференциальных уравнений»

Выполнили студенты

Гр.2361-41,62

Филипов Руслан

Анатолий Тараев Пискунов Андрей

Проверил: Шулаев М.В.

Казань, 2017

Дано: дифференциальное уравнение 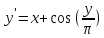с начальным условием у₀(1,7) = 5,3 на интервале [1,7; 2,7].

Задача:

1). Решить дифференциальное уравнение методом Эйлера и Рунге-Кутта в таблице Excel с h = 0,1.

2). Решить дифференциальное уравнение методом Эйлера и Рунге-Кутта в программе Visual Basic c h = 0,01, с шагом печати h_p = 0,1 по результатам решения построить точечную диаграмму.

1. Решение ДУ в таблице Excel.

2. Решение ДУ в программе Visual Basic.

Метод Эйлера.

Sub Metod_E1()

x0 = Val(InputBox("Ввод х0", "Начальное значение "))

y0 = Val(InputBox("Ввод y0", "Начальное значение"))

h = Val(InputBox("Ввод h", "Шаг интегрирования"))

hp = Val(InputBox("Ввод hp", "Шаг печати"))

b = Val(InputBox("Ввод b", "Конец интервала"))

x = x0: y = y0

i = 12

While x < b

f = x + Cos(y / 3.14)

y = y + h

x = x + h

Do While x > hp

i = i + 1

Worksheets("лаба6").Cells(i, 1).Value = x

Worksheets("лаба6").Cells(i, 2).Value = y

hp = hp + 1

Loop

Wend

End Sub

Метод Рунге-Кутта.

Sub Runge_Kytta()

h = 0.01

hp = 0.1

x0 = Val(InputBox(“Введите начальное значение x0", "Ввод х0"))

xk = Val(InputBox(“Введите начальное значение xk", "Ввод xk"))

y0 = Val(InputBox("Введите начальное значение y0", "Ввод y0"))

x = x0: y = y0

i = 20: j = 1

While x < xk

k0 = z(x, y) * h

k1 = z(x + h / 2, y + k0 / 2) * h

k2 = z(x + h / 2, y + k1 / 2) * h

k3 = z(x + h / 2, y + k2) * h

y = y + (k0 + 2 * k1 + 2 * k2 + k3) / 6

x = x + hp

Do While x > hp

i = i + 1

Worksheets("лаба6").Cells(i, j).Value = x

Worksheets("лаба6").Cells(i, j + 1).Value = y

hp = hp + 1

Loop

Wend

End Sub

Вывод: мы решили обыкновенные дифференциальные уравнения методами Эйлера и Рунге-Кутта в таблице Excel и в программе Visual Basic. Метод Рунге-Кутта оказался более точным, так как он является методом решения обыкновенных дифференциальных уравнений четвертого порядка . Этот метод с повышенной точностью и позволяет производить расчеты с более крупным шагом.