
Лаба 1-2
.docxМинобрнауки Российской Федерации
Казанский Национальный Технологический Университет
Кафедра химической кибернетики
Лабораторная работа №1-2
Выполнили:
Студенты группы 2361-62
Пискунов Андрей, Филипов Руслан
Проверил:
Шулаев М. В.
Постановка задачи:
Дана функция f(x)=3x-4ln(x)-5, равная 0, которая определена и непрерывна на интервале [a;b]. Найти x с заданной точностью Е=0,001.
1. Решить в таблице методом простых итераций.
2.Решить используя процедуру подбора параметров.
Решение:
1.Отделение корней
|
x |
f(x) |
|
1 |
-2 |
|
2 |
-1,772588722 |
|
3 |
-0,394449155 |
|
4 |
1,454822556 |
|
5 |
3,56224835 |
|
6 |
5,832962123 |
|
7 |
8,216359404 |
|
8 |
10,68223383 |
|
9 |
13,21110169 |
|
10 |
15,78965963 |
|
11 |
18,40841891 |
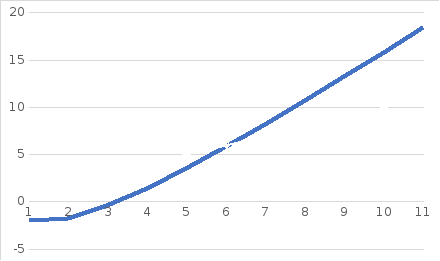
2. Решение в таблице методом простых итераций.
Для этого
представим уравнение в виде
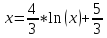
Проверим
выполнение условия сходимости:
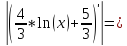

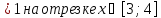
Введем в таблицу расчетную формулу метода, формулу расчета погрешности приближения и начальное приближение и определим корень с заданной точностью и число итераций:
|
x |
f(x) |
погрешность |
|
|
1 |
1,666666667 |
|
|
|
1,666666667 |
2,347767498 |
0,666666667 |
|
|
2,347767498 |
2,804619835 |
0,681100832 |
|
|
2,804619835 |
3,041690665 |
0,456852336 |
|
|
3,041690665 |
3,149884667 |
0,23707083 |
|
|
3,149884667 |
3,196487785 |
0,108194003 |
|
|
3,196487785 |
3,216070186 |
0,046603117 |
|
|
3,216070186 |
3,224213567 |
0,019582402 |
|
|
3,224213567 |
3,22758542 |
0,008143381 |
|
|
3,22758542 |
3,22897908 |
0,003371853 |
|
|
3,22897908 |
3,229554684 |
0,001393659 |
|
|
3,229554684 |
3,229792345 |
0,000575604 |
|
|
3,229792345 |
3,229890461 |
0,000237661 |
|
|
3,229890461 |
3,229930965 |
9,81158E-05 |
|

Заданная точность достигнута после 11 итераций.
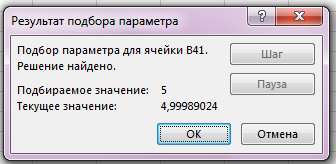
3. Решение процедурой подбора параметра.
Ввели необходимые данные:
|
x |
1 |
|
уравнение |
3 |
Совершили процедуру:
Самостоятельная работа:
Уточнение корней методами половинного деления, касательных, хорд, простой итерации в редакторе EVB.
Решение:
Function f(x)
f = x ^ 3 - 2 * x ^ 2 - 4 * x + 7
End Function
Sub Metod_polovinnogo_deleniya()
a = 3
b = 4
e = 0.001
n = 0
Do
x = (a + b) / 2
F1 = f(a)
F2 = f(b)
If F1 * F2 > 0 Then
a = x
Else
b = x
End If
n = n + 1
Loop While Abs(b - a) >= e
With Worksheets("Лист1")
.Range("E2").Value = x
.Range("F2").Value = n
.Range("G2").Value = f(x)
End With
End Sub
Sub Metod_kasatelnih()
x = 3
e = 0.0001
n = 0
Do
x1 = x - f(x) / (3 * x ^ 2 - 4 * x - 4)
c = Abs(x1 - x)
x = x1
n = n + 1
Loop While c >= e
With Worksheets("Лист1")
.Range("E3").Value = x
.Range("F3").Value = n
.Range("G3").Value = f(x)
End With
End Sub
Sub Metod_hord ()
x = 3
e = 0.001
n = 0
p = 1
Do
x1 = x - f(x) / (f(x) - f(p)) * (x - p)
c = Abs(x1 - x)
x = x1
n = n + 1
Loop While c >= e
With Worksheets("Лист1")
.Range("E4").Value = x
.Range("F4").Value = n
.Range("G4").Value = f(x)
End With
End Sub
Sub Metod_prostoi_iteracii()
e = 0.001
n = 0
x = 1
Do
x1 = (x ^ 3 - 2 * x ^ 2 + 7) / 4
c = Abs(x1 - x)
x = x1
n = n + 1
Loop While c >= e
With Worksheets("Лист1")
.Range("E5").Value = x
.Range("F5").Value = n
.Range("G5").Value = f(x)
End With
End Sub
Результаты:
|
метод |
x= |
n= |
f(x)= |
|
половин. дел. |
3,124023438 |
10 |
-0,184416625 |
|
касательных |
3,22995944 |
3 |
4,56435E-12 |
|
хорд |
3,230445221 |
171 |
0,000855796 |
|
прост. итераций |
3,229554684 |
11 |
-0,000712984 |
Вывод:
Для уравнения 3x-4ln(x)-5=0 на интервале [3;4] самым простым является метод касательных, так как используется небольшое количество итераций и найденное значение имеет наименьшую погрешность.
