6.11. Практическое занятие № 11 Анализ переходных процессов в цепях постоянного тока классическим методом

6.11.1. Вопросы для подготовки к занятиям

1. Объяснить причины возникновения переходных процессов в электрических цепях.

2. Сформулировать первый и второй законы коммутации и объяснить их физический смысл.

3. Что такое "постоянная времени" и что она характеризует?

4. В чем заключается классический метод анализа переходных процессов?

5. Как можно получить дифференциальное уравнение электрического состояния линейной электрической цепи при переходном процессе?

6. Как можно представить полное решение дифференциального уравнения с постоянными коэффициентами?

7. Каков физический смысл принужденной и свободной составляющих решения дифференциального уравнения?

8. Как определить необходимые для решения дифференциального уравнения начальные условия?

9. В чем заключается алгоритм расчета переходного процесса классическим способом?

6.11.2. Анализ переходных процессов в цепях с одним и двумя накопителями энергии (реактивными элементами)

Задача 1. Измерение активного сопротивления обмотки трансформатора производится методом амперметра-вольтметра при питании обмотки от источника постоянного напряжения через дополнительный резистор (рис. 5.19). Напряжение U = 100 В. Показания приборов при замкнутом ключе SA: I = 10 А, U = 10 В. Индуктивность обмотки трансформатора L = 100 Гн. Сопротивление вольтметра R_V = 5000 Ом. Сопротивление дополнительного резистора R_Д = 9 Ом.

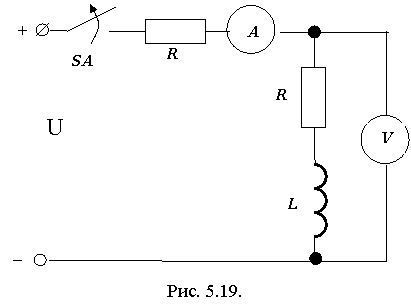
Определить:

• Величину активного сопротивления обмотки трансформатора R.

• Величину напряжения на вольтметре в момент отключения обмотки трансформатора от источника напряжения (в момент размыкания ключа SA).

• Записать закон изменения тока в обмотке трансформатора после размыкания ключа SA.

Решение. До размыкания ключа SA ток в обмотке трансформатора (при условии R_V >> R) I = U / (R_Д + R) и напряжение на обмотке U_V = I_А R, откуда R = 1 Ом. В момент отключения обмотки согласно 1-му закону коммутации ток обмотки трансформатора и вольтметра i_L(0) = i(0) = I_A = 10 A. При этом напряжение на вольтметре U_V(0) = i_V(0) R_V = 50 кВ.

Чтобы не повредить вольтметр, надо предусмотреть возможность его отключения прежде, чем будет разомкнут ключ. Поскольку при разомкнутом ключе принужденная составляющая тока равна нулю, ток в цепи определяется только свободной составляющей и уменьшается по экспоненциальному закону от I_max = I_A до нуля:

,

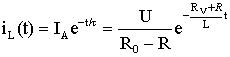что является решением дифференциального уравнения

.

Задача 2. Почему обмотку возбуждения мощной электрической машины при необходимости быстро снять возбуждение не отключают от источника постоянного напряжения, а замыкают на разрядный резистор (рис. 5.20)?

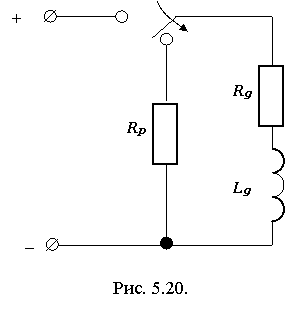
Ответ. Если просто разомкнуть цепь обмотки возбуждения, то даже при наличии электрической дуги при включении ток очень быстро уменьшается до нуля (скорость уменьшения тока di / dt очень велика). Так как обмотка возбуждения имеет большую индуктивность L_В, в ней возникает весьма значительная э.д.с. самоиндукции e_L = -L di / dt, которая может пробить изоляцию на корпус машины или между витками.

Задача 3. Определить емкость С конденсатора из условия, что через время t₁ = 20 мс после включения ключа SA (рис. 5.21) напряжение на конденсаторе при заряде его через резистор с сопротивлением R = 3,2 МОм достигает 20 В. Напряжение источника U = 200 В. До подключения конденсатор не был заряжен.

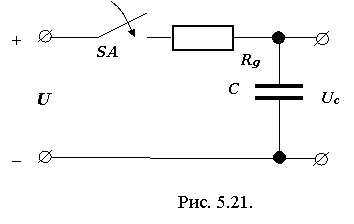
Решение. Выражение для напряжения на конденсаторе во время переходного процесса имеет вид u_C(t) = U₀(1 - e^-t1/(RC)). Из последнего выражения найдем значение емкости конденсатора С. При t₁ = 20 мс, u_C(t₁) = 20 В. Следовательно, 20 = 200 (1 - e^-t1/(RC)) , откуда e^-t1/(RC) = 180 / 200 = 0,9. Тогда -t/(RC) = ln 0,9, т.е. t₁ = 0,1; RC = 20 мс.

Таким образом, C = 20·10³ / (0,1·3,2·10⁶) = 0,062 мкФ. Выражение для тока в цепи запишем в виде

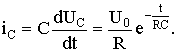
Подставляя в это выражение значения U₀ , R , C и t₁, получаем

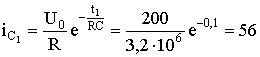мкА

Задача 4. Две параллельные ветви подключаются к источнику постоянного напряжения U (рис. 5.22). Определить емкость С конденсатора, при которой сразу после коммутации наступит установившийся режим тока i в неразветвленной части цепи, если L = 0,1 Гн, R1 = R2 = R = 20 Ом.

Ответ. Чтобы ток i в неразветвленной части цепи оставался постоянным, должно выполняться условие i = i₁ + i₂ = const. Учитывая, что i₁ = U / R e^-t/τ1; i₂ = U / R (1 - e^-t/τ2) можно записать: i = U / R (1 + e^-t/τ1 - e^-t/τ2) = U / R, т.е. τ₁ = τ₂, RC = L / R, откуда C = L / R² = 250 мкФ.

Задача 5. Конденсатор С = 10 мкФ заряжается через резистор, сопротивление которого R = 9 Ом (рис. 5.24), от источника с э.д.с. Е = 100 В и внутренним сопротивлением R₀ = 1 Ом (на схеме не показано). Через промежуток времени, равный удвоенной величине постоянной времени цепи зарядки, переключатель П переводится в положение 2. Определить энергию, израсходованную за время зарядки конденсатора.

Р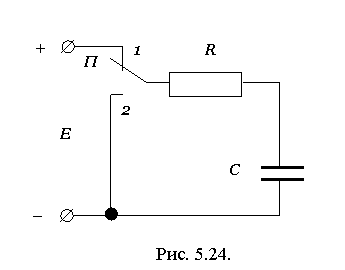ешение. Закон изменения напряжения на конденсаторе в процессе зарядки

u_C(t) = E (1 - e^-t/τ).

К моменту переключения рубильника напряжение достигает величины

Закон изменения тока в процессе зарядки конденсатора

.

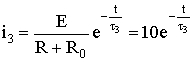Энергия, израсходованная в сопротивлении R при зарядке конденсатора:

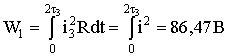
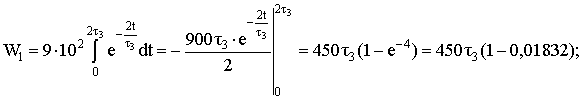
R₃ = (R + R₀) C = 10^-4 C; W₁ ≈ 450·10^-4Дж

Задача 6. Рассчитаем переходный процесс в разветвленной цепи постоянного тока (рис. 2.23). Исходные данные: Е = 120 В, L = 500 мГн, С = 1 мкФ, R = 200 Ом, u_C(0) = 50 В.

Задачу решаем классическим методом. Электрическое состояние цепи после коммутации описывается дифференциальными уравнениями для мгновенных значений на основании 1-го и 2-го законов Кирхгофа:

i = i₂ + i₃; L di₂/dt = i₃ R; E = u_C + i₃ R.

Учитывая, что i = C du_C / dt, решаем систему уравнений относительно u_C и получаем дифференциальное уравнение второго порядка:

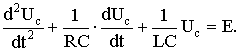
Решение дифференциального уравнения состоит из принужденной и свободной составляющих:

u_C(t) = u_Cпр(t) + u_Cсв(t).

Принужденная составляющая напряжения на емкости u_Cпр(t) = E, так как после окончания переходного процесса в цепи ток не протекает.

Для нахождения свободной составляющей напряжения на емкости u_Cсв(t) решим характеристическое уравнение

Корни уравнения

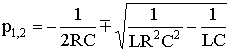
Подставляя значения, получаем

p_1,2 = (-0,25·10⁴ ± 0,206·10⁴), c^-1

Следовательно, p₁ = -440 c^-1, p₂ = 4560 c^-1. Так как корни действительные и различные, свободная составляющая напряжения на емкости

u_Cсв(t) = A₁ e^-440t + A₂ e^-4560t,

а искомое напряжение u_C(t) = 120 + A₁ e^-440t + A₂ e^-4560t.

Постоянные интегрирования A₁ и А₂ находим, исходя из начальных условий и уравнений цепи:

u_C(0_-) = u_C(0₊) = -50 В; i₂(0_-) = i₂(0₊) = 0.

Для момента коммутации можно записать:

i₁(0) = i₂(0) + i₃(0) = 0 + i₃(0) = i₃(0); E = i₃(0) R + u_C(0); i₃(0) = (E - u_C(0)) / R = 0,85 А,

так как

,

Продифференцировав выражение для u_C(t) и подставив t = 0, будем иметь систему двух алгебраических уравнений для определения постоянных интегрирования A₁ и А₂:

A₁ + A₂ = -170; - 440 A₁ - 4560 A₂ = 0,85·10⁶.

Таким образом, получаем: А₂ = -188,155, А₁ = 18,155. Мгновенное значение напряжения на емкости

u_C(t) = 120 + 18,155 e^-440t - 188,155 e^-4560t, B

Для определения тока i₁(t) используем известное соотношение

i₁(t) = C du_C / dt = -7,988·10^-3 e^-440t + 0,858 e^-4560t,

Ток i₃(t) целесообразно определить из уравнения

i₃(t) = (E - u_C(t)) / R = -0,091 e^-440t + 0,941 e^-4560t.

Следовательно,

i₂(t) = i₁(t) - i₃(t) = 0,083 e^-440t - 0,083 e^-4560t.

По полученным аналитическим выражениям мгновенных значений токов нетрудно построить временные диаграммы.

Длительность переходного процесса определяется от момента коммутации до момента времени, когда значение тока (напряжения) отличается от установившегося, например, не более чем на 5 %. Это время можно определить по аналитическим выражениям или по временным диаграммам.