12. Прямые и косвенные измерения. Погрешности.

Прямые измерения-числовые значения искомой величины получаются сравнением её с мерой(температура,длина,расстояние).

Косвенные-водятся к нахождению значения искомой величины по известной зависимости между нею и измеренными величинами.

Погрешность-количественная х-ка качества измерения.

Абсолютная погрешность(дельта х)-разность между результатом измерения и истиным значением измеряемой величины.

дельта х=х-х0.

Относит.погрешность(Е)

Е=дельта х/х0*100%

Систематич. погрешности сохраняют постоянное значение или изменяются по известному закону в ходе измерения.

Пример:уличный термометр(дельта х=3 градусаС)Чаще всего к систематич. относят приборные погрешности(инструментальные).Они обусловлены особенностью самого измерит. средства и его характеристиками(цена деления прибора).Грубые погрешности(промахи)-возникают при резких изменениях условий измерений или ошибках самого оператора.(дельта t=1 час)

Пример:37.1,37.0,39.9,36.9,37.1

Результат грубой погрешности приводит к резкому отличию данных.

Случайная погрешность-составляющая погрешности измерения, изменяющаяся случайным образом в серии повторных измерений одной и той же величины

13.Методы оценки приборной и случайной погрешностей. Коэффициент Стьюдента. Методы оценки косвенных измерений.

Способы учета приборной погр.: 1)из паспорта(часы, ход часов, приборная погр.). Класс точности прибора- выраженное в процентах отношение абс. погр к наиб знач измеряемой величины( предел измер-я), к-рое можно определить данным прибором.2) цифровые – погрешность=наим. разряду. Прибор со шкалой – линейка – если шкала не закреплена, тогда погрешность прибора=цене наим. деления шкалы. Если шкала закреплена, тогда погр.=половине цены наим деления шкалы.

нормальный закон случайных погрешностей Гаусса----погрешности измерений могут принимать непрерывный ряд значений;----при большом числе измерений погрешности одинаковой величины, но разного знака встречаются одинаково часто,----чем больше величина случайной погрешности, тем меньше вероятность ее появления. где 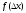- функция распределения случайных ошибок (погрешностей), характеризующая вероятность появления ошибки 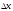, σ – средняя квадратичная ошибка. Величина σ не является случайной величиной и характеризует процесс измерений. Если условия измерений не изменяются, то σ остается постоянной величиной. Квадрат этой величины называют дисперсией измерений. Чем меньше дисперсия, тем меньше разброс отдельных значений и тем выше точность измерений.Точное значение средней квадратичной ошибки σ, как и истинное значение измеряемой величины, неизвестно. Существует так называемая статистическая оценка этого параметра, в соответствии с которой средняя квадратичная ошибка равняется средней квадратичной ошибке среднего арифметического . Величина которой определяется по формуле

, где - результат i-го измерения; - среднее арифметическое полученных значений; n– число измерений.Чем больше число измерений, тем меньше и тем больше оно приближается к σ. Если истинное значение измеряемой величины μ, ее среднее арифметическое значение, полученное в результате измерений , а случайная абсолютная погрешность 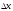, то результат измерений запишется в виде .

Интервал значений от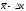 до , в который попадает истинное значение измеряемой величины μ, называется доверительным интервалом. Все это справедливо для достаточно большого числа измерений, когда близка к σ. Для отыскания доверительного интервала и доверительной вероятности при небольшом числе измерений, с которым мы имеем дело в ходе выполнения лабораторных работ, используется распределение вероятностей Стьюдента. Это распределение вероятностей случайной величины , называемой коэффициентом Стьюдента, дает значение доверительного интервала 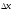в долях средней квадратичной ошибки среднего арифметического .

. Распределение вероятностей этой величины не зависит от σ², а существенно зависит от числа опытов n. С увеличением числа опытов nраспределение Стьюдента стремится к распределению Гаусса.Для нахождения случайной погрешности косвенного измерения вначале рассчитываются средние квадратичные ошибки среднего арифметического отдельных измерений. Затем находится средняя квадратичная ошибка величины y. Задание доверительной вероятности α, нахождение коэффициента Стьюдента , определение случайной и суммарной ошибок осуществляются так же, как и в случае прямых измерений. Аналогичным образом представляется результат всех расчетов в виде, с α=… Е=…%.