
1 Постановка задачи
Постановка задачи является первым этапом выполнения курсовой работы, на котором необходимо проанализировать задание и определить перечень вопросов, которые будут решаться в данной работе. Основное назначение этого этапа – создание списка функциональных требований к программе, то есть определение того, что, собственно, будет выполнять разрабатываемая программа, определить перечень взаимно независимых фрагментов или функций (модулей), не рассматривая конкретную реализацию этих функций.
Цель
курсовой работы-это разработка программы,
которая будет производить решение
нелинейного уравнения
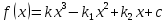 ,
методом деления отрезка пополам. Также
программа должна построить график и
вывести результаты расчётов в таблицу.
,
методом деления отрезка пополам. Также
программа должна построить график и
вывести результаты расчётов в таблицу.
2 Математическая модель
Метод деления отрезка пополам - простейший численный метод для решения нелинейных уравнений вида f(x)=0. Предполагается только непрерывность функции f(x). Поиск основывается на теореме о промежуточных значениях.
Алгоритм
основан на следующем следствии из
теоремы Больцано-Коши: Пусть непрерывная
функция
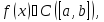 тогда,
если
тогда,
если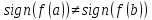 ,
то
,
то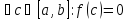 .
.
Таким образом, если мы ищем ноль, то на концах отрезка функция должна быть противоположных знаков. Разделим отрезок пополам и возьмём ту из половинок, на концах которой функция по-прежнему принимает значения противоположных знаков. Если значение функции в серединной точке оказалось искомым нулём, то процесс завершается.
Точность вычислений задается двумя способами:
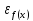 по
оси у, что ближе к условию
по
оси у, что ближе к условию
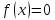 .
.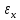 по
оси x,
что может показаться удобным в некоторых
случаях.
по
оси x,
что может показаться удобным в некоторых
случаях.
Процедуру следует продолжать до достижения заданной точности. Для поиска произвольного значения достаточно вычесть из значения функции искомое значение и искать ноль получившейся функции.
Например: Найдем середину отрезка [a, b]: c=(a+b)/2. Корень остался на одной из частей: [a, c] или [c, b]. Если f(a) * f(с)<0, то корень попал на отрезок [a, c], тогда деление отрезка можно повторить, приняв в качестве нового правого конца точку c, т.е. b=c. В противном случае корень попал на половину [c, b], и необходимо изменить значение левого конца отрезка: a=c. Поскольку корень всегда заключен внутри отрезка, итерационный процесс можно останавливать, если длина отрезка станет меньше заданной точности: |b – a|< ε.
Найдем
первый корень уравнения f(x)=x3-6x2+3x+11=0
с точностью ![]()
Вычисление оформим в виде таблицы.
|
a |
b |
Середина |
f(a) |
f(середина) |
|
-2 |
-1 |
-1,5 |
-27 |
-10,375 |
|
-1,5 |
-1 |
-1,25 |
-10,375 |
-4,07813 |
|
-1,25 |
-1 |
-1,25 |
-4,07813 |
-1,39258 |
|
-1,125 |
-1 |
-1,0625 |
-1,39258 |
-0,1604 |
|
-1,0625 |
-1 |
-1,03125 |
-0,1604 |
0,42868 |
3 Разработка алгоритма решения задачи(блок-схема)
Начало
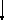
k, k1, k2, t, a, b, c, fa, fc, c1
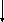

c1 = (a + b)/2
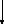
fa=k*a3-k1*a2+k2*a+c
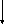
fc= k*c13-k1*c12+k2*c1+c
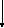
Вывод в таблицу:
a,b,c1,fa,fc
fc==0
Нет
fa*fc<0
Да
Нет
b=c1
a=c1

Конец


