7. Линейные однородные системы с постоянными коэффициентами

Линейная однородная система с постоянными коэффициентами имеет вид

(22)

где постоянные действительные числа. В матричном виде система записывается так:

(23)

где Будем рассуждать так же, как при решении однородных уравнений с постоянными коэффициентами, т.е. попробуем найти решения вида(постоянный вектор,постоянное число), а затем из этих решений составить общее решение системы. Продифференцируем функциюПодставим это выражение в уравнение (23):Сократив набудем иметь:Это равенство означает, чтособственный вектор матрицы аеёсобственное значение. Как известно из линейной алгебры, собственные значения матрицы могут быть найдены из характеристического уравнения

(24)

где единичная-матрица, а собственные векторы находятся мз системы линейных уравнений

(25)

Уравнение (24) и систему (25) можно записать в развёрнутом виде:

(26)

(27)

Предположим, что имеет место “самый хороший” случай: корни характеристического уравнения действительны и различны. В этом случае, решив для каждого систему уравнений (27), мы получимлинейно независимых собственных векторовЭти векторы определяютлинейно независимых вектор-функцийявляющихся решениями системы (22), а значит, образующими фундаментальную систему решений этой системы. Таким образом, общее решение системы (22) имеет вид

(28)

где произвольные постоянные. Рассмотрим пример.

Пример 1. Система

Найдём все решения этой системы. Вначале запишем эту систему в матричном виде: Составим характеристическое уравнение:Имеем:откудаНайдём теперь собственные векторы. Длянадо решить системуа длярешить системуРешением первой системы будет вектора второй системы – векторИз формулы (28) получаем формулу общего решения нашей системы:

где произвольные постоянные. От векторной формы общего решения можно перейти к обычной форме:

Предположим, что характеристическое уравнение имеет кратный корень В этом случае, как и в случае простых корней, мы находим собственные векторы из системы (27), и если окажется, что существуетлинейно независимых собственных векторов, то общее решение системы также запишется в виде (28). Если же собственных векторов “не хватает” до базиса пространствато можно искать решения системы в видеи т.д. Для матриц больших размеров такой метод является неприемлемым, и фундаментальную систему решений системы (23) находят, приводя матрицукжордановой нормальной форме. Мы этот метод рассматривать не будем, а ограничимся матрицами небольших размеров.

Пример 2. Система

Найдём все решения этой системы. Характеристическое уравнение

имеет корни Для собственных векторов смы имеем системуиз которой находим два линейно независимых собственных вектора:иСобственные векторы, соответствующиенаходятся из системыПолучим: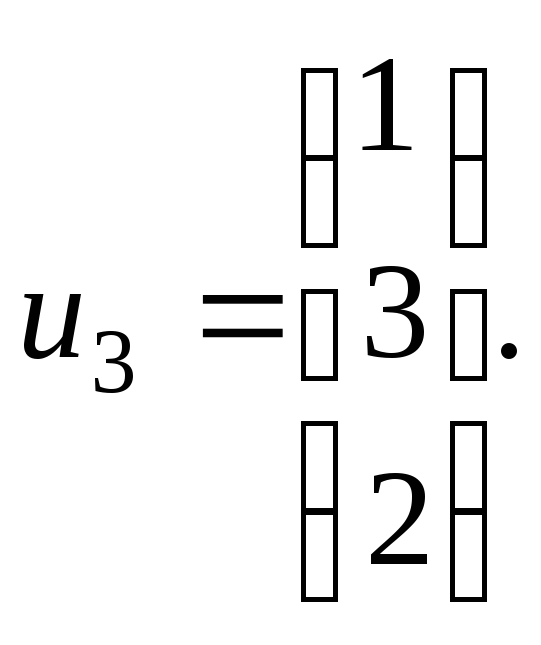Так как векторылинейно независимы, то мы можем с их помощью записать общее решение системы:

Пример 3. Система

Характеристическое уравнение имеет корниДля собственных векторов смы имеем системуиз которой находим вектор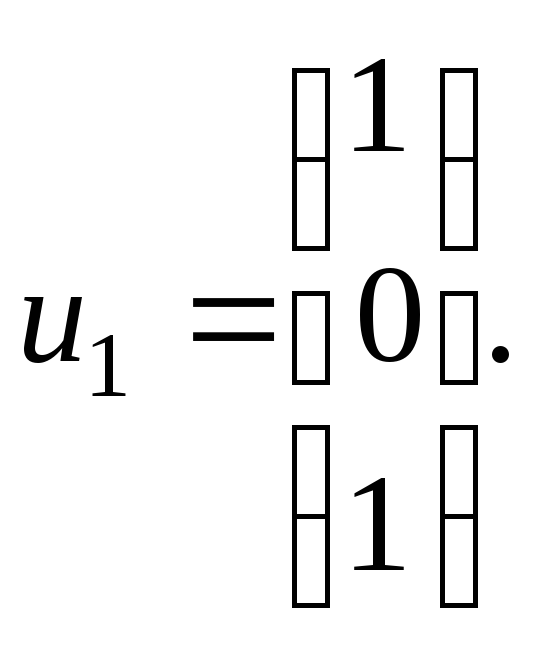Дляимеем системурешения которой имеют видгдеСобственные векторыне составляют базиса пространстваПоэтому будем искать решения системы дифференциальных уравнений, имеющие видгдепостоянные векторы. В нашем примерено мы проделаем выкладки для произвольногоИмеем:Подставим в систему дифференциальных уравнений:Отсюда следует, что

Таким образом, собственный вектор. Векторудовлетворяющий уравнениюв линейной алгебре называюткорневым вектором. В нашем примере а для векторамы имеем системут.е.Этой системе удовлетворяет, например, векторЗначит,ещё одно решение системы дифференциальных уравнений. Итак, теперь найдены три линейно независимых решения системы дифференциальных уравнений, поэтому мы можем написать её общее решение:

Наконец, выясним, как найти решения системы (23), соответствующие комплексным собственным значениям матрицы А. Пусть комплексный корень характеристического уравнения, асоответствующий ему собственный вектор. Имеем:Тогдакомплексное решение системы (23). Пустьгдедействительные вектор-функции. Так кактои мы получаем:иТаким образом, вектор-функцииитоже решения системы.

Проиллюстрируем эти рассуждения примером.

Пример 4. Система

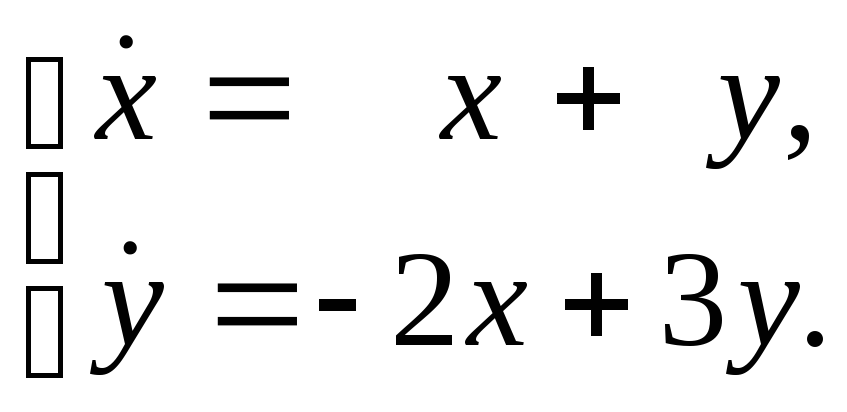
Чтобы решить систему, вначале составим характеристическое уравнение: Отсюдаа значит,Собственный вектор, соответствующий собственному значениюнайдём из системыт.е.Решив систему, получим:Следовательно,комплексное решение системы. Отделим в вектор-функциидействительную часть от мнимой:

Отсюда получаем: и мы можем выписать общее решение системы:

Подведём итог рассуждениям этого параграфа, сформулировав теорему. Недоказанным в этой теореме останется лишь утверждение (г) и метод нахождения решений в случае отсутствия базиса из собственных векторов. Эти недостающие детали можно найти в более подробных учебниках по дифференциальным уравнениям.

Теорема. Решения системы дифференциальных уравнений с постоянными коэффициентами могут быть получены следующим образом:

(а) если корни характеристического уравнениядействительны и различны, то общее решение системы имеет вид

где собственные векторы, соответствующие собственным значениямапроизвольные постоянные;

(б) если корни характеристического уравнения действительные, не обязательно различные, но существует базиспространствасостоящий из собственных векторов (соответствующих числам), то также

(в) если комплексный корень характеристического уравнения исоответствующий собственный вектор, то вектор-функциииявляются решениями системы дифференциальных уравнений;

(г) если кратный корень характеристического уравнения, то ему соответствует решение системы, имеющее вида есликомплексный корень, то следует взятьи