3. Дифференцирование векторов, матриц, определителей. Комплекснозначные функции действительного аргумента

Дифференцирование векторов и матриц осуществляется по обычным правилам:

если вектор-функция, то

если матрица, состоящая из функций отто

Операция дифференцирования является линейной в том смысле, что для вектор-функцийи константдля матрици констант

Аналогичным образом осуществляется интегрирование вектор-функций и матриц. А именно,

Дифференцирование произведений векторов и матриц (скалярное, векторное и смешанное произведение векторов, произведение матриц, произведение вектора на скаляр и т.д.) сохраняет многие, но не все свойства, присущие дифференцированию произведения обычных функций. Так, например, если векторы изкоординаты которых зависят от переменнойиих скалярное произведение, тоДля векторного произведения такжено в общем случаеАналогично этому для произведения матрицИнтересно отметить, чтоа правильная формула выглядит так:Докажем в качестве примера формулу дифференцирования скалярного произведения векторов. ПустьТогда

Дифференцирование определителя может быть выполнено на основании следующей теоремы.

Теорема.

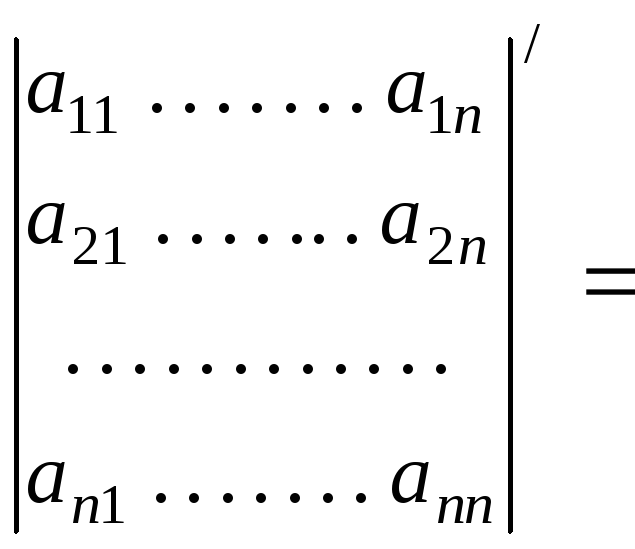
Доказательство. Определитель матрицызаписывается формулой

где суммирование ведётся по всем подстановкам аобозначает количество инверсий в подстановкеПоэтому

откуда следует требуемое равенство.

Комплекснозначная функция действительного аргументаопределяется как функция отзначения которой – комплексные числа. Она может быть представлена в видегдеаобычные действительные функции. Функциюможно рассматривать как вектор-функциюпоэтому для производной имеет место равенство

Проверим, что для комплексных функций действительного аргумента справедливо равенство

(9)

Действительно, пусть Тогда

поэтому

С другой стороны,

Видно, что эти выражения совпадают.

Для дифференциальных уравнений с постоянными коэффициентами имеет важное значение функция гдеС. Воспользуемся для преобразования этого выражения формулой Эйлера: ЕслигдеR, то Докажем, что для комплексного числаимеет место обычная формулаДействительно,

Примеры решения задач

1. Доказать формулу где иматрицы размеровисоответственно.

Решение. -й элемент произвольной матрицыХ будем обозначать символом ПустьТогдаОтсюда

2. Вывести формулу дифференцирования смешанного произведения векторов.

Решение.

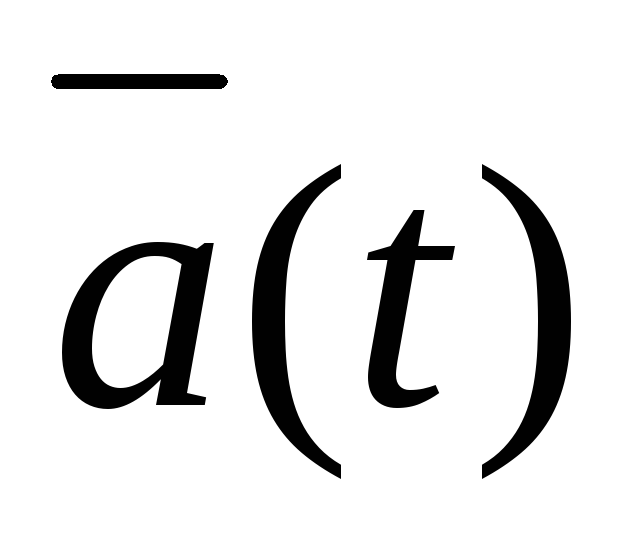3. Доказать, что если вектор имеет постоянную длину, то векторыиперпендикулярны друг другу.

Решение. Так как то скалярное произведениеОтсюда получаем:Отсюда получаем:т.е.Это означает, что

4. Пусть действительная функция, акомплекснозначная. Доказать, что

Доказательство. Пусть гдедействительные функции. Тогда

Задачи для самостоятельного решения

1. Пусть квадратная-матрица. Выразить черезипроизводные: а)б)(в случае, когдав)гдеобозначает транспонирование.

2. Доказать, что гдеС.

3. Доказать, что для комплекснозначных функций действительного аргумента справедлива формула

4.Определитель Вронского

Пусть какие-либо (не обязательно линейно независимые) решения однородной системыгде-матрица из непрерывных на отрезкефункций. Вектор-функциизапишем в виде столбцов:Определителем Вронского (или вронскианом) однородной системы дифференциальных уравнений называется определитель

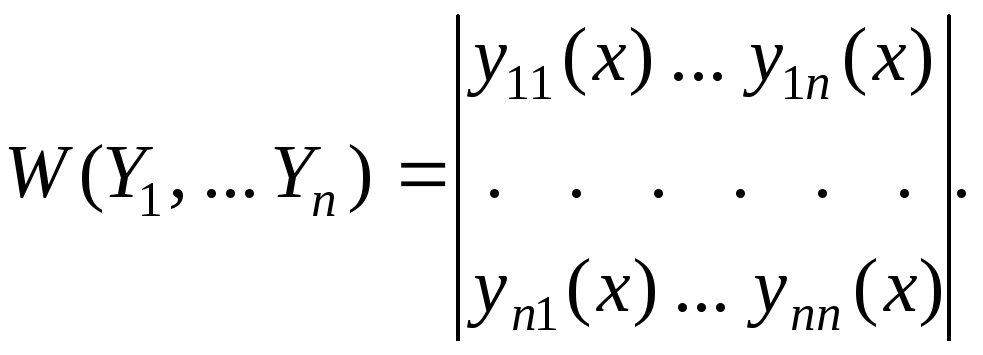
Этот определитель является функцией от дифференцируемой на интервале

Пусть дано линейное однородное дифференциальное уравнение п-го порядка

где непрерывные на отрезкефункции, и пустькакие-либо (не обязательно линейно независимые) решения этого уравнения.Определителем Вронского (или вронскианом) линейного однородного уравнения называется определитель

Выведем формулу дифференцирования определителя Вронского. Пусть решения системыисоответствующий им определитель Вронского. Тогда

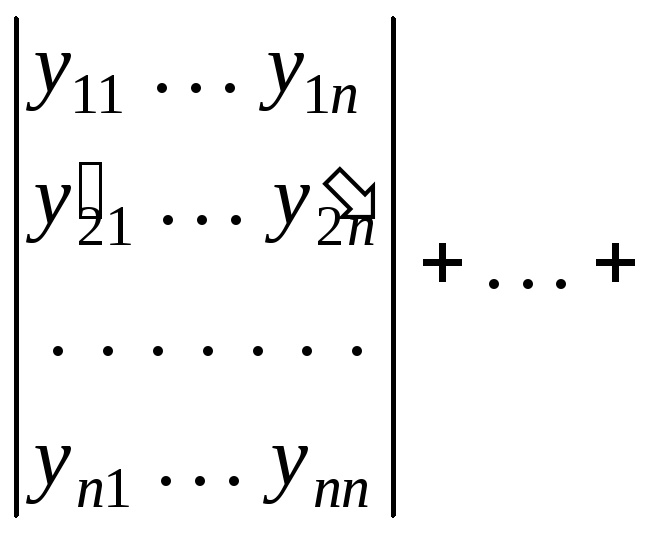
т.е. гдеТак какрешение системы, топоэтому-я строка матрицы определителяравна

Следовательно,

(в этой сумме все определители, кроме -го, равны 0, так как содержат одинаковые строки). Итак,Следовательно,Сумма диагональных элементов матрицыназываетсяследом и обозначается Таким образом,Отсюда следует, чтоРешая это дифференциальное уравнение, получим:

Константу можно найти, взявМы получим:Отсюда следуетформула Лиувилля:

Так как никогда не обращается в 0, то мы получаем следующее свойство вронскиана:если определитель Вронского равен нулю в какой-нибудь точке, то он тождественно равен нулю:

Формулу Лиувилля для однородного уравнения нетрудно получить, сведя уравнение к системе. В этом случае матрица системы имеет вид

Её след поэтому

Так же, как и в случае систем, определитель Вронского однородного уравнения либо не обращается в нуль ни в одной точке, либо тождественно равен нулю.

С помощью определителя Вронского можно определять, является ли данная система решений фундаментальной системой решений.

Теорема. Система решений однородной системыявляется её фундаментальной системой решений в том и только том случае, если

Доказательство. Если не является фундаментальной системой решений, то функциилинейно зависимы, поэтомудля некоторых константR, не все из которых равны нулю. Следовательно, столбцы определителя Вронского линейно зависимы, а значит,

Наоборот, пусть Возьмём какое-нибудьТогда мы получим линейно зависимые векторыСледовательно,для некоторых константсреди которых есть ненулевые. Функцияявляется решением системы и удовлетворяет начальному условиюВвиду единственности решенияа это означает линейную зависимость функцийСледовательно, эти функции не образуют фундаментальную систему решений.

Аналогичный результат имеет место для однородных уравнений п-го порядка:

Теорема. Функции являющиеся решением уравненияобразуют фундаментальную систему решений этого уравнения в том и только том случае, если