
МАТЕМАТИКА
.pdf
Документ СМК |
Ф 11/13-1.05-2013 |
|
|
|
|
Тестовое задание |
Редакция 3 |
|
Дата введения 01.09.2013 |
|
|
|
|
A) b Lim( f (x) kx)
x
181.Совокупность всех первообразных функции называется: A) Неопределенным интегралом от функции f (x)
182.Укажите свойство неопределенного интеграла:
A) df (x) f (x) C
183.Укажите свойство неопределенного интеграла:
A)f (x)dx / f (x)
243. Укажите формулу интегрирования заменой переменной в неопределенном интеграле:
A) f (x)dx f (t) / (t)dt
185. Найдите интеграл |
5 |
|
|
|
dx : |
|||||
(x |
3) |
3 |
||||||||
|
|
|
|
|
|
|
|
|||
A) |
|
|
5 |
C |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
2(x 3)2 |
|
|
|
|
|
|||||
186.Найдите интеграл |
ln2 x |
dx : |
||||||||
x |
||||||||||
A) |
ln3 x |
C |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
||
187. Найдите интеграл
A) cos4 x C 4
188.Найдите интеграл
A)arcsin 4x C
189.Найдите интеграл
A)12 arctg 2x C
cos3 xsin xdx :
|
dx |
: |
16 x2 |
x2dx 4 :
Документ СМК |
Ф 11/13-1.05-2013 |
|
|
|
|
Тестовое задание |
Редакция 3 |
|
Дата введения 01.09.2013 |
|
|
|
|
190.Какой метод применяется при нахождении интеграла arcsin xdx :
A)Интегрирование по частям
191.Найдите интеграл sin5xdx:
A)15 cos5x C
192.Найдите интеграл x cos xdx:
A)xsinx+cosx+C
193.Найдите интеграл ln xdx:
A)xln x x C
194.Найдите интеграл xdx1 :
A)ln x 1 C
195.Найдите интеграл e3x 5dx :
А) 13 e3x 5 C
196. Укажите формулу интегрирования по частям в неопределенном интеграле: A) Sudv = u*v-Svdu
197. Найдите интеграл
A) |
x2 |
2cos |
x |
C |
|
|
|||
|
2 |
2 |
|
|
198. Найдите интеграл
А) x ln x C
199. Найдите интеграл
|
|
|
|
x |
|
x |
sin |
|
dx : |
||
|
|||||
|
|
|
|
2 |
|
|
x 1 |
|
|
||
|
|
|
dx : |
|
|
x |
|
|
|
||
sin2 xdx :

|
Документ СМК |
Ф 11/13-1.05-2013 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Тестовое задание |
Редакция 3 |
|
||||||||
|
Дата введения 01.09.2013 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
A) |
|
x |
|
1 sin 2x C |
|
|
|||||
2 |
|
|
|||||||||
|
|
|
4 |
|
|
|
|
|
|||
|
200. Найдите интеграл cos |
x |
dx : |
|
|
||||||
|
|
|
|
||||||||
|
|
|
|
|
4 |
|
|
|
|||
|
А) |
|
4sin |
x |
C |
|
|
||||
|
|
|
|
|
|||||||
|
|
|
|
|
4 |
|
|
|
|
|
|
|
201. Найдите интеграл sin 3xsin xdx : |
|
|
||||||||
А) |
|
1 sin 2x 1 sin 4x C |
|
|
|||||||
|
|
4 |
|
8 |
|
|
|
|
|||
|
202. Найдите интеграл sin 2x cos5xdx : |
|
|
||||||||
А) |
1 |
cos7x 1 cos3x C |
|
|
|||||||
|
|
14 |
6 |
|
|
|
|
||||
203.Найдите интеграл sin 2 xdx :
А) 12 x 14 sin 2x C
204.Найдите интеграл cos2 xdx :
А) 12 x 14 sin 2x C
205.С помощью универсальной подстановки t tg 2x найдите интеграл sindxx :
А) ln tg 2x C
206. Найдите интеграл sin 3 xdx :
А) 1 cos3 x cos x C |
|
|
|
|
|
|||||||||
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
207. Найдите интеграл |
5dx |
|
|
|
: |
|||||||||
x |
2 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||
А) 5ln |
|
|
x 2 |
|
C |
3dx |
|
|
|
|
||||
|
|
|
|
|
|
|
||||||||
208. Найдите интеграл |
|
|
: |
|||||||||||
2x 5 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||
А) 3 ln |
|
2x 5 |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
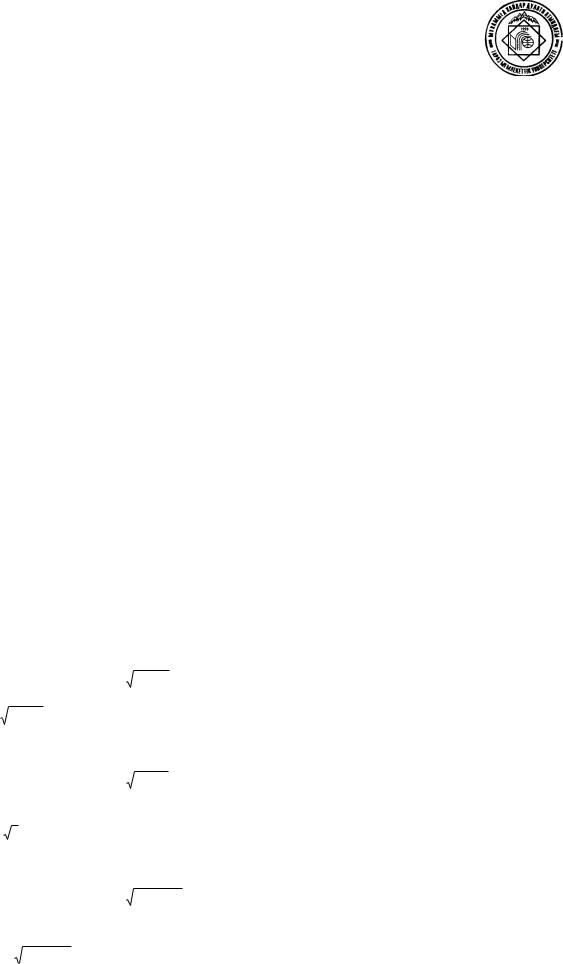
|
Документ СМК |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ф 11/13-1.05-2013 |
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Тестовое задание |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Редакция 3 |
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Дата введения 01.09.2013 |
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
209. Найдите интеграл |
dx |
|
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
(x 2) |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
А) |
|
|
|
|
|
|
1 |
|
|
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
2(x 2)2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
210. Найдите интеграл |
|
dx |
|
|
|
|
|
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
(3x 4) |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
А) |
|
|
|
|
|
1 |
|
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
3(3x 4) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
211. Укажите простейшую дробь 3-го типа |
|
|
5x 8 |
dx , |
|
3x 2 |
|
dx , |
|
dx |
|
, |
||||||||||||||||||||||||||||||||||||||
|
x |
2 |
2x 5 |
x |
2 |
4x 1 |
(3x 7) |
3 |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
x 4 |
|
|
|
|
|
dx : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
2x2 3x 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
А) |
|
|
|
|
|
|
5x |
8 |
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
x |
2 |
2x 5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
212. Найдите интеграл |
|
|
|
dx |
|
|
|
|
|
|
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
(x |
2)(x |
1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
А) ln |x 1| ln |x 2| +C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
213. Найдите интеграл |
|
|
|
dx |
|
|
|
|
|
|
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
(x |
2)(3 |
x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
А) ln |
|
x 2 |
|
ln |
|
3 x |
|
C |
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
214. Найдите интеграл |
|
|
|
|
|
|
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
x |
2 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
А) ln |
x x2 9 |
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
215. Найдите интеграл |
dx |
|
|
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
3 x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
А) |
arcsin |
x |
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
216. Найдите интеграл |
|
|
|
|
|
dx |
|
|
|
|
|
|
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4x2 49 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
А) |
1 ln x |
|
4x2 49 |
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||

Документ СМК |
Ф 11/13-1.05-2013 |
|
|
|
|
Тестовое задание |
Редакция 3 |
|
Дата введения 01.09.2013 |
|
|
|
|
217. Укажите формулу тригонометрии , которая используется при интегрировании произведений синусов и косинусов:
А) sin sin 12 cos( α−β)+ 12 cos( )
218. Укажите формулы тригонометрии , которые используются при вычислении интегралаsin m x cosn xdx , где m и n-четные неотрицательные числа:
А) |
sin 2 x |
1 cos2x |
; cos2 |
x |
1 cos2x |
|
|
2 |
|
|
2 |
219. Рациональная дробь P x R x где R x ,Q x многочлены с действительными
Q x
коэффициентами называется правильной, если:
A) . Степень числителя больше степени знаменателя
|
|
2x 1 |
|
|
220. |
Подынтегральная функция |
|
dxявляется..: |
|
x 3 x 4 |
|
|||
A) Рациональной функцией |
|
|||
221. |
Укажите формулу Ньютона-Лейбница, если F x первообразная функции |
f x : |
||
b
f (x)dx F (x) ba F (b) F (a)
A)a
6 |
dx |
|
|
222. Вычислите интеграл |
: |
||
|
|||
1 |
x 3 |
||
А) 2 |
|
|
|
4
223. Вычислите интеграл sin 4xdx :
0
А) 12
2
224. Вычислите интеграл x2 2x 3 dx :
1
А) 73 225. Какое отношение верно:
Документ СМК |
|
|
|
Ф 11/13-1.05-2013 |
|
||
|
|
|
|
|
|
|
|
Тестовое задание |
|
|
|
Редакция 3 |
|
||
|
|
|
Дата введения 01.09.2013 |
|
|||
|
|
|
|
|
|
|
|
|
b |
a |
|
|
|
|
|
A) |
f (x)dx f (x)dx |
|
|
|
|
||
a |
b |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
8 |
dx |
|
|
|
226. Вычислите интеграл 0 |
: |
|
|
||||
cos2 2x |
|
|
|||||
A) |
2 |
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
1
227. Вычислите интеграл xe x dx :
0
А) 1
228. Укажите формулу интегрирования по частям в определенном интеграле :
bb
A)udv uv ba vdu
aa
229. Какой из интегралов представляет определенный интеграл
|
|
2 |
0 |
dx |
|
|
xsin xdx; |
exdx; |
x2dx; |
|
|
: |
|
1 x |
2 |
|||||
|
0 |
1 |
|
|
|
|
2 |
|
|
|
|
|
|
А) x2dx |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
230. Укажите формулу нахождения площади плоской фигуры:
b
S f x dx
А) a
231.Площадь фигуры, ограниченной линиями y 0, x 2, y x2 равна:
A)S 83
232.Вычислите площадь фигуры, ограниченной линиями y x2 1, y 0, x 0, x 2:
A)S 143
233. Площадь фигуры, ограниченной линиями y 0, x 1, x 4, |
y |
1 |
, равна: |
|
x |
||||
|
|
|

Документ СМК |
Ф 11/13-1.05-2013 |
|
|
|
|
Тестовое задание |
Редакция 3 |
|
Дата введения 01.09.2013 |
|
|
|
|
A)S=2
234.Вычислите площадь фигуры, ограниченной линиями y ex , y 0, x 0, x 1: A) S=e-1
235.Вычислите площадь фигуры, ограниченной линиями y sin x, y 0, x 0, x :
A)S=2
236.Вычислите площадь фигуры, ограниченной линиями y 1x , y 0, x 2, x 1 :
A)S ln 2
237.Вычислите площадь фигуры, ограниченной линиями y x4 , y 0, x 1, x 2 :
A)S 6 15
238.Вычислите площадь фигуры, ограниченной линиями y x2 , y 2x :
A)S 1 13
239.Вычислите площадь фигуры, ограниченной линиями y2 2x , y 0, x 2 :
A)S 2 23
240.Найти объем тела, образованного вращением вокруг оси Oy фигуры, ограниченной
параболой y x2 , осью Oy и прямыми y 0, y 1.
A) Vy
2
241. Объем тела, образованного вращением вокруг оси Ox фигуры, ограниченной кривой
y f (x) , осью Ox и прямыми x a, |
x b вычисляется по формуле: |
b
A) Vx f 2 (x)dx
a
242. Найти частные производные функции z ex2 y2 :
/ |
2xe |
x2 y2 |
/ |
2ye |
x2 |
y2 |
A) zx |
, |
zy |
|
|

Документ СМК |
Ф 11/13-1.05-2013 |
|
|
|
|
Тестовое задание |
Редакция 3 |
|
Дата введения 01.09.2013 |
|
|
|
|
243. |
Частная производная первого порядка по переменной y функции |
|
|
|||||||
u x2 2x y2 2y 2 равна: |
|
|
|
|
|
|
||||
A) 2y+2 |
|
|
|
|
|
|
|
|
|
|
244. |
|
|
|
|
|
|
|
u |
|
|
Найдите частную производную первого порядка |
функции u 2y |
|||||||||
|
|
|
|
|
|
|
|
x |
|
|
A) -2x |
|
|
|
|
|
|
|
|
|
|
245. |
y |
z |
|
ln x |
|
e |
y : |
|
|
|
Найти z / , функции |
|
|
|
|
|
|
|
|
||
A) |
|
|
|
|
|
|
|
|
|
|
246. |
Найти для функции z 2x3 |
6y2 15x2 y 5 значение выражения |
z |
|
||||||
|
|
|
|
|
|
|
|
|
x |
|
A 1, 1 :
x2 y2 :
z в точке
y
A)9
247.По формуле dz fx dx fy dy вычисляется:
A) полный дифференциал функции z f (x, y )
248. Найти |
2u |
для функции u 4x3 3x2 y 3xy2 y3 : |
|
x y |
|||
|
|
A)6x+6y
249.Найдите zxy// в точке M 1,0 , если z x2 y xsin y :
A)3
250.Дана функция z xy . Найти производную zxy// :
A)
251.Дана функция z x3 y3 3bxy, найти производные zxx// , zyy// : A) 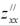 =6x;
=6x; 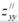 =6y
=6y

Документ СМК |
Ф 11/13-1.05-2013 |
|
|
|
|
Тестовое задание |
Редакция 3 |
|
Дата введения 01.09.2013 |
|
|
|
|
252.Найти zxy// , если z y ln x : A) 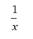
253.Найти полный дифференциал функции u xyz:
A)du=yzdx+xzdy+xydz
254.Дана f n(xy z) . Найти df (1,2,0) :
A)dx+0.5dy+0.5dz
255.Найти полный дифференциал функции f x3 xy y2 :
A)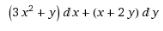
256.Найти полный дифференциал функции f 4cos xy
A) (-4ysinyx)dx+(-4xsinxy)dy
257. Найти стационарную точку Р(х0 , у0 ) функции f x2 2xy 4x 8y :
A)P(-4;6)
258.Найти стационарную точку Р(х0 , у0 ) функции f (x 1)2 2y2 :
A) P(1;0)
259. Найти стационарную точку Р(х0 , у0 ) функции f 1 6x x2 xy y2 :
A)(4;-2)
260.Точка Р(х0 , у0 ) называется стационарной, если:
|
|
f |
x0 , y0 |
0 |
|
|
|
или |
|||
A) |
|
|
|
|
|
|
x |
|
0 |
|
|
|
|
f x0 , y0 |
|
||
|
|
|
y |
|
|
|
|
|
|
|
|
261. Найти стационарные точки функции f 2х2 xу 3у2 2х 11у 1: A) (1;2)

Документ СМК |
Ф 11/13-1.05-2013 |
|
|
|
|
Тестовое задание |
Редакция 3 |
|
Дата введения 01.09.2013 |
|
|
|
|
262.Определить порядок уравнения ( y )2 y 4y x :
A)3 порядок
263. Укажите общий вид обыкновенного дифференциального уравнения первого порядка:
A) F(x, y, y')=0 , (где y = y ( x ))
264.Определить порядок уравнения y y 2 yx 5 0 :
A)2 порядок
265.Найти общее решение дифференциального уравнения y x2 :
A)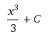
|
|
|
|
y 2 |
|
|
y |
|
|
|
|
266. |
Определить вид уравнения y |
2 x 2 |
5 x : |
|
|
|
|||||
|
|
|
|
||||||||
A) однородное уравнение |
|
|
|
|
|
|
|
|
|
|
|
267. |
Решить уравнение y sin 2x : |
|
|
|
|
|
|
|
|
|
|
A) |
|
|
|
|
|
|
|
|
|
|
|
268. |
Найдите частное решение уравнения |
dy |
2xy, |
y 0 1 |
: |
||||||
|
|
|
|
|
|
dx |
|
|
|
|
|
A) |
|
|
|
|
|
|
|
|
|
|
|
269. |
Найти частное решение уравнения dy x, |
y 0 0 : |
|
||||||||
|
|
|
|
dx |
|
|
|
|
|
||
A)
270. Определить вид дифференциального уравнения y xy e x :
A) уравнение в полных дифференциалах
271. Какое из следующих уравнений является дифференциальным уравнением с разделяющимися переменными:
A)f1(y)*g1(x)dy=f2(y)*g2(x)dx
272.Решите уравнение xy/ y 0:
