
МАТЕМАТИКА
.pdf
Документ СМК |
Ф 11/13-1.05-2013 |
|
|
|
|
Тестовое задание |
Редакция 3 |
|
Дата введения 01.09.2013 |
|
|
|
|
ТАРАЗСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИМЕНИ М.Х. ДУЛАТИ
Кафедра «Математика»
ТЕСТОВОЕ ЗАДАНИЕ 944 (с ответом)
По дисциплине «Математика (4 кредита) ГИДРО»
Для студентов 1-курса специальности 5В080500 - Водные ресурсы и водопользование 5В081000 - Мелиорация, рекультивация и охрана земель
ТЕСТОВОЕ ЗАДАНИЕ
1. Сложение двух матриц определено, если..
А) числа строк и столбцов обеих матриц соответственно равны
2. Величина определителя равна нулю, если:
А) соответствующие элементы двух строк (столбцов) пропорциональны
3. Величина определителя не изменится, если:
А) общий множитель элементов какой-либо строки (столбца) вынести за знак определителя
4.Квадратная матрица называется диагональной, если….. A) все элементы вне главной диагонали равны нулю
5.Прямоугольная матрица A размеров m nназывается квадратной, если …
A) m n
6.При умножении матрицы на число умножаются..
A) все элементы матрицы
7. Умножение двух матриц определено только тогда, когда:
А) число столбцов первой матрицы равно числу строк второй матрицы
8.Алгебраическое дополнение Àij элемента aij и минор Mij cвязаны соотношением:
А) Àij 1 i j Mij
9.Определитель квадратной матрицы второго порядка вычисляется по формуле:
А) |
|
à11 |
à12 |
|
a a a a |
21 |
||
|
|
|||||||
|
|
à21 |
à22 |
|
11 |
22 |
12 |
|
|
|
|
|
|
|
|
||

Документ СМК |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ф 11/13-1.05-2013 |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тестовое задание |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Редакция 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Дата введения 01.09.2013 |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
0 |
4 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
10. |
Найти минор элемента a11 определителя |
1 |
2 |
0 |
|
|
|
|
|
: |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
4 |
|
5 3 |
|
|
|
|
|
|
|
|
|
|||||||
A) 6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11. |
Решить уравнение |
|
x |
x 1 |
|
0 : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
4 |
x 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A) x 1, x 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
4 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
||||
12. |
Вычислить определитель квадратной матрицы третьего порядка |
0 |
2 |
3 |
|
: |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
1 |
|
|
|
|
А) |
5 (если -3 справа , то 25) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|||
13. |
Вычислить определитель квадратной матрицы третьего порядка |
0 |
2 |
5 |
|
: |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
3 |
|
|
|
|
A) 18 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Найти минор элемента a23 определителя |
|
|
1 |
2 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
14. |
|
|
4 |
5 |
6 |
|
: |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
8 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A) 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Найти A32 |
элемента a32 |
|
|
|
2 |
5 |
3 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
15. |
определителя |
|
0 |
1 |
4 |
|
: |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
3 |
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
||||
A) 8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
16. |
|
0 |
3 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пусть A |
. Вычислить определитель матрицы A : |
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
2 |
2 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
A) -21

Документ СМК |
|
|
|
|
|
Ф 11/13-1.05-2013 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||
Тестовое задание |
|
|
|
|
|
Редакция 3 |
|
|
|
|||
|
|
|
|
|
Дата введения 01.09.2013 |
|
||||||
|
|
|
|
|
|
|
|
|||||
17. Найти матрицу C A 2B , если |
|
1 |
2 |
|
4 |
5 |
|
: |
|
|||
|
|
|
|
|
|
|
|
|
||||
A |
2 |
|
, |
B |
7 |
|
|
|
||||
|
|
|
|
3 |
|
6 |
|
|
|
|||
7 |
8 |
|
|
|
|
|
|
|
|
|
|
|
А) C |
9 |
|
|
|
|
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
3 |
4 |
|
|
|
|
||
|
|
|
|
2 |
|
, |
B |
: |
|
|
|||||
18. Найти произведение матриц A и B , если A |
|
|
1 |
1 |
|
|
|
||||||||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A) неперемножаются |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
19. Произведение матриц А 4 0 |
4 и |
|
|
|
3 |
|
, если эта операция возможна, равно: |
||||||||
B |
|
||||||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A) 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
20. Найдите произведение матриц A и B , если |
A |
2 |
|
1 |
, B |
|
1 |
0 |
: |
||||||
|
1 |
|
4 |
|
|
3 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|||
1 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
13 |
16 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
21.Квадратная матрица A называется неособенной, если :
A)∆A ≠ 0
22.Обратная матрица A 1 для квадратной матрицы 2-го порядка A находится по формуле:
A) |
1 |
|
|
1 A11 |
A21 |
|
|
|
|
|
|
|
|
|||||
A |
|
|
|
|
|
A |
A |
|
|
|
|
|
|
|
|
|
||
|
|
A |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
12 |
22 |
|
|
|
|
|
|
|
|
|
||
23. Найти обратную матрицу A 1 , если |
1 |
|
2 |
|
: |
|
|
|
||||||||||
A |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
A) |
|
|
9 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
4 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
24. Для квадратной матрицы 2-го порядка A |
1 |
|
2 |
найти |
A 1 : |
|||||||||||||
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
-3 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

Документ СМК |
Ф 11/13-1.05-2013 |
|
|
|
|
Тестовое задание |
Редакция 3 |
|
Дата введения 01.09.2013 |
|
|
|
|
25. Обратная матрица A 1 для квадратной матрицы 3-го порядка A находится по формуле:
|
1 |
A11 |
A21 |
A31 |
|
A) À 1 |
A |
A |
A |
|
|
|
|
||||
|
|
12 |
22 |
32 |
|
|
À A |
A |
A |
|
|
|
|
13 |
23 |
33 |
|
26.Система линейных алгебраических уравнений называется совместной, если она имеет: A)хотя бы одно решение
27.Совместная система линейных алгебраических уравнений, если имеет только одно решение, называется:
A) Определенной
28.Система линейных алгебраических уравнений всегда имеет решение, если.. A) определитель системы отличен от нуля
29.Решение СЛАУ из 3-х уравнений с 3 неизвестными x1, x2 , x3 находится по формулам Крамера:
А) x |
x1 |
, |
x |
x2 |
, |
x |
x3 |
|
|
|
|
||||||
1 |
A |
|
2 |
A |
|
3 |
A |
|
|
|
|
|
|
||||
30. Решение матричного уравнения A X B , где A 0 определяется по формуле: |
||||||||
A) X A |
|
1 B |
|
|
|
|
|
|
31. |
Элементарные преобразований системы линейных алгебраических уравнений |
||
применяют: |
|
|
|
А) при решении СЛАУ методом Гаусса |
|||
|
x 2y z 2 |
|
|
32. |
|
2x 2 |
. Найти значение z из системы: |
Дана СЛАУ |
|||
|
|
3x y z 8 |
|
|
|
|
|
A) 3 (x=1;y=2;z=3)
2x y z 1
33. Найти значение , решив СЛАУ x 2y 3z 5 :
x 3y 4z 6
A) -1 (x=1;y=-1;z=2)

|
Документ СМК |
|
|
|
|
|
|
|
|
|
|
|
Ф 11/13-1.05-2013 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тестовое задание |
|
|
|
|
|
|
|
|
|
|
|
Редакция 3 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
Дата введения 01.09.2013 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x y 0 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
34. Найти значение x , решив СЛАУ 2y z 1: |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z 2 |
|
|
|
|
|
||||
A) x |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
x |
2x |
2 |
|
|||||
|
35. Найти значение x1 |
|
|
|
|
1 |
|
|
2 |
|
3 |
|
|
||||||
|
, решив СЛАУ x2 |
2x3 |
3 |
: |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
0 |
|
|
||
|
|
|
|
|
|
|
|
|
|
x |
2 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
A) x1 |
3 (x2=1;x3=1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
x1 x3 1 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
2x2 |
x3 |
0 : |
|
|
|
|
|
||||
|
36. Найти решение СЛАУ x1 |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
x |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
; |
1 |
; |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A) |
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
x |
x |
2 |
|
|
|||||
|
37. Найти значение x2 |
|
|
|
|
1 |
|
|
3 |
|
|
|
|
|
|||||
|
, решив СЛАУ x1 |
x2 x3 6 : |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
x |
3x |
5 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
3 |
|
|
|
|
A) x2 2 (x1=3;x2=2)
|
|
|
|
|
3x 4y 11 |
|
38. |
|
|
|
|
|
28 : |
Найти значение x , решив СЛАУ 5y 6z |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
x 2z 7 |
|
A) x=1 (y=2;z=3) |
|
|
|
|
||
|
|
4x 5z 8 |
|
|
|
|
39. |
Дана СЛАУ |
|
|
|
|
|
2x y 2z 3 . Найти x |
|
|||||
|
|
|
|
|
|
|
|
|
x 3y 1 |
|
|
|
|
A) x 2 |
|
|
|
|
|
|
|
|
|
,b2 |
,b3 |
|
|
40. |
Если a a1,a2 |
,a3 и b b1 |
коллинеарные векторы, тогда |
|||
А) 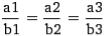
Документ СМК |
Ф 11/13-1.05-2013 |
|
|
|
|
Тестовое задание |
Редакция 3 |
|
Дата введения 01.09.2013 |
|
|
|
|
41. Условие ортогональности двух векторов a и b :
A) a*b=0 (не х)
|
|
|
|
|
||
42. Как расположены ненулевые векторы a |
и b , если |
a b |
a |
|
b |
: |
A) |
|
|
|
|
|
|
43.Векторы, лежащие на одной прямой или на параллельных прямых называются.. A) коллинеарными
44.Векторы, расположенные в одной плоскости или параллельные одной и той же плоскости называются..
A) компланарными
45.Разложение вектора a по базису i , j,k в пространстве имеет вид:
А) a axi ay j az k
46.Направляющие косинусы вектора a , заданного в пространстве находятся по формулам:
А) cosa= |
ax |
,cos B= |
ay |
|
,cosy= |
az |
|
|
|
||||||||||||||
|
a |
|
|
|
a |
|
|
|
|
a |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a1,a2 ,a3 |
b1,b2 ,b3 |
определяется по формуле: |
||||||
47. Угол между векторами a |
и b |
||||||||||||||||||||||
А) cos |
|
|
|
|
axbx ayby azbz |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a 2 |
a |
2 a 2 |
|
|
|
|
b 2 |
b 2 |
b 2 |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
x |
y |
z |
|
|
|
|
|
|
x |
y |
|
|
z |
|
|
|
||||
48.Дан вектор a 3i 4 j 5k в виде разложения по базису i , j,k . Укажите аппликату этого вектора:
A)5
49.Указать абсциссу единичного вектора для вектора a 3, 2, 1 :
A)143
50 Дан вектор b(1;1;0) . Косинус угла между вектором b и осью OY равен:

Документ СМК |
Ф 11/13-1.05-2013 |
|
||
|
|
|
|
|
Тестовое задание |
Редакция 3 |
|
||
Дата введения 01.09.2013 |
|
|||
|
|
|
|
|
A) |
1 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
51.Найдите координаты вектора M1M2 , если M1 (1;3), M 2 ( 5;6) : A) (-6;3)
52.Вычислить модуль вектора a(2;3;6) :
A)7
53.Укажите координаты единичного вектора BA0 , если известны координаты точек A 2,3 и
B 1,2 :
A) |
|
3 |
, |
|
1 |
|
||||||||
|
|
|
|
|
||||||||||
10 |
|
10 |
||||||||||||
|
|
|
|
|
||||||||||
54. |
Дан вектор a(1; 6;5) . Проекция вектора |
|
|
|
на ось OX равна: |
|||||||||
a |
||||||||||||||
A) 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
55. |
Найти вторую координату вектора a если |
|
a |
|
2 |
|
и первая координата равна 6-ти: |
|||||||
|
|
13 |
||||||||||||
A) a1(6;4), |
a2 (6; 4) |
|||||||||||||
56.Найти коэффициенты разложения вектора a(9;1) по векторам u(2;1) и v(1;0) : A) a=u+7v
57.Разложите вектор d 2; 3 по векторам a 1;0 и b 2;3 :
A)d 4a b
|
2; |
|
1; |
|
|
|
58. Даны векторы a |
6 , b |
. При каком значении коэффициента векторы a и |
||||
|
|
|
|
|
|
|
b коллинеарны: |
|
|
|
|
|
|
A) -3 |
|
|
|
|
|
|
|
|
|
|
3; |
|
|
59. Даны векторы a |
1; 2;3 и b |
5;4 . Определить координаты вектора c 3 a |
5 b : |
|||
A) c (18;-31;29)

Документ СМК |
Ф 11/13-1.05-2013 |
|
|
|
|
Тестовое задание |
Редакция 3 |
|
Дата введения 01.09.2013 |
|
|
|
|
60.Даны длины векторов a 3, b 1. Угол между векторами равен 43 . Найти скалярное произведение векторов:
A)3 22
61Даны векторы a(1;2; 2), b(2;3;4), c(0;1;2) . Укажите ортогональные векторы:
A)a и b
62. |
Найдите векторное произведение векторов a i j k |
,b 3i 2 j 4k : |
||
A) 2i-j-k |
|
|
|
|
63. |
Смешанное произведение векторов a 4i j 3k; b 2i 3 j k; |
c i 5k : |
||
A) -60 |
|
|
|
|
64. |
Произведение a b c векторов a i j, b 3k, c 2i 2 j |
равно: |
|
|
A) 0 |
|
|
|
|
65. |
Произведение a b векторов a 2i 3 j 5k; b i 2 j k |
равно: |
|
|
A)a b 7i 3 j k
66.Уравнение прямой с угловым коэффициентом:
A)y kx b
67. |
Условие перпендикулярности прямых, заданных уравнениями y k1 x b1 , |
y k2 x b2 : |
|||
А) |
k1 k2 1 |
|
|
||
68. |
Условие параллельности прямых, заданных уравнениями A1x B1x C1 0, |
|
|||
A2 x B2 x C2 0 : |
|
||||
A) |
A1 |
A2 |
C1 |
|
|
B |
|
||||
|
B |
C |
2 |
|
|
|
1 |
2 |
|
|
|
69. Написать формулу, определяющую угол между двумя прямыми y k1x b1 и y k2 x b2 :

Документ СМК |
Ф 11/13-1.05-2013 |
|
|
|
|
Тестовое задание |
Редакция 3 |
|
Дата введения 01.09.2013 |
|
|
|
|
A)tg | k2 k1 | 1 k1k2
70.Написать уравнение прямой с угловым коэффициентом, проходящей через две точки
A 4; 2 и B 3; 1 :
A)y=-3x+10
71.Найти угловой коэффициент прямой 5x 4y 2 0:
A)54
72.Найти расстояние между прямыми 3x 4y 2 0 и 3x 4y 7 0:
A) 59
73. Вычислить площадь треугольника, отсекаемого прямой 3x 4y 12 0 от координатного угла:
A) 6
74. Написать общее уравнение перпендикулярной линии проходящей через середину AB ,
если A 2; 3 , B 3; 5 : A) 2x-4y-21=0
75. Даны две точки на отрезке A 0; 5 и B 4;7 . Найдите на этом отрезке точку делящую его в отношении 3:
A) (3;4)
76.Даны точки C 0; 5 и D 1;5 . Найдите координаты середины отрезка CD :
A)(0,5; 5)
77.Составьте уравнение прямой, проходящей через точку M 2;3 параллельно прямой
5x 2y 6 0 :
A)5x-2y-4=0
78.Уравнение прямой, проходящей через две заданные точки A 1;2 , B 2;1 имеет вид:

Документ СМК |
Ф 11/13-1.05-2013 |
|
|
|
|
Тестовое задание |
Редакция 3 |
|
Дата введения 01.09.2013 |
|
|
|
|
A)x 1 y 2 1 1
79.Составить общее уравнение прямой, проходящей через точки A 2,4 и B 3,1 :
A) 3x+5y-14=0
80.Определить значение k , при котором прямые y kx 3 и y 3x 1 будут перпендикулярны:
А) |
|
1 |
|
|
|
|
|
3 |
|
|
|
81. Определить значение k , при котором прямые y kx 5 |
и y |
x |
4 будут параллельны: |
||
|
|||||
|
1 |
|
5 |
|
|
А) |
|
|
|
|
|
|
5 |
|
|
|
|
82 Эксцентриситет эллипса 53 , большая полуось равна 5. Найти расстояние 2c между фокусами:
A)6
83.Определить координаты центра окружности x 2 2 y 1 2 1: A) (-2;1)
84.Определить величину параметра р параболы x2 5y :
А) 52
85. Определить величину параметра р параболы y2 2x: A) 1
86. Определить координаты фокусов гиперболы x2 y2 1:
16 4
А) F1( 2
 5;0), F2 (2
5;0), F2 (2
 5;0)
5;0)
87. Найти эксцентриситет эллипса x2 y2 1:
25 16
А) E= 53
88. В гиперболе оси равны 2a 10 и 2b 8. Найти уравнения асимптот:
