srs-1

§ 0.1. Графический метод

Графический метод - один из простейших методов решения оптимизационных задач. Применяется к задачам с двумя свободными переменными или сводящимся к ним. В начале на координатной плоскости строят область допустимых решений. Затем по критерию, задаваемому целевой функцией, находят наилучший допустимый план.

Линейная задача с двумя независимыми переменными имеет вид:

>

: am;1x1 + am;2x2 bm:

Область допустимых решений этой задачи задана системой линейных неравенств. Целевая функция f также линейна.

Пусть вектор a = (a1; a2) 6= 0. Линейная функция

f = a1x1 + a2x2;

как функция на координатной плоскости Ox1x2, в графической интерпретации есть скалярное произведение

ha; xi = a1x1 + a2x2

вектора a, задающего функцию, на вектор x = (x1; x2), определяющей положение точки на плоскости. Такая геометрическая интерпретация удобна для графического метода.

Определим понятие множества уровня функции в общем случае. Предположим, что в некоторой области арифметического пространства Rn определена функция f = f(x1; x2; : : : ; xn), принимающая вещественные значения. Множеством уровня высоты h называется множество точек, в которых функция принимает значение равное числу h:

f(x1; x2 : : : ; xn) 2 j f(x1; x2 : : : ; xn) = hg:

Множество уровня функции может оказаться пустым, совпадать со всем , состоять из конечного числа точек и так далее. Любое замкнутое множество в Rn является множество уровня непрерывной функции. Вид множества уровня зависит от функции f и значения параметра h.

Вернемся к линейным функциям на плоскости. Если a = (a1; a2) 6= 0, то точка плоскости с координатами (x1; x2) принадлежит множеству уровня линейной функции f = a1x1 + a2x2 высоты h, если и только если выполняется равенство

a1x1 + a2x2 = h:

Это уравнение определяет прямую линию на плоскости [1].

Каждая точка x1 = (x11; x12) плоскости Ox1x2 лежит на некоторой линии уровня функции f = a1x1 + a2x2. В самом деле, положим h1 = a1x11 + a2x12. Тогда координаты точки x1 удовлетворяют уравнению

a1x1 + a2x2 = h1;

что означает ее принадлежность множеству уровня функции f = a1x1 + a2x2 высоты h1.

Две линии уровня функции f = a1x1 + a2x2 различных высот h1 и h2 не имеют общих точек. Действительно, система уравнений

a1x1 + a2x2 = h1; a1x1 + a2x2 = h2:

при h1 6= h2 не имеет решений. Следовательно, прямые уровней функции f = a1x1 + a2x2 различных высот параллельны.

Пусть (x11; x12) и (x21; x22) - две различные точки плоскости Ox1x2. Каждая из них принадлежит некоторой линии уровня функции f = a1x1 + a2x2. Не трудно заметить, что высота первой линии уровня равна h1 = a1x11 + a2x12, а второй - h2 = a1x21 + a2x22. Отсюда вытекает, что

h2 h1 = a1(x21 x11) + a2(x22 x12) = ha; x2 x1i:

Если точки точки принадлежат одной линии уровня, то h1 = h2 и

ha; x2 x1i = 0:

Следовательно, каждая линия уровня перпендикулярна вектору a = (a1; a2). Если линия уровня высоты h2 получена из линии уровня высоты h1 параллельным переносом в направлении вектора a, то косинус угла между векторами a и x2 x1 будет положительным. Отсюда

h2 h1 = ha; x2 x1i = jajjx1 x2j cos > 0:

4

0.1. Графический метод

Если линия уровня высоты h2 получена из линии уровня высоты h1 параллельным переносом в направлении противоположном вектору a, то косинус угла между векторами a и x2 x1 будет отрицательным и

h2 h1 = ha; x2 x1i = jajjx1 x2j cos < 0:

Подведем итоги:

1)Множество уровня любой высоты линейной функции f = a1x1 +a2x2 при a = (a1; a2) 6= 0 является прямая линия, определенная в уравнением a1x1 +a2x2 = h, где h - высота уровня.

2)Прямая линия уровня a1x1 + a2x2 = h перпендикулярна вектору a = (a1; a2).

3)Прямые линий уровня различных высот параллельны друг другу.

4)При параллельном смещении линии уровня в направлении вектора a высота уровня возрастает, а в противоположном убывает.

5)Линия уровня a1x1 + a2x2 = h разбивает плоскость на две полуплоскости, в одной из которых координаты точек, не лежащих на линии уровня, удовлетворяют неравенству a1x1 + a2x2 < h, а в другой противоположному.

Пример 0.1. Решим графическим методом задачу

f = 3x1 + 3x2 ! max

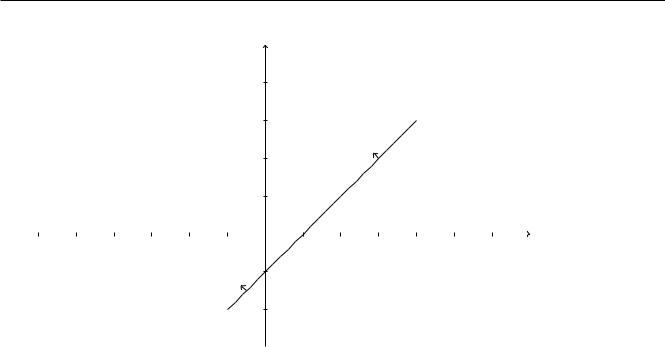
Построим область допустимых решений, определенную системой неравенств. Множество точек, координаты которых удовлетворяют неравенству x1 x2 1, является полуплоскостью, ограниченной прямой x1 x2 = 1. Присвоим этой прямой номер (1). Через каждые две различные точки на плоскости проходит ровно одна прямая линия. Поэтому для того чтобы построить прямую (1) на плоскости, достаточно найти две различные точки этой прямой, а затем соединить их прямой линией. В уравнении первой прямой одну из координат искомой точки можно задать произвольно, а вторую вычислить исходя из уравнения. Возьмем x1 = 0. Тогда x2 = 1. Итак, (0; 1) - первая точка прямой (1). Координата x2 этой точки отлична от нуля. Поэтому, если мы выберем x2 = 0, то получим еще одну точку на этой прямой. Повторяя вычисления, находим точку (1; 0). Теперь, соединив прямой линией эти две точки, получаем чертеж представленный на рисунке 1. Прямая линия (1) разбивает плоскость на две полуплоскости,

5

x2

4

2

1

1

2

Рис. 1: Пример 0.1. Полуплоскость x1 x2 1.

в одной из которых координаты точек, не лежащих на прямой (1), удовлетворяют неравенству x1 x2 < 1, а в другой x1 x2 > 1. Для того чтобы выбрать нужную полуплоскость возьмем пробную точку x0, лежащую внутри одной из полуплоскостей, и подставим ее координаты в левую часть неравенства. Выберем x0 = (0; 0). Тогда x01 x02 = 0 0 = 0 < 1. Следовательно, полуплоскость содержащая точку x0 является искомой. На рисунке 1 ее положение отмечено стрелками, направленными от прямой (1) в сторону полуплоскости.

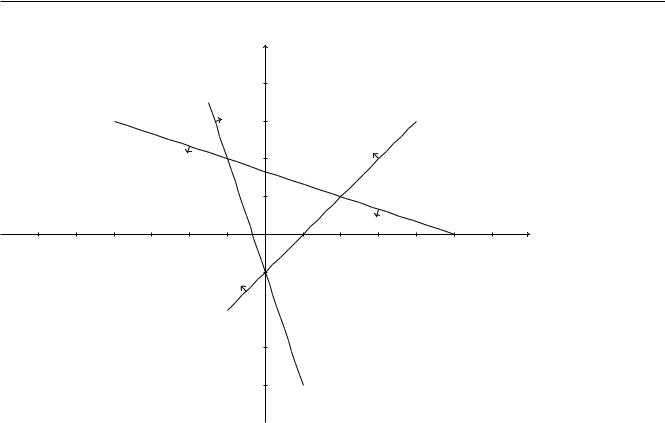
Аналогичные построения, проведенные со вторым и третьим неравенствами, приводят к чертежу, изображенному на рисунке 2

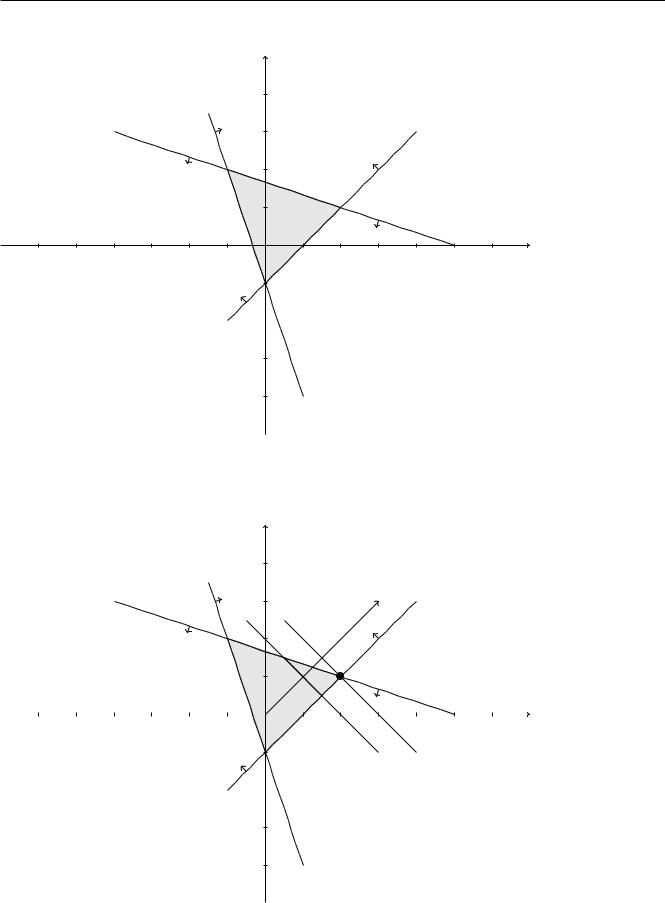
Область допустимых решений - общая часть выделенных полуплоскостей. На чертеже рисунка 3 она выделена штриховкой.

Теперь для того чтобы решить задачу, нужно найти точки уровня целевой функции f = 3x1 + 3x2 максимальной высоты в полученной области допустимых решений. Множество уровня - прямая линия перпендикулярная вектору a = (3; 3). Занесем вектор на чертеж и построим какую-нибудь линию уровня целевой функции, пересекающую область допустимых решений.

На чертеже, расположенном на рисунке 4, линия проведена через точку (2; 0). Поэтому высота уровня равна 2. Точки отрезка AB принадлежат области допустимых решений и расположены на уровне высоты 2. Для того чтобы увеличить высоту нужно параллельно перемещать линию уровня в направлении вектора a = (3; 3). В крайнем положении на линии уровня осталась одна точка.

6

0.1. Графический метод

2

3

4 (3)

Рис. 2: Пример 0.1. Полуплоскости: (1) x1 x2 1, (2) x1 + 5x2 5 и (3) 3x1 + x2 1.

Обозначим ее через xmax, найдем координаты и соответствующую высоту уровня целевой функции. Точка xmax является точкой пересечения прямых (1) и (2). Поэтому ее координаты удовлетворяют системе уравнений

Решая которую, получаем xmax = (2; 1). Далее,

fmax = f(xmax) = 3 2 + 3 1 = 9:

Ответ: xmax = (2; 1) и fmax = 9:

Пример 0.2. Решим графическим методом задачу

f = x1 + 4x2 ! min

2x1 + x2 2; x1 0:

Прямая линия (1), заданная уравнением 2x1 + x2 = 2, проходит через точки (1; 0) и (0; 2). Если для выбора полуплоскости, определяемой неравенством

7

2

3

4 (3)

Рис. 3: Пример 0.1. Область допустимых решений.

2

3

4 (3)

Рис. 4: Пример 0.1. Оптимальное решение точка xmax.

8

0.1. Графический метод

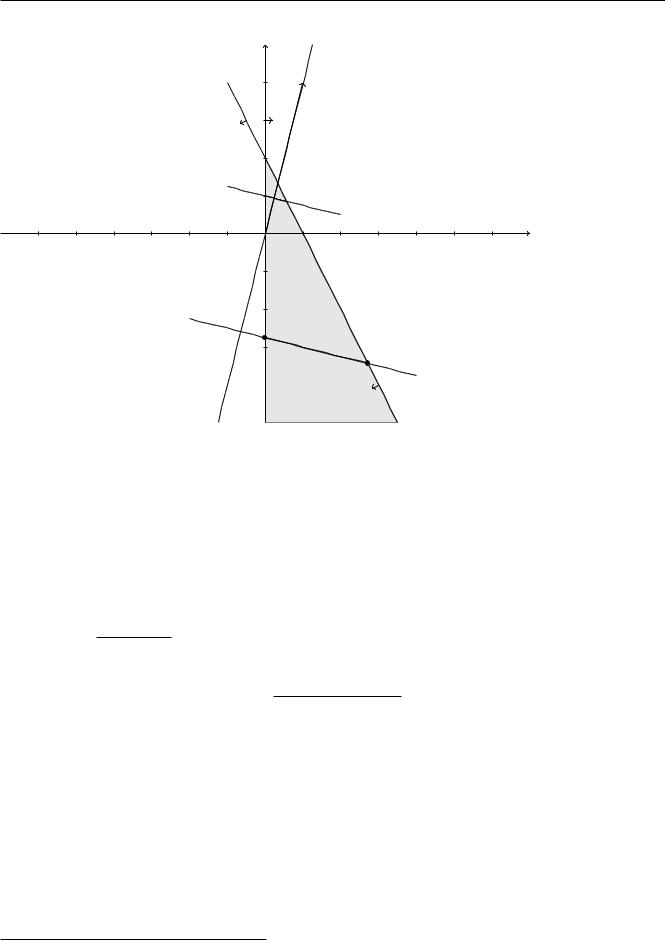
2x1 + x2 2 в качестве пробной точки x0 взять начало координат, то получим, что 2x01 + x02 = 0 < 2. Следовательно, неравенство выделяет полуплоскость содержащую начало координат. Аналогично, линия, определенная уравнением x1 = 0, является координатной осью Ox2, неравенство x1 0 выделяет правую полуплоскость. Область допустимых решений в этой задаче есть угол, отмеченный на рисунке 5 штриховкой. Занесем на чертеж вектор a = (1; 4), ассоциированный с целевой функцией. Линии уровня целевой функции ортогональны этому вектору. Возьмем точку A(t) = (0; t). При любом t 2 точка A(t) принадлежит области допустимых решений. Точка расположена на уровне высоты h(t) = 0+4t = 4t целевой функции. Все точки пересечения прямой 2x1 +x2 = 4t и области допустимых решений, очевидно, расположены на этом уровне. На чертеже рисунка, в геометрических терминах, это есть отрезок [A(t); B(t) прямой линии, перпендикулярной вектору a и проходящей через точку A(t) . Теперь, если в выражении для высоты уровня перейти к пределу при t ! 1, то получим

Таким образом задача решения не имеет, так как ее целевая функция не ограничена снизу на области допустимых решений. Условимся отсутствие решения в задаче минимизации по причине неограниченности целевой функции записывать в виде: fmin = 1. =

(0; 2); fmax = 8. Проверьте.

Ответ: fmin = 1.

Как уже отмечалось выше для любого замкнутого множества в арифметическом пространстве Rn найдется непрерывная во всем пространстве функция, для которой это множество является множеством уровня нулевой высоты. Если функция f = f(x1; x2), определенная на открытом множестве R2, непрерывна в каждой точке и имеет в ней непрерывные частные производные, причем градиент функции

то вследствие теоремы о неявной функции [2] множество уровня, проходящего через любую точку x0 = (x01; x02) области определения функции, локально является линией, которая представима как график непрерывно дифференцируемой функции либо вида y = (x), либо вида x = (y).

Уровни функции, соответствующие различным значениям высоты, не имеют общих точек. В самом деле, значение любой функции в точке однозначно определено, поэтому система уравнений

f(x1; x2) = h1; f(x1; x2) = h2:

9

2

A(t)

3 B(t)

4

(1)

Рис. 5: Пример 0.2. Графическая иллюстрация.

при h1 6= h2 не имеет решений.

p

где j xj = x21 + x22. Сравнение g = o(j xj) означает, что остаток g = g(x01; x02; x1; x2)

удовлетворяет условию:

lim g(x01; x02; x1; x2) = 0:

j xj!0 j xj

По предположению градиент rf(x01; x02) отличен от нулевого. Поэтому малое перемещение точки в направлении вектора rf(x01; x02) или направлении , составляющем с ним острый угол, приводит к росту значения функции, а в направлении противоположном или составляющем с градиентом тупой угол, приводит к уменьшению значения.

При решении нелинейных задач математического программирования возникает вопрос об определении высоты множества точек уровня функции f(x1; x2) и точки его касания с границей множества допустимых решений, заданной уравнением g(x1; x2) = 0. Предположим, что в рассматриваемой области один раз непрерывно дифференцируемы и их градиенты отличны от нулевого вектора. В точке касания линии уровня функции f(x1; x2) с кривой эти линии имеют общую касательную. Ненулевой вектор (p; q), направление которого совпадает с

1Тейлор, Брук - английский математик, 1685-1735.

10

0.1. Графический метод

направлением общей касательной, ортогонален обоим градиентам. Поэтому в точке касания (x01; x02) выполняются равенства

fx1 (x01; x02)p + fx2 (x01; x02)q = 0; gx1 (x01; x02)p + gx2 (x01; x02)q = 0:

Из этих равенств, в частности, следует, что однородная система из двух линейных алгебраических уравнений

fx1 (x01; x02)y1 + fx2 (x01; x02)y2 = 0; gx1 (x01; x02)y1 + gx2 (x01; x02)y2 = 0:

относительно двух неизвестных y1 и y2 имеет ненулевое решение: y1 = p и y2 = q. По правилу Крамера2 если определитель матрицы коэффициентов квадратной системы линейных алгебраических уравнений отличен от нуля, то эта система имеет единственное решение. Для рассматриваемого случая - нулевое: y1 = 0 и y2 =). Следовательно, определитель системы равен нулю:

fx1 (x01; x02)gx2 (x01; x02) fx2 (x01; x02)gx1 (x01; x02) = 0:

Отсюда вытекает, что координаты (x1; x2) точки касания и высота уровня h удовлетворяют системе уравнений

8

<fx1 (x1; x2)gx2 (x1; x2) fx2 (x1; x2)gx1 (x1; x2) = 0; g(x1; x2) = 0;

: f(x1; x2) = h:

Верно и обратное: если (x1; x2) и h - решение последней системы, то в точке (x1; x2) кривая, заданная уравнением g(x1; x2) = 0, касается линии уровня Mh = f(x1; x2)jf(x1; x2) = hg.

Пример 0.3. Графическим методом решим задачу о нахождении наибольшего и наименьшего значений функции f = (x1 1)2 + x22 на множестве, определяемом системой неравенств:

Областью допустимых решений является треугольник на чертеже рисунка 6, образованный полуплоскостями, заданными неравенствами из условий задачи. Множества уровней целевой функции f = (x1 1)2 + x22 высоты h:

f(x1; x2) j (x1 1)2 + x22 = hg = Mh

пусты при h < 0. При h = 0 множество уровняp- точка (1; 0). При h > 0 множество уровня является окружностью радиуса h с центром O в точке (1; 0).

2Крамер, Габриель - швейцарский математик, 1704-1752.

11

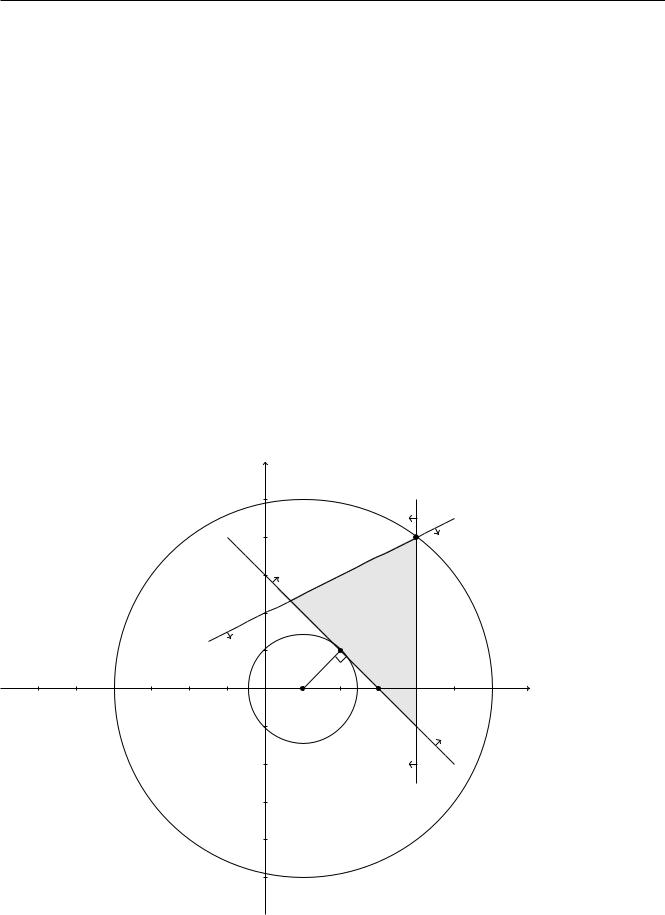
Значение целевой функции в точке (x1; x2) - квадрат расстояния от этой точки до центра окружности. Поэтому, решением задачи минимизации является ближайшая к центру окружности точка области допустимых решений, а задачи максимизации - наиболее удаленная. Для нахождения координат первой из точки O опустим перпендикуляр на прямую (1). Обозначим через A точку пересечения прямой (1) с координатной осью Ox1. Координаты точки легко находятся и равны (3; 0). Треугольник с вершинами в точках xmin, O и A является прямоугольным, с равными углами при гипотенузе. Поэтому точка (2; 0) является одновременно серединой стороны OA и основанием высоты, опущенной из прямого угла. Отсюда следует, что xmin = (2; 1) и fmin = f(xmin) = 2. Точка xmax лежит на пересечении прямых (2) и (3). Поэтому ее координаты удовлетворяют системе уравнений

Отсюда получаем xmax = (4; 4) и fmax = 25.

3

4

5

Рис. 6: Пример 0.3. Графическое решение.

12