6.Расчет области устойчивости
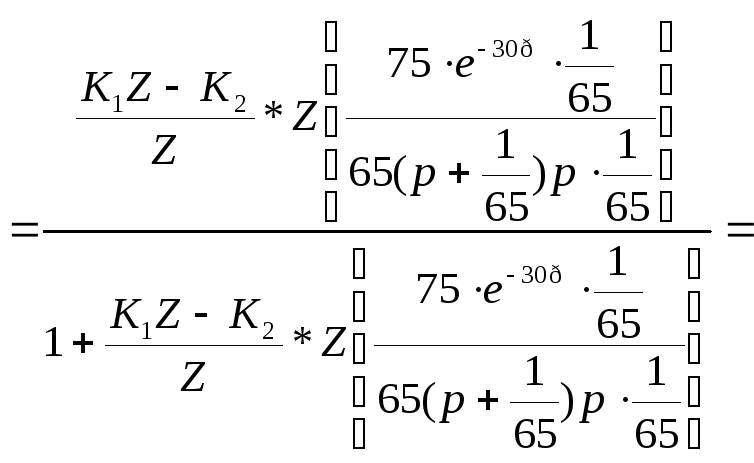
Для расчета области устойчивости воспользуемся критерием Михайлова для дисперсных систем. Рассмотрим характеристический полином замкнутой системы, который как знаменатель передаточной функции замкнутой системы.
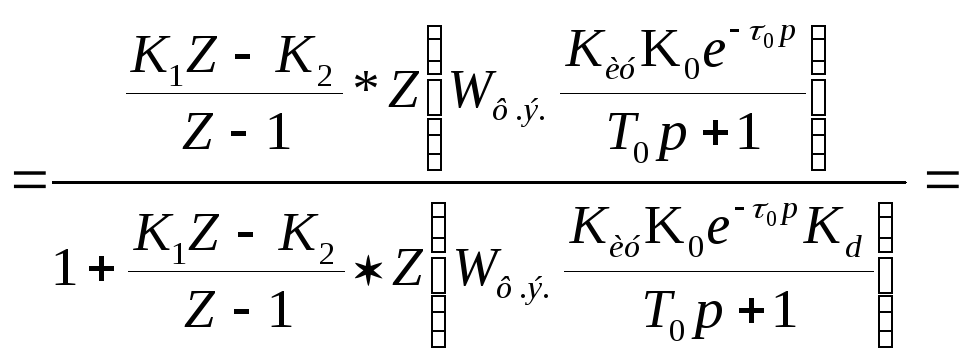
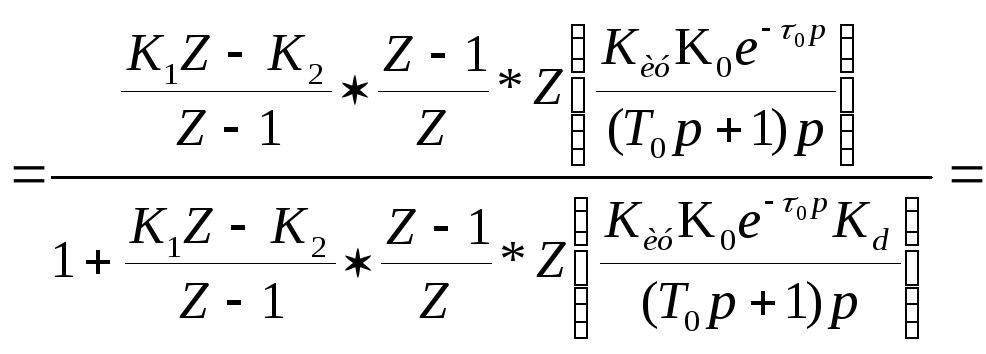
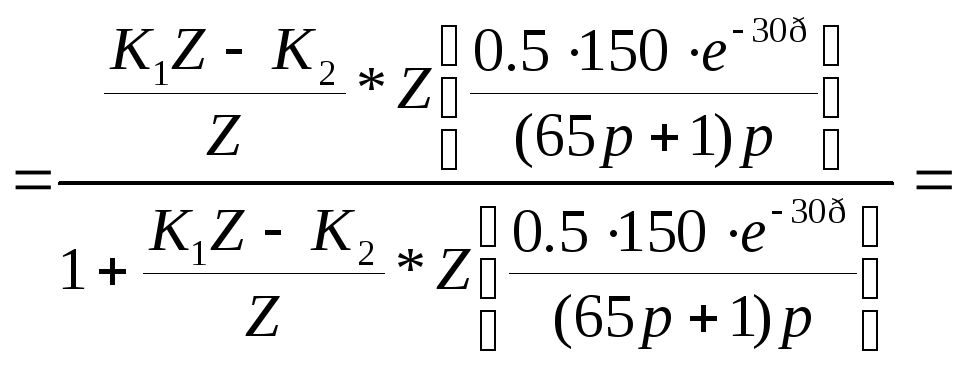
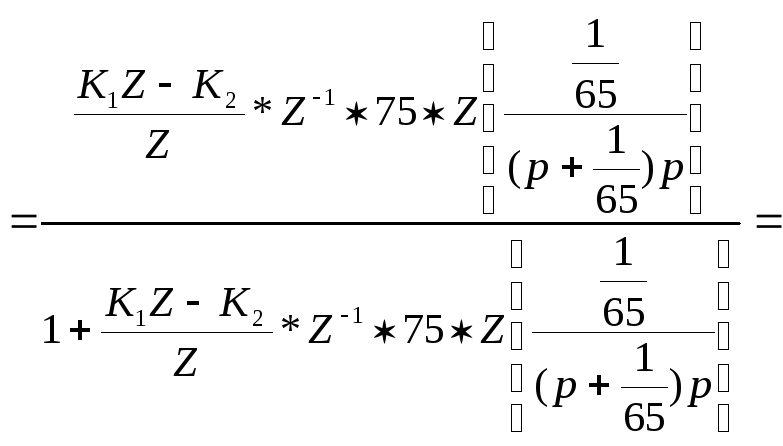
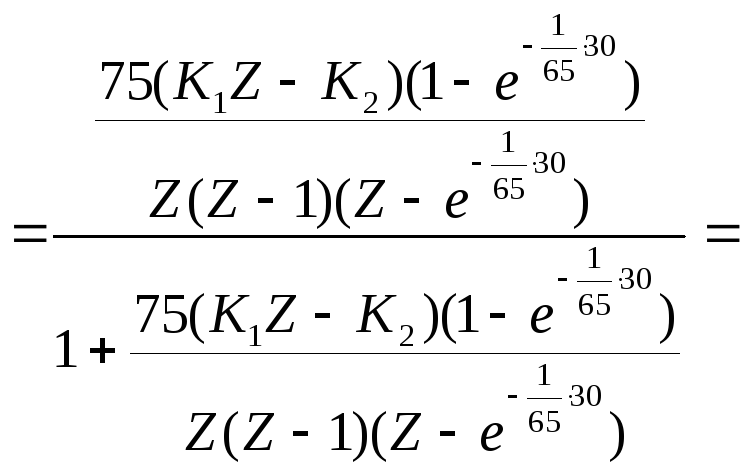
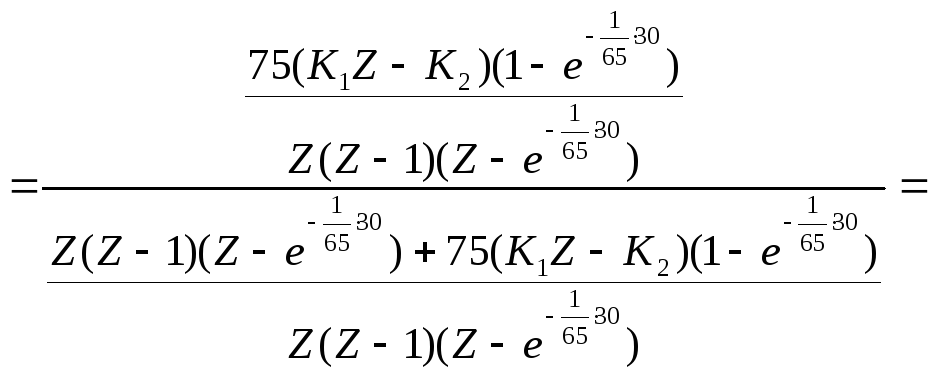
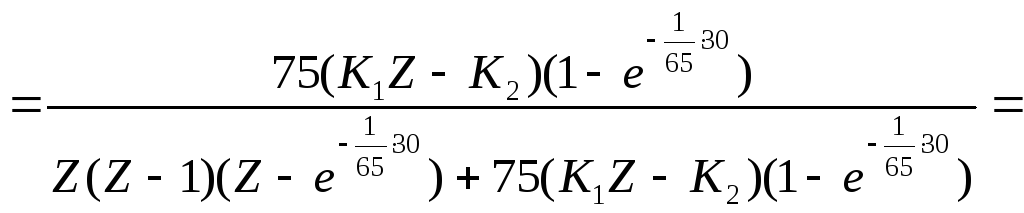
а) апериодическая граница получается из характеристического уравнения при z = 1,что соответствует нулевому значению относительной частоты (ω=0; z = 1)
→ к2 = к1
б)колебательная граница
условия нахождения
колебательной границе состоит в замене
,
по формуле Эйлера и выделением мнимой
и вещественной части из характеристического
уравнения.
D(Z)=
cos3
+jsin3
-1.607cos2
-j1.607sin2
+0.607cos
+j0.607sin
+
+29.5
*cos
+j29.5
*sin
-29.5
=U(
)+JV(
)=0
U(
)=cos3
-1.607cos2
+0.607cos
+29.5
*cos
-29.5
=0
V(
)=sin3
-1.607sin2
+0.607sin
+29.5
*sin
=0
Составим таблицу и построим график области устойчивости
|
ω |
k1 |
k2 |
|
0,01 |
0,013314 |
0,013319 |
|
0,1 |
0,012515 |
0,012983 |
|
0,2 |
0,010142 |
0,011971 |
|
0,3 |
0,006346 |
0,010294 |
|
0,4 |
0,00136 |
0,00797 |
|
0,5 |
-0,00451 |
0,005023 |
|
0,6 |
-0,01088 |
0,00148 |
|
0,7 |
-0,01733 |
-0,00262 |
|
0,8 |
-0,02341 |
-0,00724 |
|
0,9 |
-0,02865 |
-0,01233 |
|
1 |
-0,0326 |
-0,01784 |
|
1,1 |
-0,03484 |
-0,02372 |
|
1,2 |
-0,035 |
-0,02991 |
|
1,3 |
-0,03276 |
-0,03634 |
|
1,4 |
-0,02792 |
-0,04295 |
|
1,5 |
-0,02035 |
-0,04968 |
|
1,6 |
-0,01003 |
-0,05645 |
|
ω |
k1 |
k2 |
|
1,7 |
0,002966 |
-0,06321 |
|
1,8 |
0,018431 |
-0,06988 |
|
1,9 |
0,036072 |
-0,07639 |
|
2 |
0,055499 |
-0,08269 |
|
2,1 |
0,076239 |
-0,0887 |
|
2,2 |
0,097755 |
-0,09437 |
|
2,3 |
0,119461 |
-0,09965 |
|
2,4 |
0,140745 |
-0,10447 |
|
2,5 |
0,16099 |
-0,10879 |
|
2,6 |
0,179596 |
-0,11257 |
|
2,7 |
0,196002 |
-0,11577 |
|
2,8 |
0,20971 |
-0,11835 |
|
2,9 |
0,220295 |
-0,1203 |
|
3 |
0,22743 |
-0,12159 |
|
3,1 |
0,230892 |
-0,12221 |
|
3,14 |
0,23122 |
-0,12227 |
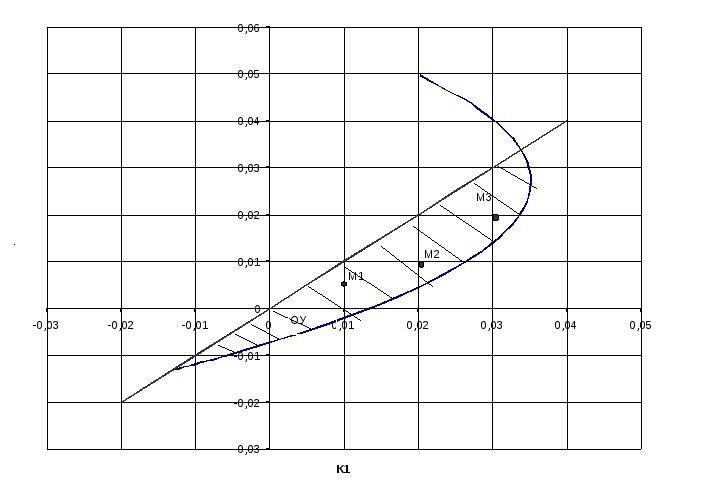М1
(К1=0,01; К2=0,005), М2(К1=0,02; К2=0,01), М3(К1=0,03;
К2=0,02)