Физический (энергетический) смысл уравнения Бернулли

С физической точки зрения уравнение Бернулли представляет собой запись закона сохранения и превращения энергии применительно к движению идеальной жидкости.

Напор — энергия, отнесенная к единице веса жидкости (удельная весовая энергия).

h_ск — удельная кинетическая энергия, h_пз — удельная энергия сил давления, h_г — удельная энергия положения.

Уравнение Бернулли для потока реальной (вязкой) жидкости

При движении реальной жидкости часть энергии теряется на преодоление силы трения между слоями жидкости и местных гидравлических сопротивлений. Из-за наличия сил трения отдельные слои жидкости движутся с разными скоростями. Поскольку поток жидкости можно рассматривать как совокупность отдельных струек, то уравнение Бернулли для потока получается интегрированием энергий отдельных струек и далее делится на массу движущейся жидкости.

Здесь 1 и 2 — рассматриваемые сечения жидкости по мере движения, w_ср — средние скорости в данном сечении, р_цт — давление в центре тяжести живого сечения потока, z_цт — геометрические параметры в центре живого сечения,  — коэффициент, учитывающий распределение скорости по сечению потока.

При движении вязкой жидкости, если режим ламинарный, то коэффициент =2, для турбулентного потока =1,051,08. Поскольку при движении вязких жидкостей чаще наблюдается турбулентный режим, а 1, получим:

Здесь h₁₂ — потерянный напор на участке между 1 и 2 сечениями. Таким образом, чтобы иметь вохможность воспользоваться этим уравнением, нужно рассчитать h₁₂.

88.Уравнение конвективного переноса импульса (уравнение Навье-Стокса)

Локальная форма закона сохранения импульса.

Аналогично законам сохранения массы и энергии можно получить локальную (для точки) форму закона сохранения импульса.

Отличие будет заключаться лишь в векторной природе переносимой субстанции – импульса единичного объема W.(2.57)Здесь:- суммарный поток импульса,

–ускорение.

Если массовая сила есть сила тяжести, то =g.

Расчленив тензор потока импульса  на конвективную часть и тензор вязких напряжений _в по (2.27) , можно представить общий вид уравнения движения с локализованием субстанциональной производной:

(2.58)

Здесь:

Допустив  = const (молекулярная вязкость) для ламинарного движения получим: уравнение Навье-Стокса:: (2.59)

Разделив уравнение (2.59) на  получим привычный вид уравнения Навье-Сток(2.60)

Развернутый вид уравнения (2.60) для оси X в декартовой системе координат имеет следующий вид (2.61)

Остальные уравнения по осям y,z могут быть получены заменой индексов по кругу xyzx.

Рассмотрим частные случаи уравнения Навье-Стокса: Если среда идеальная, то  = 0 и получим:

(2.62) Уравнение Эйлера.

Если среда находится в равновесии, то W = 0 и получим:(2.63) - Уравнение равновесия Эйлера.

89.Уравнение конвективного переноса теплоты (уравнение Фурье-Киргоффа)

Локальная форма закона сохранения энергии.

Локальное уравнение сохранения энергии можно получить для единичного объема следующим образом:

Переносимая субстанция – энергия единичного объема Е. Тогда:

(2.50)

На практике при рассмотрении процесса переноса тепла в изобарных условиях можно пренебречь работой по преодолению сил трения и изменением механической энергии, тогда можно записать:

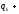
()(2.51)

В этих условиях E = C_pT. Раскрывая выражения иполучим:

В частном случае ламинарного движения и постоянства теплофизических характеристик (C_p, ,  = const, _T = 0)

Это уравнение упрощается:=²T (2.53)Здесь =- коэффициент молекулярной температуропроводности. Распишем уравнение (2.53):