
IPR_1-1 вариант 5
.docxМинистерство образования Республики Беларусь
Учреждение образования «Белорусский государственный университет информатики и радиоэлектроники»
Факультет непрерывного и дистанционного обучения
Кафедра высшей математики
МАТЕМАТИКА, ЧАСТЬ 1
ИНДИВИДУАЛЬНАЯ ПРАКТИЧЕСКАЯ РАБОТА №1-1
«ВЕКТОРНОЕ ИСЧИСЛЕНИЕ. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ. ЛИНЕЙНАЯ АЛГЕБРА»
Вариант : 5
Минск 2017
Задача 1
Даны
два вектора ![]() и
и ![]() ,
выраженные в виде линейной комбинации
векторов
,
выраженные в виде линейной комбинации
векторов ![]() и
и ![]() .
Найдите: а)
.
Найдите: а) ![]() и
и ![]() ;
б) скалярное произведение
;
б) скалярное произведение ![]() ;
в) угол между векторами
;
в) угол между векторами ![]() и
и ![]() ;
г) длину третьей стороны и площадь
треугольника, построенного на
векторах
;
г) длину третьей стороны и площадь
треугольника, построенного на
векторах ![]() и
и ![]() .
.
 -
2
-
2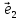 ;
;
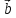 = - 2
= - 2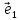 + 5
+ 5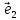 ;
;
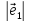 =
2;
=
2;
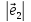 = 3;
= 3;
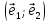 = arc
= arc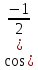 )
)
Решение
а) ![]() и
и ![]()

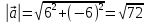
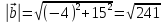
б) скалярное
произведение ![]() ;
;
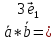 – 2
– 2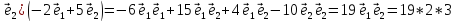 =114.
=114.
в) угол между
векторами ![]() и
и ![]()
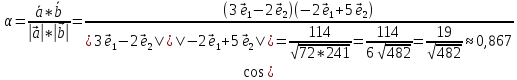

г) длину третьей
стороны и площадь треугольника,
построенного на векторах ![]() и
и ![]()

Найдем векторное произведение векторов

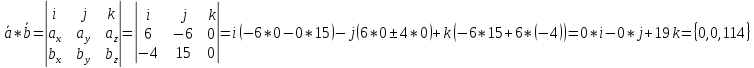
Найдем модуль вектора:
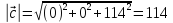
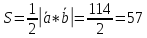
Задача 2
Дана
точка М –
вершина треугольной пирамиды и три
вектора ![]() ,
образующие её боковые рёбра. Найдите:
а) уравнение плоскости основания
пирамиды; б) угол между гранью,
образованной векторами
,
образующие её боковые рёбра. Найдите:
а) уравнение плоскости основания
пирамиды; б) угол между гранью,
образованной векторами ![]() ,
и плоскостью основания; в) угол между
ребром, образованным вектором
,
и плоскостью основания; в) угол между
ребром, образованным вектором ![]() ,
и плоскостью основания; г) уравнение
высоты, опущенной из вершины М на
основание; д) объём пирамиды.
,
и плоскостью основания; г) уравнение
высоты, опущенной из вершины М на
основание; д) объём пирамиды.
М(-4;1;3),
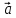 (2;2;5),
b(-1;3;-2),
(2;2;5),
b(-1;3;-2),
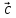 (3;1;1)
Решение
(3;1;1)
Решение
а) уравнение плоскости основания пирамиды;
Для составления уравнения плоскости используем формулу:
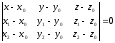 ,
где
,
где
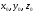 -
координаты точки a,
-
координаты точки a,
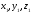 -
координаты точки b,
-
координаты точки b, -
координаты точки c.
-
координаты точки c.
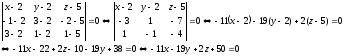
б) угол
между гранью, образованной векторами ![]() ,
и плоскостью основания;
,
и плоскостью основания;
Косинус
угла между плоскостью A1x
+ B1y
+ C1 +
D = 0 и плоскостью A2x
+ B2y
+ C2 +
D = 0 равен углу между их нормальными
векторами N1(A1,
B1,
C1)
и N2(A2,
B2,
C2):
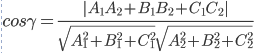 Уравнение
плоскости ABM:
Уравнение
плоскости ABM:
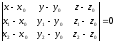 ,
где
,
где
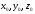 -
координаты точки a,
-
координаты точки a,
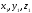 -
координаты точки b,
-
координаты точки b,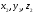 -
координаты точки c.
-
координаты точки c.

-x
+ 4y + z-11 = 0
Уравнение
плоскости
ABC: -11x - 19y + 2z + 50 = 0
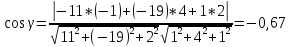 γ
= arccos(-0.67) = 132.071o
γ
= arccos(-0.67) = 132.071o
в) угол
между ребром, образованным вектором ![]() ,
и плоскостью основания;
,
и плоскостью основания;
Синус
угла между прямой с направляющими
коэффициентами (l; m; n) и плоскостью с
нормальным вектором N(A; B; C) можно найти
по формуле:
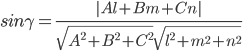 Уравнение
плоскости ABC: -11x - 19y + 2z + 50 = 0
Уравнение
прямой CM:
Уравнение
плоскости ABC: -11x - 19y + 2z + 50 = 0
Уравнение
прямой CM:
![]()

 γ
= arcsin(0.505) = 30.332o
γ
= arcsin(0.505) = 30.332o
г) уравнение высоты, опущенной из вершины М на основание;
Прямая, проходящая через точку M(x0;y0;z0) и перпендикулярная плоскости Ax + By + Cz + D = 0 имеет направляющий вектор (A;B;C) и, значит, представляется симметричными уравнениями: Уравнение плоскости ABC: -11x - 19y + 2z + 50 = 0
![]()
![]()
д) объём пирамиды
Объем пирамиды, построенный на векторах a1(X1;Y1;Z1), a2(X2;Y2;Z2), a3(X3;Y3;Z3) равен:
|
|
|
|
|
|
|
Находим определитель матрицы
∆ = (-3) • ((-1) • (-2)-(-1) • (-4))-1 • (1 • (-2)-(-1) • (-7))+(-6) • (1 • (-4)-(-1) • (-7)) = 81
Задача 3
Найдите
координаты точки M',
симметричной точке M(2;1;0)
относительно прямой 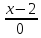 =
=
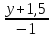 =
=
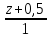
Решение
Находим уравнение плоскости, которая перпендикулярна данной прямой и проходит через точку М.Так как плоскость перпендикулярна заданной прямой, то в качестве ее вектора нормали можно взять направляющий вектор прямой:
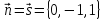
Тогда уравнение искомой плоскости:

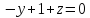

Найдем точку М0 пересечения прямой и плоскости. Запишем параметрические уравнения прямой.
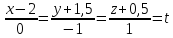
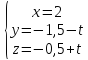
Подставляем в уравнение плоскости:
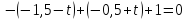
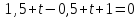
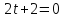
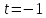
Найдем координаты точки пересечения прямой и плоскости:
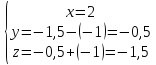
Получаем М0(2; -0,5;-1,5)
Так как М0 является серединой отрезка ММ', то
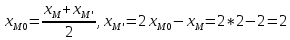
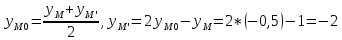
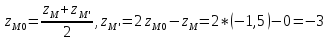
Получаем М'(2; -2; -3)
Задача 4
Составьте
уравнение кривой, модуль разности
расстояний от каждой точки которой до
точек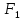 (0;-5),
(0;-5),
 (0;5)равен
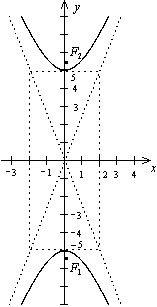
6. Приведите это уравнение к каноническому
виду, определите тип кривой и постройте
её.
(0;5)равен
6. Приведите это уравнение к каноническому
виду, определите тип кривой и постройте
её.
Решение
Гипербола
- множество точек M плоскости,
для каждой из которых модуль разности
расстояний от точек ![]() и
и ![]() равен 2a.
Точки
равен 2a.
Точки ![]() и
и ![]() называются
фокусами гиперболы;
называются
фокусами гиперболы; ![]() -
действительная ось;
-
действительная ось; ![]() -
мнимая ось; O -
центр;
-
мнимая ось; O -
центр; ![]() -
левый и правый фокусы;
-
левый и правый фокусы; ![]() -
вершины;
-
вершины; ![]() -
фокальные радиусы:
-
фокальные радиусы: ![]()
Каноническое
уравнение: 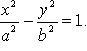

Pасстояние
между фокусами гиперболы равно
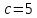
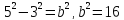
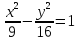
Задача 5
Вычислите определитель 5-го порядка методом Гаусса.
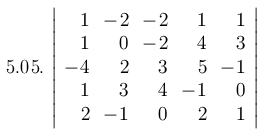
Решение
Запишем матрицу в виде:
|
1 |
-2 |
-2 |
1 |
1 |
|
1 |
0 |
-2 |
4 |
3 |
|
-4 |
2 |
3 |
5 |
-1 |
|
1 |
3 |
4 |
-1 |
0 |
|
2 |
-1 |
0 |
2 |
1 |
Работаем со столбцом №1
Умножим 4-ю строку на (k = -2 / 1 = -2) и добавим к 5-й:
|
1 |
-2 |
-2 |
1 |
1 |
|
1 |
0 |
-2 |
4 |
3 |
|
-4 |
2 |
3 |
5 |
-1 |
|
1 |
3 |
4 |
-1 |
0 |
|
0 |
-7 |
-8 |
4 |
1 |
Умножим 3-ю строку на (k = 1 / 4 = 1/4) и добавим к 4-й:
|
1 |
-2 |
-2 |
1 |
1 |
|
1 |
0 |
-2 |
4 |
3 |
|
-4 |
2 |
3 |
5 |
-1 |
|
0 |
7/2 |
19/4 |
1/4 |
-1/4 |
|
0 |
-7 |
-8 |
4 |
1 |
Умножим 2-ю строку на (k = 4 / 1 = 4) и добавим к 3-й:
|
1 |
-2 |
-2 |
1 |
1 |
|
1 |
0 |
-2 |
4 |
3 |
|
0 |
2 |
-5 |
21 |
11 |
|
0 |
7/2 |
19/4 |
1/4 |
-1/4 |
|
0 |
-7 |
-8 |
4 |
1 |
Умножим 1-ю строку на (k = -1 / 1 = -1) и добавим к 2-й:
|
1 |
-2 |
-2 |
1 |
1 |
|
0 |
2 |
0 |
3 |
2 |
|
0 |
2 |
-5 |
21 |
11 |
|
0 |
7/2 |
19/4 |
1/4 |
-1/4 |
|
0 |
-7 |
-8 |
4 |
1 |
Работаем со столбцом №2
Умножим 4-ю строку на (k = 7 / 7/2 = 2) и добавим к 5-й:
|
1 |
-2 |
-2 |
1 |
1 |
|
0 |
2 |
0 |
3 |
2 |
|
0 |
2 |
-5 |
21 |
11 |
|
0 |
7/2 |
19/4 |
1/4 |
-1/4 |
|
0 |
0 |
3/2 |
9/2 |
1/2 |
Умножим 3-ю строку на (k = -7/2 / 2 = -7/4) и добавим к 4-й:
|
1 |
-2 |
-2 |
1 |
1 |
|
0 |
2 |
0 |
3 |
2 |
|
0 |
2 |
-5 |
21 |
11 |
|
0 |
0 |
27/2 |
-73/2 |
-39/2 |
|
0 |
0 |
3/2 |
9/2 |
1/2 |
Умножим 2-ю строку на (k = -2 / 2 = -1) и добавим к 3-й:
|
1 |
-2 |
-2 |
1 |
1 |
|
0 |
2 |
0 |
3 |
2 |
|
0 |
0 |
-5 |
18 |
9 |
|
0 |
0 |
27/2 |
-73/2 |
-39/2 |
|
0 |
0 |
3/2 |
9/2 |
1/2 |
Работаем со столбцом №3
Умножим 4-ю строку на (k = -3/2 / 27/2 = -1/9) и добавим к 5-й:
|
1 |
-2 |
-2 |
1 |
1 |
|
0 |
2 |
0 |
3 |
2 |
|
0 |
0 |
-5 |
18 |
9 |
|
0 |
0 |
27/2 |
-73/2 |
-39/2 |
|
0 |
0 |
0 |
77/9 |
8/3 |
Умножим 3-ю строку на (k = 27/2 / 5 = 27/10) и добавим к 4-й:
|
1 |
-2 |
-2 |
1 |
1 |
|
0 |
2 |
0 |
3 |
2 |
|
0 |
0 |
-5 |
18 |
9 |
|
0 |
0 |
0 |
121/10 |
24/5 |
|
0 |
0 |
0 |
77/9 |
8/3 |
Работаем со столбцом №4
Умножим 4-ю строку на (k = -77/9 / 121/10 = -70/99) и добавим к 5-й:
|
1 |
-2 |
-2 |
1 |
1 |
|
0 |
2 |
0 |
3 |
2 |
|
0 |
0 |
-5 |
18 |
9 |
|
0 |
0 |
0 |
121/10 |
24/5 |
|
0 |
0 |
0 |
0 |
-8/11 |
Ранг матрицы равен r=5
Определитель матрицы ∆ = 1 • 2 • (-5) • 121/10 • (-8/11) = 88
Задача 6
Решите матричное уравнение.

Решение
Матричное уравнение пишется в виде: A·X = B. Вычислим определитель матрицы А:

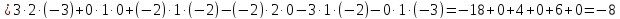
Так как A невырожденная матрица, то существует обратная матрица A-1. Умножим слева обе части уравнения на A-1: A-1·A·X = A-1·B, тогда получим E·X = A-1·B, или X = A-1·B. Найдем обратную матрицу A-1.
Транспонированная матрица AT.
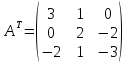
Алгебраические дополнения
∆1,1= (2*(-3) - 1*(-2)) = -4
∆1,2 = -(0*(-3) - (-2)*(-2)) = 4
∆1,3 = (0*1 - (-2)*2) = 4
∆2,1 = -(1*(-3) - 1*0) = 3
∆2,2 = (3*(-3) - (-2)*0) = -9
∆2,3 = -(3*1 - (-2)*1) = -5
∆3,1 = (1*(-2) - 2*0) = -2
∆3,2 = -(3*(-2) - 0*0) = 6
∆3,3 = (3*2 - 0*1) = 6 Обратная матрица A-1.
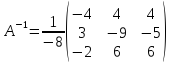
Матрицу Х ищем по формуле: X = A-1·B
