IPR_1-1 вариант 5

c₁₁ = a₁₁ · b₁₁ + a₁₂ · b₂₁ + a₁₃ · b₃₁ = (-4) · (-14) + 4 · 2 + 4 · (-12) = 56 + 8 - 48 = 16 c₁₂ = a₁₁ · b₁₂ + a₁₂ · b₂₂ + a₁₃ · b₃₂ = (-4) · 0 + 4 · 3 + 4 · (-7) = 0 + 12 - 28 = -16 c₁₃ = a₁₁ · b₁₃ + a₁₂ · b₂₃ + a₁₃ · b₃₃ = (-4) · (-11) + 4 · (-2) + 4 · (-3) = 44 - 8 - 12 = 24 c₂₁ = a₂₁ · b₁₁ + a₂₂ · b₂₁ + a₂₃ · b₃₁ = 3 · (-14) + (-9) · 2 + (-5) · (-12) = (-42) - 18 + 60 = 0 c₂₂ = a₂₁ · b₁₂ + a₂₂ · b₂₂ + a₂₃ · b₃₂ = 3 · 0 + (-9) · 3 + (-5) · (-7) = 0 - 27 + 35 = 8 c₂₃ = a₂₁ · b₁₃ + a₂₂ · b₂₃ + a₂₃ · b₃₃ = 3 · (-11) + (-9) · (-2) + (-5) · (-3) = (-33) + 18 + 15 = 0 c₃₁ = a₃₁ · b₁₁ + a₃₂ · b₂₁ + a₃₃ · b₃₁ = (-2) · (-14) + 6 · 2 + 6 · (-12) = 28 + 12 - 72 = -32 c₃₂ = a₃₁ · b₁₂ + a₃₂ · b₂₂ + a₃₃ · b₃₂ = (-2) · 0 + 6 · 3 + 6 · (-7) = 0 + 18 - 42 = -24 c₃₃ = a₃₁ · b₁₃ + a₃₂ · b₂₃ + a₃₃ · b₃₃ = (-2) · (-11) + 6 · (-2) + 6 · (-3) = 22 - 12 - 18 = -8

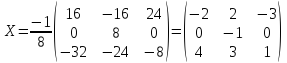
Задача 7

Образует ли заданное множество векторов с естественными операциями сложения и умножения на число линейное пространство?

Решение

Линейным (векторным) пространством называется множество произвольных элементов, называемых векторами, в котором определены операции сложения векторов и умножения вектора на число.

В данном случае, мы имеем прямую и коллинеарные ей вектора. Получаем, что любой вектор выражается через другие вектора (понятие о коллинеарности говорит об этом). Значит мы имеем размерность пространства - 1. Утверждение верно.

Задача 8

В декартовой прямоугольной системе координат заданы вектор  и плоскость р. Найдите: а) вектор  – проекцию вектора  на плоскость р методами аналитической геометрии; б) матрицу геометрического оператора проецирования произвольного вектора на плоскость р и с её помощью координаты вектора 

Решение

Задача 9

Решите систему линейных уравнений по формулам Крамера и методом Гаусса.

Решение.

Метод Крамера

Запишем систему в виде:

Система совместна тогда и только тогда, когда системный (главный) определитель не равен нулю.

Определитель:

(-3)·(-1)·4 + 1·2·2 + (-2)·2·3 - (-2)·(-1)·2 - (-3)·2·3 - 1·2·4 = 12 + 4 - 12 - 4 + 18 - 8 =  10 Заменим 1-ый столбец матрицы А на вектор результата В.

6	1	-2
-3	-1	2
5	3	4

Найдем определитель полученной матрицы. ∆₁ = (-1)^{1 + 1}a₁₁∆₁₁ + (-1)^{2 + 1}a₂₁∆₂₁ + (-1)^{3 + 1}a₃₁∆₃₁ = 6 • ((-1) • 4-3 • 2)-(-3) • (1 • 4-3 • (-2))+5 • (1 • 2-(-1) • (-2)) = -30

Заменим 2-ый столбец матрицы А на вектор результата В.

-3	6	-2
2	-3	2
2	5	4

Найдем определитель полученной матрицы. ∆₂ = (-1)^{1 + 1}a₁₁∆₁₁ + (-1)^{2 + 1}a₂₁∆₂₁ + (-1)^{3 + 1}a₃₁∆₃₁ = (-3) • ((-3) • 4-5 • 2)-2 • (6 • 4-5 • (-2))+2 • (6 • 2-(-3) • (-2)) = 10

Заменим 3-ый столбец матрицы А на вектор результата В.

-3	1	6
2	-1	-3
2	3	5

Найдем определитель полученной матрицы. ∆₃ = (-1)^{1 + 1}a₁₁∆₁₁ + (-1)^{2 + 1}a₂₁∆₂₁ + (-1)^{3 + 1}a₃₁∆₃₁ = (-3) • ((-1) • 5-3 • (-3))-2 • (1 • 5-3 • 6)+2 • (1 • (-3)-(-1) • 6) = 20

Выпишем отдельно найденные переменные Х

Метод Гаусса

Запишем систему в виде расширенной матрицы:

-3 1 -2 2 -1 2 2 3 4

6 -3 5

Умножим 1-ую строку на (2). Умножим 2-ую строку на (3). Добавим 2-ую строку к 1-ой:

0 -1 2 2 -1 2 2 3 4

3 -3 5

Умножим 3-ую строку на (-1). Добавим 3-ую строку к 2-ой:

0 -1 2 0 -4 -2 2 3 4

3 -8 5

Умножим 1-ую строку на (4). Умножим 2-ую строку на (-1). Добавим 2-ую строку к 1-ой:

0 0 10 0 -4 -2 2 3 4

20 -8 5

Теперь исходную систему можно записать так:

Задача 10

Для заданной системы линейных уравнений проверьте выполнение условий теоремы Кронекера-Капелли. Если система совместна, то найдите её общее решение, укажите размерность и базис пространства решений.

Решение

Исследуем эту систему по теореме Кронекера-Капелли. Выпишем расширенную и основную матрицы:

2	1	-1	-1	1	1
1	-1	1	1	-2	0
3	3	-3	-3	4	2
4	5	-5	-5	7	3

Здесь матрица А выделена жирным шрифтом. Приведем матрицу к треугольному виду. Будем работать только со строками, так как умножение строки матрицы на число, отличное от нуля, и прибавление к другой строке для системы означает умножение уравнения на это же число и сложение с другим уравнением, что не меняет решения системы.

Умножим 1-ую строку на (-1). Умножим 2-ую строку на (2). Добавим 2-ую строку к 1-ой:

0	-3	3	3	-5	-1
1	-1	1	1	-2	0
3	3	-3	-3	4	2
4	5	-5	-5	7	3

Умножим 2-ую строку на (-3). Добавим 3-ую строку к 2-ой:

0	-3	3	3	-5	-1
0	6	-6	-6	10	2
3	3	-3	-3	4	2
4	5	-5	-5	7	3

Умножим 3-ую строку на (-4). Умножим 4-ую строку на (3). Добавим 4-ую строку к 3-ой:

0	-3	3	3	-5	-1
0	6	-6	-6	10	2
0	3	-3	-3	5	1
4	5	-5	-5	7	3

Умножим 1-ую строку на (2). Добавим 2-ую строку к 1-ой:

0	0	0	0	0	0
0	6	-6	-6	10	2
0	3	-3	-3	5	1
4	5	-5	-5	7	3

В матрице B 1-ая строка нулевая, следовательно, вычеркиваем ее. Это равносильно вычеркиванию 1-го уравнения системы.

0	6	-6	-6	10	2
0	3	-3	-3	5	1
4	5	-5	-5	7	3

Умножим 1-ую строку на (-1). Умножим 2-ую строку на (2). Добавим 2-ую строку к 1-ой:

0	0	0	0	0	0
0	3	-3	-3	5	1
4	5	-5	-5	7	3

В матрице B 1-ая строка нулевая, следовательно, вычеркиваем ее. Это равносильно вычеркиванию 1-го уравнения системы.

0	3	-3	-3	5	1
4	5	-5	-5	7	3

Определим ранг системы.

0	3	-3	-3	5
4	5	-5	-5	7

Выделенный минор имеет наивысший порядок (из возможных миноров) и отличен от нуля (он равен произведению элементов, стоящих на обратной диагонали), причем этот минор принадлежит как основной матрице, так и расширенной, следовательно, rang(A) = rang(B) = 2. Поскольку ранг основной матрицы равен рангу расширенной, то система является совместной. Этот минор является базисным. В него вошли коэффициенты при неизвестных x₁,x₂, значит, неизвестные x₁,x₂ – зависимые (базисные), а x₃,x₄,x₅ – свободные.

Преобразуем матрицу, оставляя слева только базисный минор.

0	3	1	3	3	-5
4	5	3	5	5	-7
x1	x2		x3	x4	x5

Система с коэффициентами этой матрицы эквивалентна исходной системе и имеет вид:

3x₂ = 1 + 3x₃ + 3x₄ - 5x₅

4x₁ + 5x₂ = 3 + 5x₃ + 5x₄ - 7x₅

Методом исключения неизвестных находим:

Получили соотношения, выражающие зависимые переменные x₁,x₂ через свободные x₃,x₄,x₅, то есть нашли общее решение:

x₂ = ¹/₃ + x₃ + x₄ - ⁵/₃x₅

x₁ = ¹/₃ + ¹/₃x₅ Придавая свободным неизвестным любые значения, получим сколько угодно частных решений. Система является неопределенной, т.к. имеет более одного решения.