15. Машины Поста. Функции, вычислимые по Посту

В машине Поста имеется лента, разбитая на ячейки, и бесконечная в обе стороны, а также каретка, способная считывать символ с обозреваемой ячейки, заменять этот символ и двигаться вдоль ленты на одну ячейку вправо или влево. Каждая ячейка ленты либо пустая, либо содержит символ 1. Мы считаем, что пустая ячейка содержит символ 0. Записывать символ 0 – это значит стереть с ячейки символ 1. Программа состоит из пронумерованных команд. Команды рассматриваем следующих пяти видов:

 i (переместить каретку вправо и перейти к команде с номером i);

 i (переместить каретку влево и перейти к команде с номером i);

0i (записать в обозреваемую ячейку 0 и перейти к команде с номером i);

1i (записать в обозреваемую ячейку 1 и перейти к команде с номером i);

?i,n (если текущая ячейка содержит 0, то перейти к команде с номером i, иначе перейти к команде n;

. (остановить программу).

Номер команды перехода в командах , , 0 и 1 можно не указывать, при этом происходит переход к следующей команде.

Работа начинается с выполнения команды с номером 1, останавливается с результатом для команды с точкой и без результата для невыполнимой команды.

Представим натуральное число как слово, состоящее из единиц: . Числовая -местная функция называется вычислимой по Посту, если существует машина Поста, которая слово на ленте преобразует в слово , если функция определена и равна , и останавливается без результата или не останавливается, если функция не определена.

Пример 1. Программа Поста для вычисления функции сигнума sg(x):

1		5	? 6,7
2	? 3,4	6	.
3	.	7	0,4
4	

Пример 2. Программа Поста для вычисления сложения xy:

1	? 3,2	6	
2	 1	7	0
3	1	8	
4	? 6,5	9	0
5	 4	10	.

16. Нумерация множества упорядоченных пар натуральных чисел

Нумерация Кантора упорядоченных пар натуральных чисел.

Декартово произведение – множество всех упорядоченных пар натуральных чисел является не только счетным, но эффективно счетным множеством. Это значит: существует биекция , такая, что функции и вычислимые. Биекция (или ) называется нумерацией, или перечислением, множества , если функции и вычислимые.

Из всех возможных нумераций множества мы рассмотрим нумерацию Кантора, а именно построим функции , и , такие, что, если и , то , докажем, что функции , , – примитивно рекурсивные. Обратная функция не является числовой функцией (ее значениями являются не числа, а упорядоченные пары), но, поскольку и примитивно рекурсивны, то эта функция будет вычислимой с точки зрения интуитивного определения алгоритма.

Нумерация Кантора, т.е. нахождение номера пары , где , происходит следующим образом:

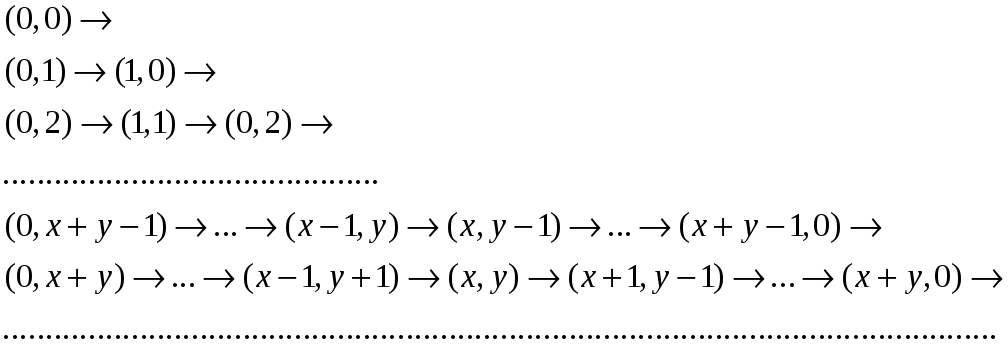
Строка, начинающаяся с пары , содержит пар. Первые строк содержат пар.

Следовательно, , и  ПРФ.

Чтобы показать, что соответствия и являются функциями, причем, примитивно рекурсивными, мы обозначим: . Тогда из равенства следует, что и .

Легко увидеть, что  это наибольшее число , что . Чтобы применить -оператор, мы рассмотрим  это наименьшее число , что . Тогда . Теперь последовательно построим следующие ПРФ: ; ; ; .

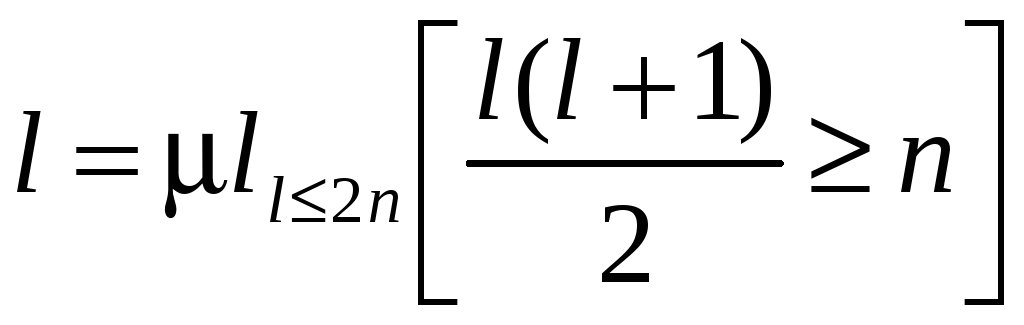Мы доказали, что существуют такие (примитивно рекурсивные) функции , и , что для всех .

Покажем, что  биекция. Пусть . Тогда по определению понятия функции получим, что и .

Сформулируем теперь доказанное утверждение в виде теоремы.

Теорема. Существуют примитивно рекурсивные биекция и функции и , такие, что для всех .

Примечание. Записи и не являются доказательствами примитивной рекурсивности функций и , так как функция не является примитивно рекурсивной (даже, числовой) функцией.