
- •При ряд сходится,
- •При ряд расходится (не выполнено необходимое условие сходимости),
- •В случае требуются дополнительные исследования.
- •1.Я.С.Бугров, c.М. Никольский. Высшая математика: - т.2. Дифференциальное и интегральное исчисление. М., Наука (Дрофа). 2007.
- •1.Я.С.Бугров, c.М. Никольский. Высшая математика: - т.2. Дифференциальное и интегральное исчисление. М., Наука (Дрофа). 2007.
- •1.Я.С.Бугров, c.М. Никольский. Высшая математика: - т.2. Дифференциальное и интегральное исчисление. М., Наука (Дрофа). 2007.
Модуль 7
«Ряды»
дисциплины
«Математический анализ»
Содержание лекционного материала
Лекция 37. Числовые ряды. Сходимость. Свойства сходящихся рядов. Признаки сравнения.
Основные понятия: числовой ряд, сумма ряда, сходимость ряда.
-
Основные понятия.
Суммы
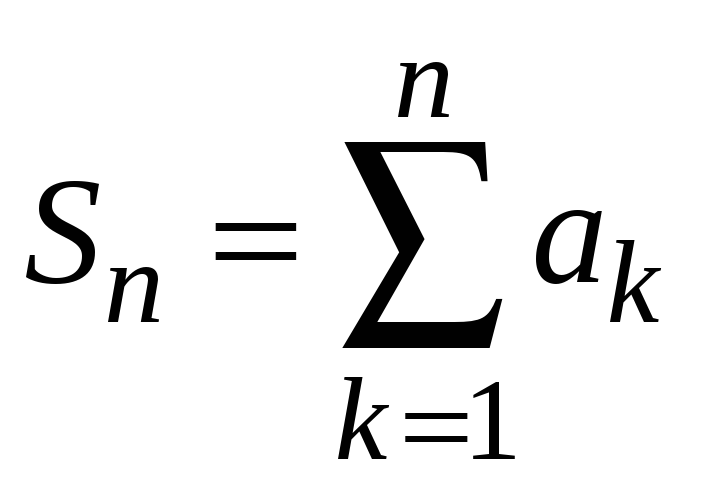 называются частичными суммами ряда
называются частичными суммами ряда
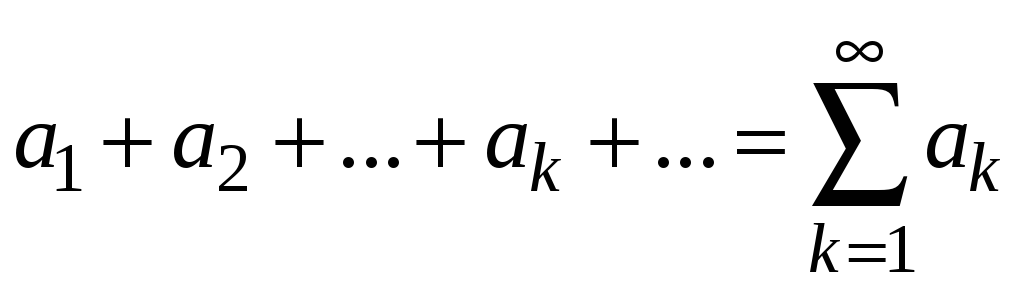 ,
,
где
![]() – действительные или комплексные числа.
– действительные или комплексные числа.
Числовой
ряд называется сходящимся, если сходится
последовательность его частичных сумм
![]() .
Предел последовательности частичных
сумм называется суммой ряда
.
Предел последовательности частичных
сумм называется суммой ряда
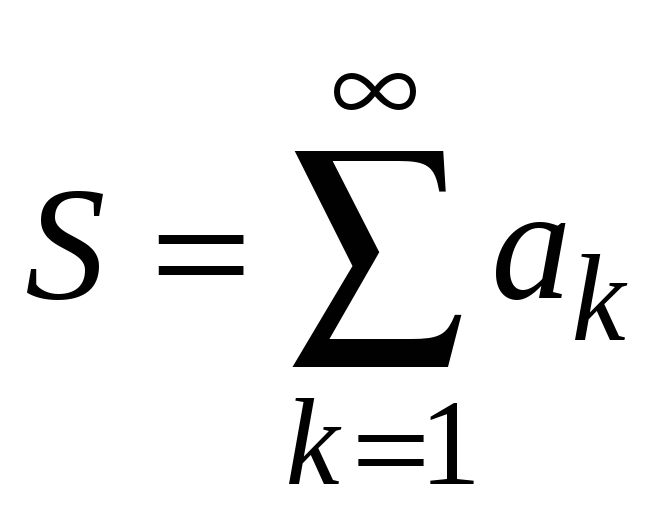 .
.
-
Необходимое условие сходимости ряда
Если
![]() сходится, то
сходится, то
![]() .
.
-
Признаки сравнения.
Пусть
![]() .
Тогда:
.
Тогда:
-
если ряд
 сходится, то сходится и ряд
сходится, то сходится и ряд
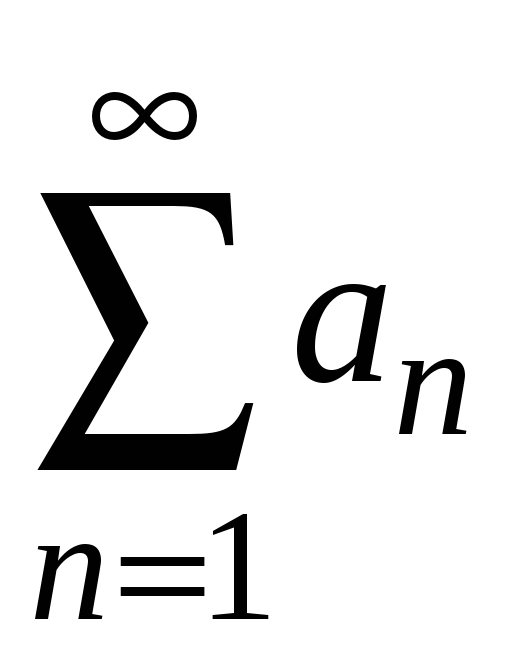 ;
;
-
если расходится ряд
 ,
то расходится и ряд
,
то расходится и ряд
 .
. -
(предельный признак сравнения)
пусть
![]() ,
,
![]() и
и![]() ,
,
![]() .
Тогда ряды
.
Тогда ряды
![]() и
и
![]() сходятся или расходятся одновременно.
сходятся или расходятся одновременно.
Литература к лекции 37
1.Я.С.Бугров, C.М. Никольский. Высшая математика: - Т.2. Дифференциальное и интегральное исчисление. М., Наука (Дрофа). 2007.
Лекция 38. Признаки Даламбера, Коши. Интегральный признак Коши. Признак Лейбница.
Основные понятия: числовой ряд, сходимость, знакочередующийся ряд, абсолютная сходимость, условная сходимость.
План лекции.
-
Признаки Даламбера, Коши.
Признак
Даламбера.
Пусть
![]() -
ряд с положительными членами
-
ряд с положительными членами
![]() >0
и
>0
и
![]() ,
тогда
,
тогда
-
При ряд сходится,
-
При ряд расходится (не выполнено необходимое условие сходимости),
-
В случае требуются дополнительные исследования.
Признак
Коши (радикальный).
Пусть
![]() — ряд с неотрицательными членами
— ряд с неотрицательными членами
![]() и
и
![]() ,
тогда
,
тогда
1)
в случае
![]() ряд
ряд
![]() сходится,
сходится,
2)
в случае
![]() ряд
ряд
![]() расходится
(не выполнено необходимое условие
сходимости),
расходится
(не выполнено необходимое условие
сходимости),
3)
в случае
![]() требуются дополнительные исследования.
требуются дополнительные исследования.
-
Интегральный признак Коши.
Если
функция
![]() и
и
![]() (монотонно убывает) при всех
(монотонно убывает) при всех
![]() ,
то ряд
,
то ряд
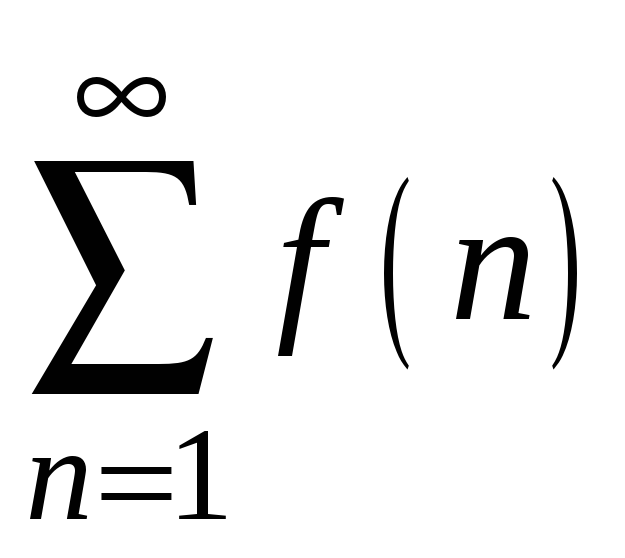 сходится тогда и только тогда, когда
сходится несобственный интеграл
сходится тогда и только тогда, когда
сходится несобственный интеграл
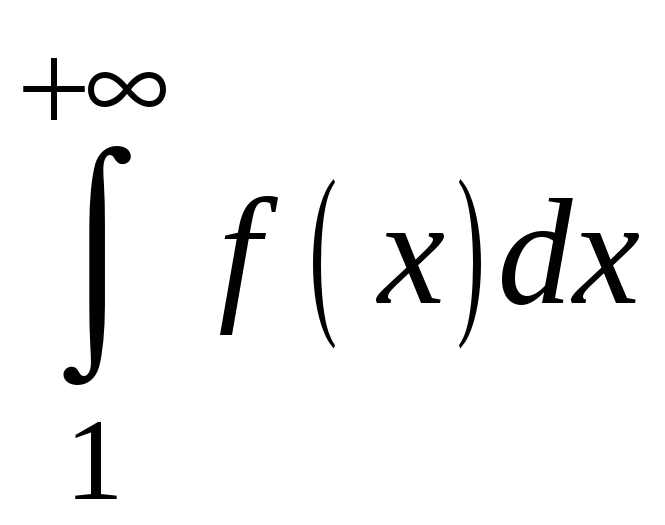 .
.
-
Условия сходимости рядов Дирихле.
-
Знакочередующиеся ряды. Признак Лейбница.
Теорема
Лейбница. Если
![]() и
и
![]() для всех
для всех
![]() ,
то знакочередующийся ряд
,
то знакочередующийся ряд

сходится
и его сумма
![]() .
.
Следствие.
Для
всех
![]()
![]() - модуль
- модуль
![]() -ого
остатка ряда не превышает модуля
следующего члена ряда.
-ого
остатка ряда не превышает модуля
следующего члена ряда.
-
Абсолютная сходимость. Условная сходимость.
Если
ряд из модулей
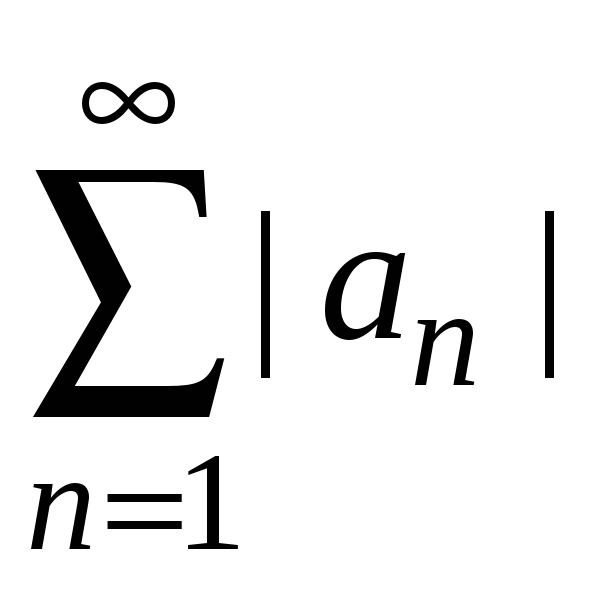 сходится, то исходный ряд
сходится, то исходный ряд
![]() называется абсолютно сходящимся.
называется абсолютно сходящимся.
Для
исследования абсолютной сходимости
используют признаки сходимости рядов
с положительными членами, применяемых
к ряду
![]() .
.
Если
ряд
![]() сходится, а ряд из модулей
сходится, а ряд из модулей
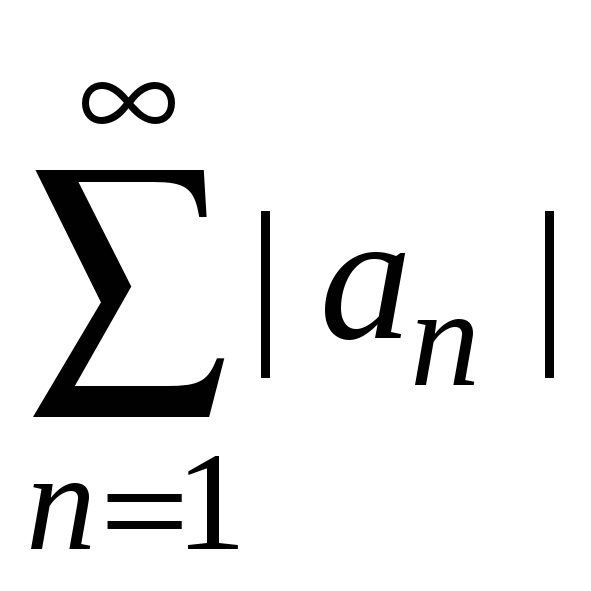 расходится, то исходный ряд
расходится, то исходный ряд
![]() называется условно сходящимся.
называется условно сходящимся.
Признак
Абеля-Дирихле.
Пусть дан ряд
 ,
в котором последовательность
,
в котором последовательность
![]() монотонно стремится к
монотонно стремится к
![]() ,
а последовательность частичных сумм
,
а последовательность частичных сумм
![]() ряда
ряда
![]() равномерно ограничена, тогда ряд
равномерно ограничена, тогда ряд
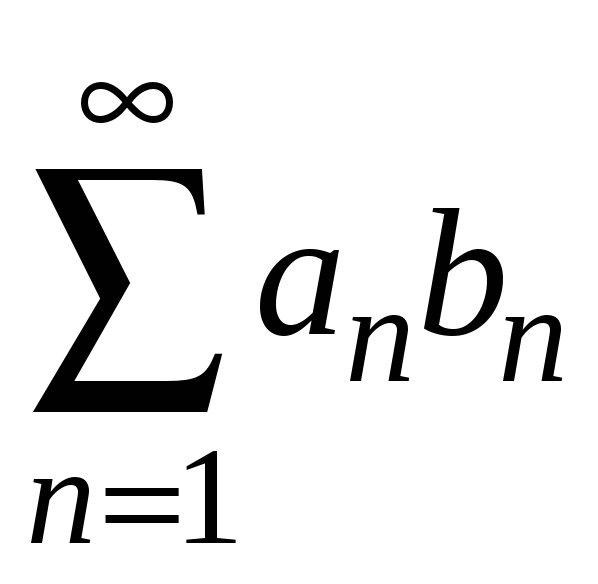 - сходится.
- сходится.
Литература к лекции 38
1.Я.С.Бугров, c.М. Никольский. Высшая математика: - т.2. Дифференциальное и интегральное исчисление. М., Наука (Дрофа). 2007.
Лекция 39. Степенной ряд. Теорема Абеля.
Основные понятия: степенной ряд, область сходимости, радиус сходимости.
-
Сходящийся в области
 функциональный ряд
функциональный ряд
 называется равномерно
сходящимся
в этой области, если для любого
называется равномерно
сходящимся
в этой области, если для любого
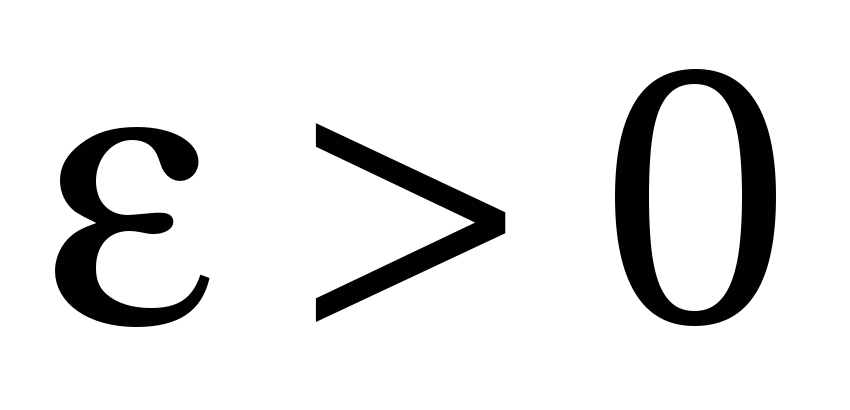 найдется число
найдется число
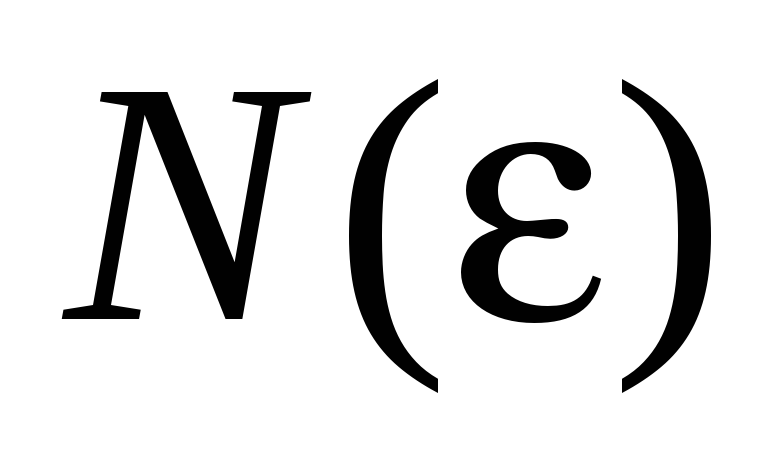 такое, что для остатка функционального
ряда
такое, что для остатка функционального
ряда
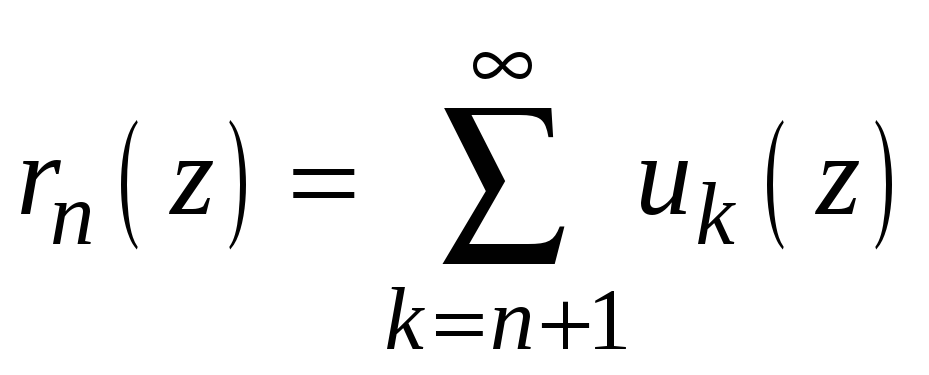 при всех
при всех
 и
и
 одновременно имеет место оценка
одновременно имеет место оценка
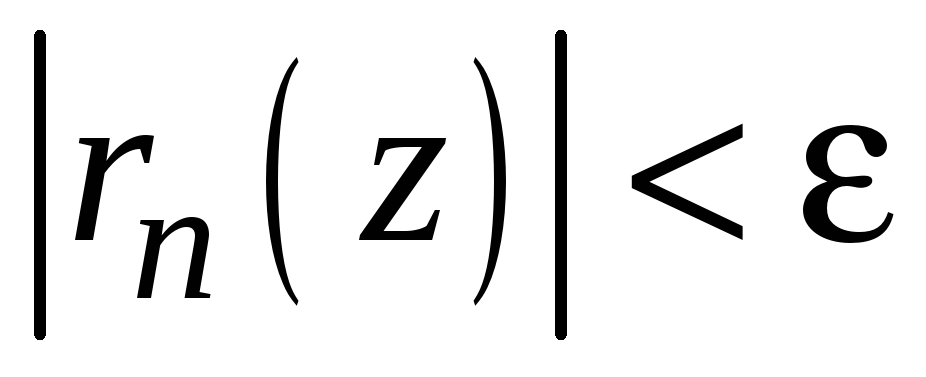 .
.
-
Признак Вейерштрасса. Пусть функциональный ряд
 сходится области
сходится области
 и пусть существует сходящийся
знакоположительный числовой ряд
и пусть существует сходящийся
знакоположительный числовой ряд
 такой, что для всех
такой, что для всех
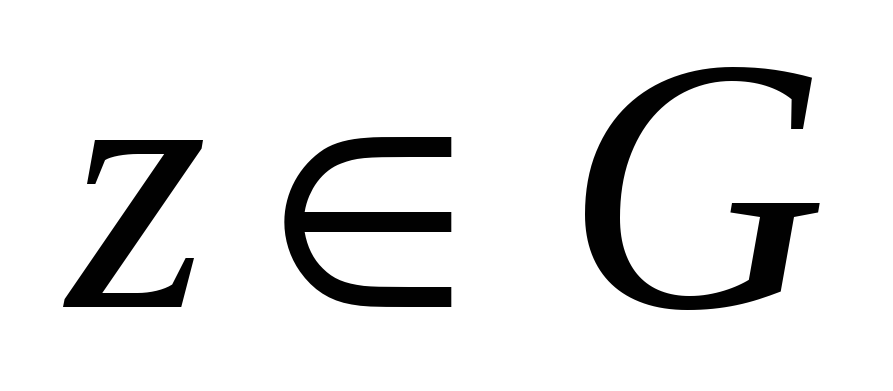 и для всех
и для всех
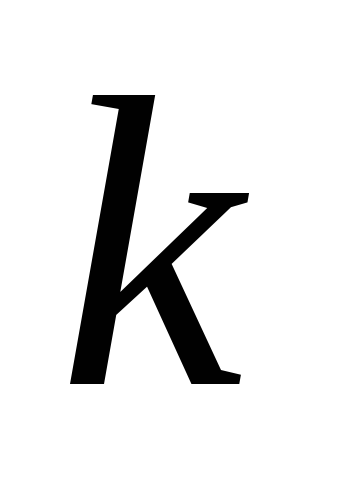 ,
начиная с некоторого номера, члены ряда
,
начиная с некоторого номера, члены ряда
 удовлетворяют условию
удовлетворяют условию
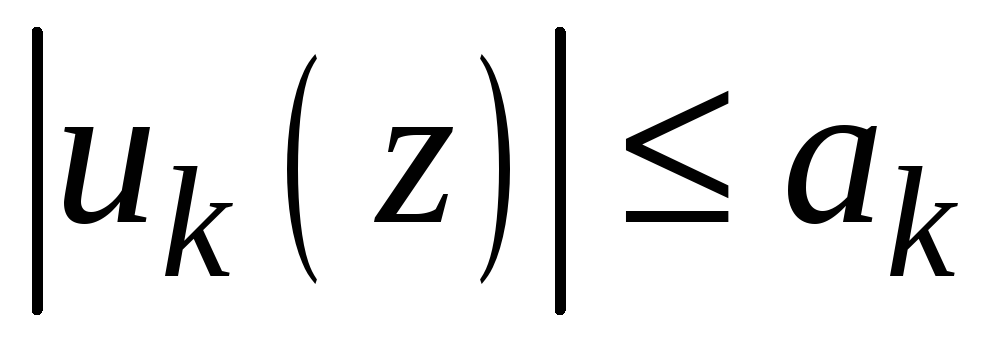 .
Тогда ряд
.
Тогда ряд
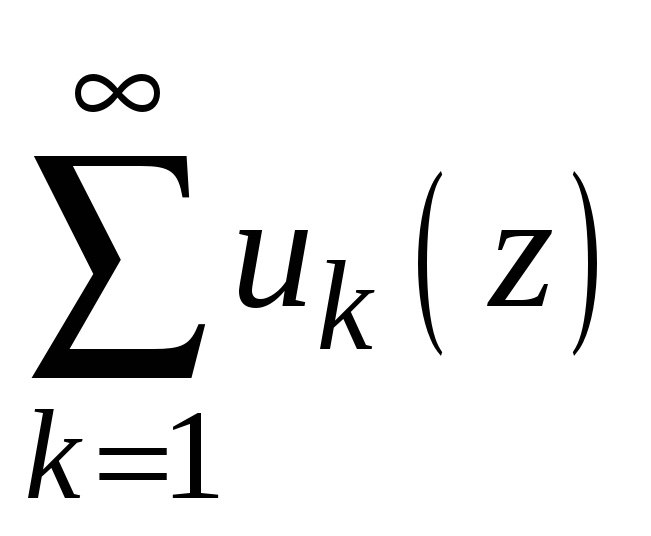 сходится абсолютно и равномерно в
области
сходится абсолютно и равномерно в
области
 .
. -
Теорема Абеля. Если степенной ряд
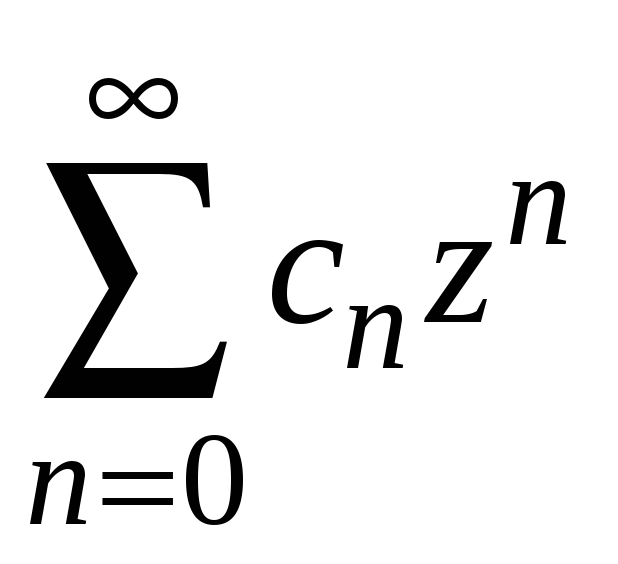 сходится в точке
сходится в точке
 ,
то он абсолютно сходится для всех
,
то он абсолютно сходится для всех
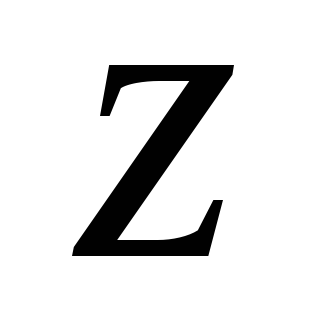 ,
таких, что
,
таких, что
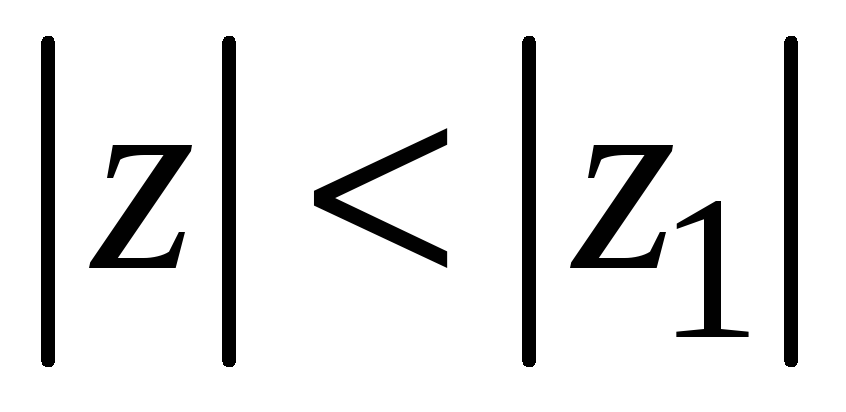 ,
причем сходимость будет равномерной
в любом замкнутом круге
,
причем сходимость будет равномерной
в любом замкнутом круге
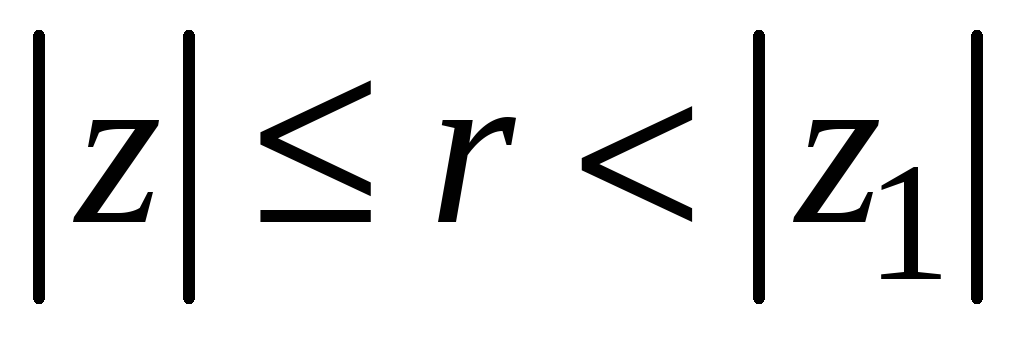 .
Если же ряд
.
Если же ряд
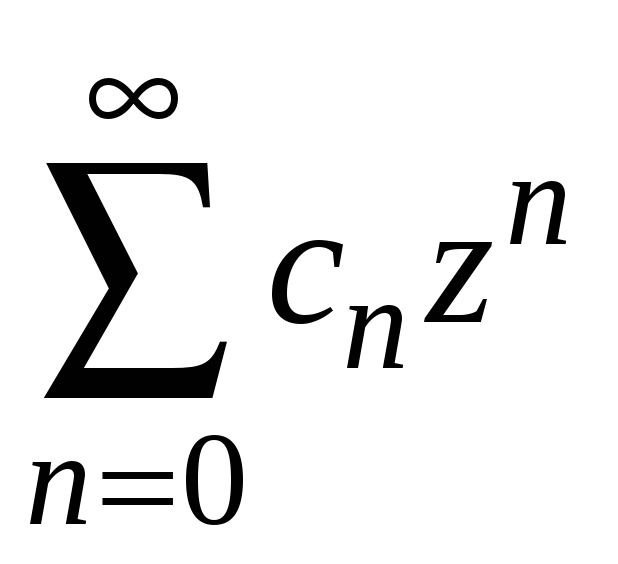 расходится в точке
расходится в точке
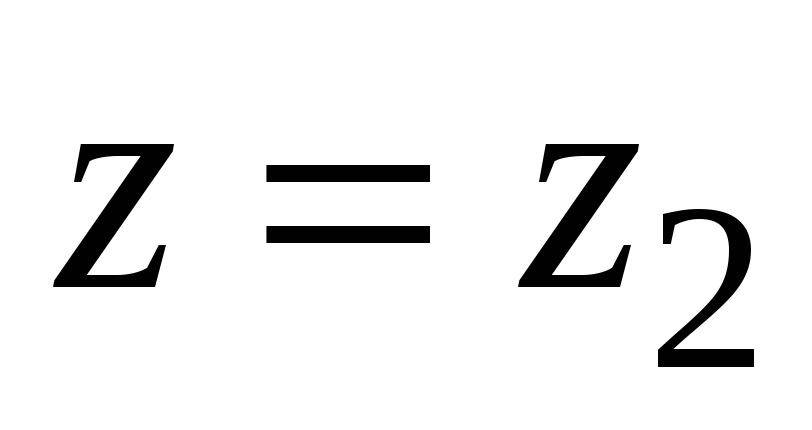 ,
то он расходится и для всех
,
то он расходится и для всех
 таких, что
таких, что
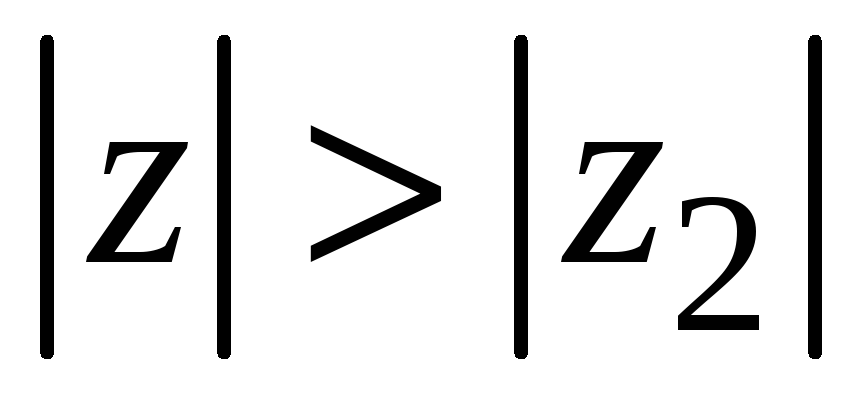 .
.
Замечание.
а) Из теоремы Абеля следует существование
круга сходимости. б) Из признака
Вейерштрасса следует: если степенной
ряд
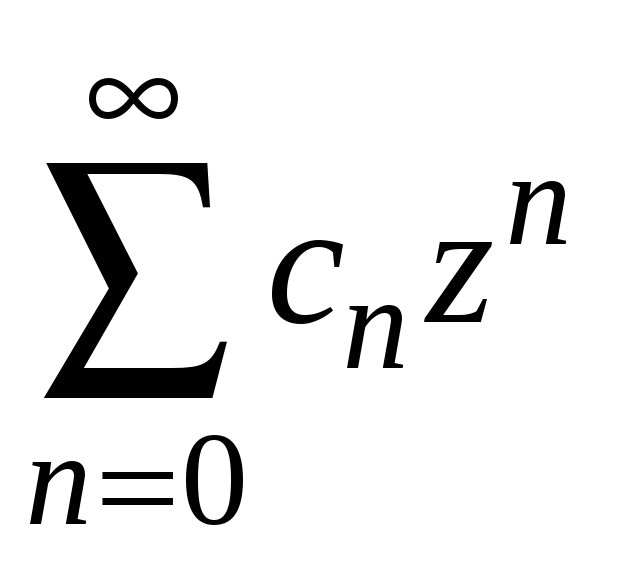 абсолютно сходится и на границе круга
сходимости, то сходимость равномерная
внутри всего замкнутого круга сходимости.
абсолютно сходится и на границе круга
сходимости, то сходимость равномерная
внутри всего замкнутого круга сходимости.
Литература к лекции 39.
1.Я.С.Бугров, c.М. Никольский. Высшая математика: - т.2. Дифференциальное и интегральное исчисление. М., Наука (Дрофа). 2007.
Лекция 40. Ряд Тейлора.
Основные понятия: ряд Тейлора, ряд Маклорена.
-
Понятие ряда Тейлора.
-
Разложение элементарных функций (ex, cosx, sinx, ln(1 + x), arctgx, (1 + x)). Разложения основных элементарных функций:
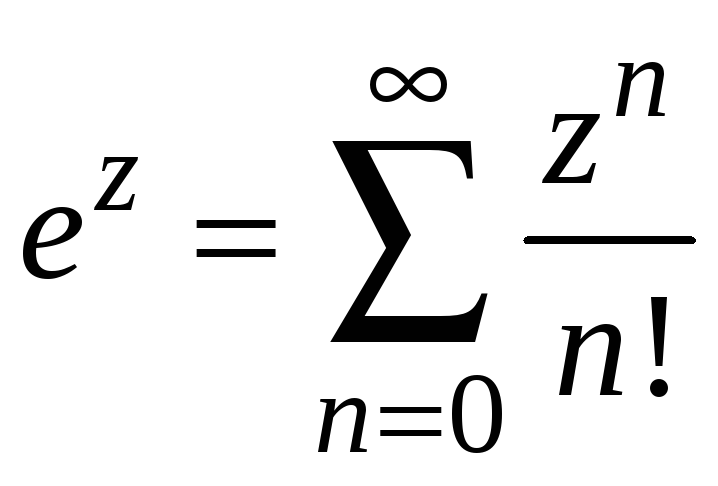 ,
,
![]() ;
;
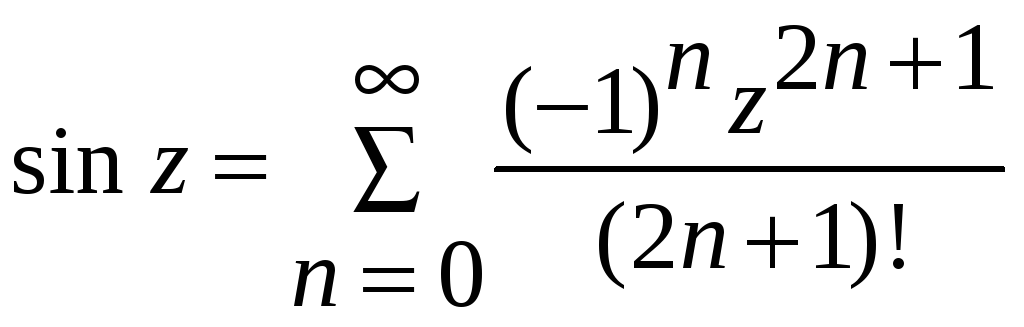 ,
,
![]() ;
;
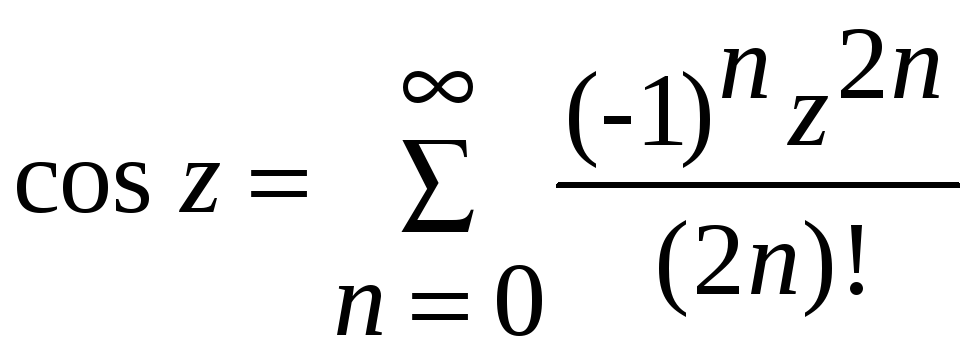 ,
,
![]() ;
;
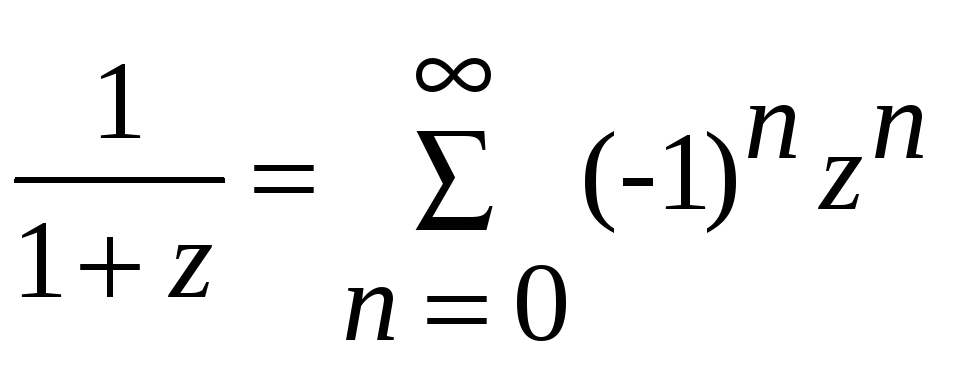 ,
,
![]() ;
;
 ,
,
![]() ;
;
 ,
,
![]() .
.
-
Применение ряда Тейлора в приближенных вычислениях.
Литература к лекции 40.
