52. Оператор поворота вектора

Большинство электрических машин переменного тока предназначено для работы в трехфазных сетях, поэтому они строятся с симметричными трехфазными обмотками на статоре, причем МДС этих обмоток распределены в пространстве по закону близкому к синусоидальному, т.е. МДС, создаваемая k-й обмоткой в точке, отстоящей от оси этой обмотке на угол a _k равна –Fa _k=F_k0cosa _k, где F_k0 – МДС, соответствующая оси k-й обмотки. Синусоидальность распределения позволяет представить МДС или пропорциональные им токи обобщенным пространственным вектором на комплексной плоскости, т.е. вектором, представляющим собой геометрическую сумму отрезков, построенных на пространственных осях фазных обмоток и соответствующих мгновенным значениям фазных МДС или токов. При этом проекции обобщенного вектора на оси фазных обмоток в любой момент времени будут соответствовать мгновенным значениям соответствующих величин.

При симметричной трехфазной системе обмоток обобщенный вектор тока можно представить в виде

(1.1.1)

где – операторы поворота, аi_a, i_b и i_c – мгновенные значения токов соответствующих обмоток.

Оператор поворота вектора 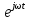– множитель вектора, означающий поворот этого вектора на угол . Обозначение вектора строчным символом принято для указания на то, что его координаты являются функциями времени аналогично тому, как строчные символы при обозначении скалярных величин указывают на мгновенное значение.

При таком представлении фазные токи i_a, i_b и i_c можно рассматривать как проекции вектора i на соответствующие оси фазных обмоток (рис. 1.1 а)). Если произвести построение вектора i , откладывая значения фазных токов i_a, i_b и i_c на осях обмоток (рис. 1.1 б)), то суммарный вектор окажется в полтора раза больше того вектора, проекции которого соответствуют фазным токам. Поэтому в выражении (1.1.1)присутствует коэффициент 2/3, приводящий модуль суммарного вектора к такому значению, которое при проецировании на оси фазных обмоток даст истинные значения фазных токов.

Если статор машины имеет нулевой провод, то фазные токи могут содержать нулевую составляющую и их значения можно представить в виде i_a+i_o, i_b+i_o и i_c+i_o. Тогда вектор тока будет равен

Таким образом, обобщенный вектор тока статора не содержит нулевой составляющей и ее при анализе следует учитывать особо.

53.Разложение 3-х фазного не синусоидального тока на вектора прямой, обратной и нулевой последовательности.

В эксплуатации отдельные фазы трансформатора могут быть нагружены несимметрично из-за неравномерного распределения по фазам осветительной или другой однофазной нагрузки. Иногда имеются и несимметричные режимы, вызванные авариями — одно- и двухфазными короткими замыканиями в электрических сетях, питающихся от трансформаторов.

При несимметричных нагрузках ЭДС вторичных обмоток (а следовательно, и напряжения) могут существенно отличаться от их значений при нормальных, симметричных режимах, а это отрицательно влияет на работу потребителей электрической энергии, особенно на лампы накаливания и на асинхронные двигатели.

Общий метод анализа несимметричных режимов. При анали­зе будем считать заданными:

1) первичные линейные напряжения, векторы которых обра­зуют симметричную трехлучевую звезду (мощность питающей сети предполагается очень большой);

2) векторы вторичных токов, определяемые значением и ха­рактером нагрузки.

Общим методом анализа несимметричных режимов явля­ется метод симметричных составляющих, согласно которому трехфазная несимметричная система токов 1а, 1b и 1c (рис. 2.69, а) разлагается на системы токов прямой, обратной и нулевой последовательностей, т. е. производится замена:

Ía = Ía1 + Ía2 + Ía0 Íb = Íb1 + Íb2 + Íb0 Íc = Íc1 + Íc2 + Íc0

}

(2.105)

Векторы Í_а1 Í_b1 и Í_c1 создают систему векторов прямой последовательности (рис. 2.69,6), т. е. имеют то же чередование фаз, что и заданная система векторов Í_а, Í_b и Í_c. Следовательно, Í_b1 = e^j4π/3Í_а1; Í_c1 =e ^j2π/3Í_а1. Система векторов обратной последовательности

Рис. 2.69. Разложение несимметричной системы токов (а) на симметричные составляющие (б, в, г)

Í_а2, Í_b2 и Í_с2 (рис. 2.69, в) имеет обратное чередование фаз и характеризуется соотношениями Í_b2 = e^j2π/3Í_а2 и Í_с2 = e^j4π/3Í_а2. Напомним, что умножение вектора на е^jφсоответствует повороту вектора в сторону, противоположную вращению часовой стрелки.

Система векторов нулевой последовательности показана на рис. 2.69,г. Для нее характерно соотношение I_a0 =I_b0= I_c0.

Подставляя значения указанных векторов в (2.105) и учитывая, что сумма 1 + e ^j2π/3+ e ^j4π/3 = 0, можно найти значения векторов:

Ía1 = (⅓)(Ía + ej2π/3Íb+ ej4π/3Íc); Ía2 = (⅓)(Ía + ej4π/3Íb+ ej2π/3Íc); Ía0 = (⅓)(Ía + Íb + Íc).

}

(2.106)