Московский технический университет связи и информатики

Курсовая работа по вычислительной математике

Кафедра вычислительной математики и программирования

Работу выполнил:

Студент ОТФ-2

группы БСТ1401

Петров Сергей, вариант 18

Работу проверила:

Семёнова Т.И.

Москва 2015

1. Задание на курсовую работу

Получить таблицу значений дифференциального уравнения

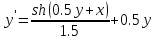
где y(0) = 0 для x ∈[a,b] с шагом h.

Построить интерполяционный многочлен 2-ой степени по полученной таблице решений.

Исходные данные:

a	b	h	E
0	1	0.5	10-3

Метод решения дифференциального уравнения: рунге-кутта 2-ого порядка.

Метод вычисления интерполяционного многочлена: метод ньютона.

Код программы

1.Метод рунге-кутта

#include <iostream>

#include <locale.h>

#include <cmath>

#include <conio.h>

#include <stdio.h>

using namespace std;

double F(double x, double y)

{

return sinh(y / 2 + x + y / 2) / 1.5;

}

int main()

{

double y, z, a, b, h;

setlocale(LC_ALL, "rus");

cout << endl << " Введите значение y0: ";

cin >> y;

cout << endl << " Введите значение a ";

cin >> a;

cout << endl << " Введите значение b ";

cin >> b;

cout << endl << " Введите значение h: ";

cin >> h;

for (double i = a; i <= b; i += h)

{

cout << endl << "x=" << i << endl;

cout << "y=" << y << endl << endl;

z = y + (h*y*(1 - i));

y += h*(F(i,z)+F(i+h,z)) / 2;

}

return 0;

}

2.Метод ньютона

#include<iostream>

#include<conio.h>

#include<math.h>

using namespace std;

double* vvod(int num)

{

double* n = new double[num];

for (int i = 0; i <= num; i++)

cin >> n[i];

return n;

}

void vivod(double* n, int num)

{

for (int i = 0; i <= num; i++)

cout << n[i] << " ";

}

int factorial(int n)

{

int num = 1;

for (int i = 1; i <= n; i++)

num = num * i;

return num;

}

double* dy(double* y, int n)

{

double* dy = new double[n - 1];

for (int i = 0; i <= n; i++)

dy[i] = y[i + 1] - y[i];

return dy;

}

void reshenie(double* x, double* y, double a, int n, double& P)

{

double S = 1;

double h = x[1] - x[0];

double* razn1 = dy(y, n);

double* razn2 = dy(razn1, n - 1);

double* razn3 = dy(razn2, n - 2);

double razn[] = { razn1[0], razn2[0], razn3[0] };

P = y[0];

for (int i = 0; i <= 2; i++)

{

S = S * (a - x[i]);

P = P + razn[i] / (factorial(i + 1)*pow(h, i + 1))*S;

}

}

void main()

{

setlocale(LC_ALL, "rus");

double a, P, R;

int n = 2;

int m;

cout << "Введите значения x:\n";

double* x = vvod(n);

cout << "Введите значения y:\n";

double* y = vvod(n);

cout << "Введите значениe a:\n";

cin >> a;

cout << "Введите степень полинома:\n";

cin >> m;

reshenie(x, y, a, n,P);

cout << "Значение интерполирующего полинома: ";

cout << P << endl;

_getch();

}