Прямая линия в пространстве.

Примеры:

Задача № 1. Найти уравнение прямой, проходящей через точку К(-3;4;-5) параллельно прямой

Решение:

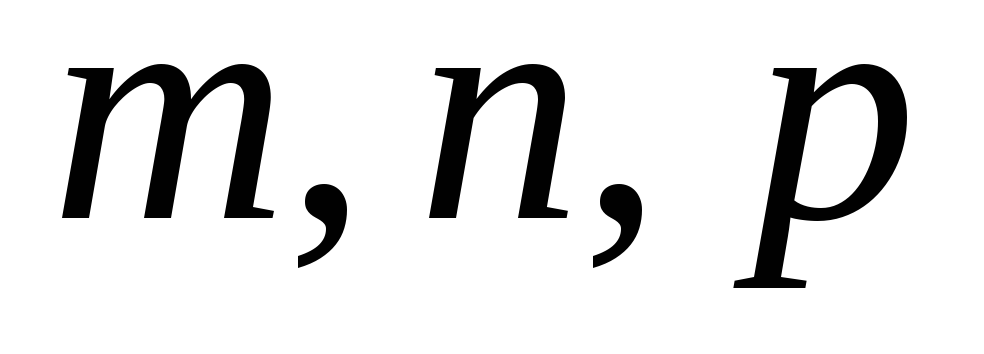1. Найдем координаты направляющего вектора прямой - это каноническое уравнение прямой в пространстве. Каноническое уравнение прямой в пространстве задается формулой , где -текущие координаты; - координаты заданной точки, через которую проходит прямая; - координаты направляющего вектора прямойS.

Сравнивая уравнения и находим, что - координаты направляющего вектора данной прямой, т. е.

2. Так как прямая параллельна данной прямой, то направляющие векторы коллинеарны. Если векторы коллинеарны, то соответствующие координаты векторов пропорциональны. Поэтому, обозначив координаты направляющего вектора искомой прямой через , получим, что где коэффициент пропорциональности.

3. Каноническое уравнение искомой прямой будем искать по формуле:

Подставив в эту формулу x y координаты точки К(-3;4;-5), а вместо координаты направляющего вектора этой прямой () получим: . Сократив на , получим:

- каноническое уравнение искомой прямой.

Ответ: .

Решить самостоятельно:

Задача № 2. Найти уравнение прямой, проходящей через точку К(2;-1;7) параллельно прямой

Ответ:

Задача № 3. Найти уравнение прямой, проходящей через точку К(0;2;-5) параллельно прямой

Ответ:

Практическое занятие № 8 на тему:

Плоскость в пространстве

Примеры:

Задача № 1. Найти уравнение прямой, проходящей через точку К(0;-3;4) параллельной плоскости .

Решение:

1. Найдем координаты нормального вектора плоскости . - это общее уравнение плоскости. Общее уравнение плоскости задается формулой: , где x, y, z- текущие координаты. Сравнивая уравнения и , найдем, что А=1;

В=3; С=2 - координаты нормального вектора данной плоскости, т. е.

2. Так как искомая плоскость параллельна данной плоскости, то нормальные векторы этих плоскостей коллинеарны, У коллинеарных векторов соответствующие координаты пропорциональны. Обозначив координаты нормального вектора искомой плоскости: , получим, что где коэффициент пропорциональности.

3. Уравнение искомой плоскости будем искать по формуле

, где -текущие координаты; - координаты известной точки, через которую проходит плоскость; - координаты нормального вектора плоскости. Подставив в эту формулу вместо координаты точки К(0;-3;4), вместо координаты нормального вектора этой плоскости получим: сократив на и раскрыв скобки, получим:

- общее уравнение искомой плоскости.

Ответ:

Решить самостоятельно:

Задача № 1. Найти уравнение прямой, проходящей через точку К(3;4;-2) параллельной прямой .

Ответ:

Задача № 2. Найти уравнение прямой, проходящей через точку К(-1;0;-5) параллельной прямой

Ответ:

Практическое занятие № 9 на тему:

ПРЯМАЯ И ПЛОСКОСТЬ В ПРОСТРАНСТВЕ.

Примеры:

Задача № 1. Найти уравнение прямой, проходящей через точку (3;0;-2) перпендикулярно плоскости

Решение:

1. - это общее уравнение плоскости, которое задается формулой . Сравнивая эти уравнения, найдем координаты нормального вектора плоскости: А=3; В=4; С=-2; .

2. Так как прямая перпендикулярна плоскости, то направляющий вектор и нормальный вектор плоскости коллинеарны. Если векторы коллинеарны пропорциональны, т.е. , где , - нормальный вектор плоскости, - направляющий вектор прямой. Подставив А=3, В=4, С=-2, получим . Обозначим , Тогда ,,,

3. Для нахождения уравнения прямой воспользуемся формулой

, где в нашем случае

. Тогда уравнение примет вид:

Сократив на получим

Ответ:

Задача № 2. Найти уравнение плоскости, проходящей через точку К(1;2;-1) перпендикуляр прямой

Решение:

1. - это канонические уравнения прямой в пространстве, которые задаются формулой

Сравнив эти два уравнения, найдем - координаты направляющего вектора прямой, т.е.

2. Так как прямая и плоскость перпендикулярны, то координаты направляющего вектора пропорциональны соответствующим координатам нормального вектора плоскости:

Обозначив коэффициент пропорциональности через , получим =

3. Для нахождения уравнения плоскости воспользуемся формулой

, где в нашем случае:

.

В результате подстановки получим: .Сократим на .

Ответ:

Решить самостоятельно:

Задача № 1. Найти уравнение перпендикуляра, проходящего через точку К(1;-1;2), перпендикулярно плоскости

Ответ:

Задача № 2 Найти уравнение прямой, плоскостью проходящей через точку К(3;-4;7), перпендикулярно плоскости

Ответ:

Задача № 3 Найти уравнение плоскости, проходящей через точку К(-3;4;2) перпендикулярно прямой

Ответ:

Оглавление

1. Введение	3
2. Практическое занятие № 1. Вычисление определителей второго и третьего порядка.	3
3. Практическое занятие № 2. Решение систем линейных уравнений по правилу Крамера	5
4. Практическое занятие № 3. Скалярное произведение двух векторов и его приложение.	9
5. Практическое занятие № 4. Векторное произведение двух векторов и его приложение.	13
6. Практическое занятие № 5. Прямая линия на плоскости.	16
7. Практическое занятие № 6. Кривые второго порядка	18
8. Практическое занятие № 7. Прямая линия в пространстве	34
9. Практическое занятие № 8. Плоскость в пространстве	36
10. Практическое занятие № 9. Прямая и плоскость в пространстве.	37
11. Оглавление.	40

42