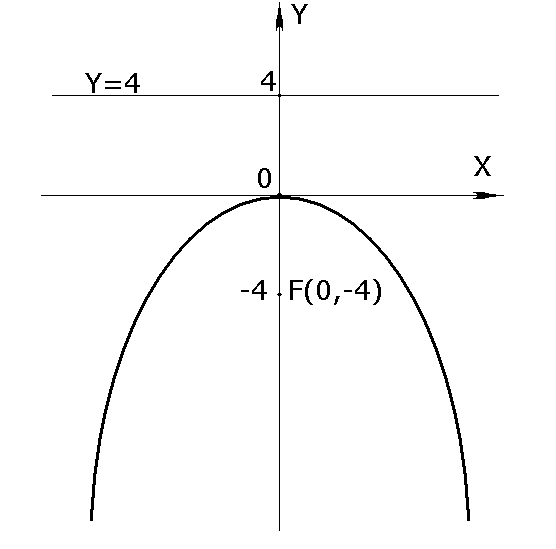6.4. Парабола.

Задача № 1. Определить координаты фокусов и составить уравнение директрисы параболы

Решение:

Сравнивая это уравнение с уравнением , находим, что 2p=4, откуда . Таким образом, точка - фокусы параболы, а прямая , т. е. x=-1 или x+1=0 – её директриса.

Ответ: (1;0)

Задача № 2. Фокусы параболы с вершиной в начале координат лежит в точке F(0;-4). Написать уравнение этой параболы.

Решение: Так как F(0;-4) с Оy, то данная парабола симметрична относительно оси Оy, а ветви её направлены вниз. Кроме того О (0;0) -вершина параболы. Следовательно искомое уравнение параболы запишется в форме . Поскольку, . Тогда, уравнение параболы будет

Задача № 3. Директрисой параболы с вершиной в начале координат служит прямая 2x+5=0

Написать уравнение и найти координаты фокуса параболы.

Решение: Так как директрисой параболы с вершиной в начале координат служит прямая 2x+5=0 или , то ее фокус имеет координаты

, поэтому искомая кривая симметрична относительно оси Оx F()и ветви ее направлены вправо (абсцисса фокуса положительна). Следовательно, уравнение параболы имеет вид

Так как то и уравнение параболы будет: , а координаты ее фокуса F(2,5;0)

Ответ: ; F(2,5;0)

Задача №4. Написать уравнение параболы, симметричной относительно оси Оy, с центром в начале системы координат, если она проходит через точку В(1;-2).

Решение:

Так как парабола симметрична относительно оси Оy и имеет вершину в начале системы координат, то ее уравнение имеет вид . Поскольку точка В(1;-2) лежит на параболе, то ее координаты удовлетворяют параболы, т.е. ,

Откуда , и, следовательно, - уравнение параболы.

Ответ:

Задача № 5. Найти высоту арки моста длиной 24м, если арка имеет вид параболы, уравнение которой

Решение:

Построим эскиз параболы в декартовой прямоугольной системе координат. Обозначим через h высоту моста, а через =24 - длину арки мосту. Тогда, А(12;-h)П: .

Так как точка А принадлежит параболе , то ее координаты удовлетворяют уравнению параболы. Это дает возможность вместо текущих координат (x;y) подставить координаты данной точки в уравнение параболы. Тогда имеем

Итак, высота арки моста 3 м.

Ответ: h=3

Задача № 6. Струя воды, направленная под углом к плоскости горизонта поднимается на высоту 2 м и падает в 12 м от наконечника шланга. Найти параболическую траекторию струи.

Решение: Свяжем параболическую траекторию струи с декартовой прямоугольной системой координат так, чтобы параболическая траектория была симметрична оси Оy, ветви были бы направлены вниз, а ее вершина лежала бы в начале координат.

Тогда уравнение такой параболической траектории имеет вид , точка А(6;-2)П: , следовательно, ее координаты удовлетво-ряют уравнению параболы. Подстановка координат точки А вместо текущих координатx и y параболы , дает равенство . Следовательно, - уравнение параболической траектории струи.

Ответ:

Решить самостоятельно:

Задача № 7. Сечение рефлектора плоскостью проходящей через ось рефлектора, есть парабола. Написать ее уравнение, если ширина рефлектора 30 см, а глубина 20 см, (ось рефлектора совпадает с осью Ox )

Ответ:

Задача № 8. Из отверстия, находящегося на поверхности земли вытекает вода струей, представляющей ветвь параболы . На каком расстоянии от края бака падает струя на землю, если высота отверстия

1,5 м ?

Ответ: 3 м.

Задача № 9. Осевое сечение параболического зеркала является параболой

Определить диаметр зеркала, если его «глубина» равна 18,75 см.

Ответ: 30 см.

Задача № 10. Камень брошенный под острым углом к плоскости горизонта, достиг наибольшей высоты 16 м., Описав параболическую траекторию, камень упал в 48 м., от точки бросания. Найти траекторию камня.

Ответ: .

Задача № 11 Найти параболу с вершиной в начале координат, если ее фокус лежит в точке а) F(3;0); б) F(-2;0); в) F(0;4); г) F(0;-)

Ответ: а); б); в); г)

Задача № 12 Найти параболы с вершиной в начале координат, если даны директрисы: а) ; б)x=-5 ; в) y=3 ; г) y=-2 ;

Ответ: а) ; б); в); г).

Задача № 13. Найти координаты фокуса и написать уравнение директрисы для каждой из парабол.

а) ; б); в); г). Построить эти параболы.

Ответ: а) F(2;0); x+2=0 ; б) F(-3;0); x-3=0 ; в) F(0;); 2y+5=0

г) F(0;-4); x-4=0

Задача № 14. Проверить, лежат ли точки А(2;-2) и В(1;2) на параболе

Ответ: А лежат, В не лежат.

Задача № 15. Написать уравнение параболы с вершиной в начале координат, симметричной относительно оси Оx и проходящей через точку

А(4;-2)

Ответ:

Задача № 16. Напишите уравнение параболы с вершиной в начале координат, если:

А) парабола расположена в верхней полуплоскости симметрично относительно оси ординат, а ее фокальный параметр равен 4;

Б) парабола расположена в нижней полуплоскости симметрично относительно оси ординат, а ее фокальный параметр равен 6;

В) парабола расположена в правой полуплоскости симметрично относительно оси ординат, а ее фокальный параметр равен 3;

г) парабола расположена в левой полуплоскости симметрично относительно оси ординат, а ее фокальный параметр равен 5.

Ответ а) ; б); в); г).

Практическое занятие № 7 на тему: