
- •Камышинский технологический институт (филиал)
- •Линейная и векторная алгебра, аналитическая геометрия
- •Введение.
- •2.2. Решение систем трех линейных уравнений с тремя неизвестными
- •Скалярное произведение двух векторов и его приложение
- •3.1 Нахождение работы постоянной силы на прямолинейном участке пути
- •3.2 Определение ортогональности двух векторов
- •3.3.Нахождение угла между векторами
- •Кривые второго порядка
- •6.1.Окружность
- •6.2.Эллипс
- •6.4. Парабола.
- •Прямая линия в пространстве.
- •Плоскость в пространстве
Кривые второго порядка
6.1.Окружность
Примеры:
|
Задача № 1. Написать уравнение окружности с центром С(4;-3), радиусом R=5 и построить её.
Решение.
Каноническое
уравнение окружнос-ти с
Следовательно,a = 4; b= -3; R= 5
Тогда уравнение
заданной окружности, будет
Ответ:
|
|
| |
|
Задача № 2. Определить координаты центра С и радиус R окружности
О |
|
| |
|
Задача № 3. Определить координаты центра С и радиус R окружности, заданной общим уравнением
Решение: выделяя полные квадраты в левой части уравнения, получим:
|
| ||
о кружности
кружности
![]()
 с центром в точке С(a;b)
и радиусом R,
показывает, что оно определяет окружность
с центром в точке С(-1;5)и радиусом R=5.
с центром в точке С(a;b)
и радиусом R,
показывает, что оно определяет окружность
с центром в точке С(-1;5)и радиусом R=5.
Ответ: С(-1;5), R=5
|
Задача № 4.
Написать уравнение
окружнос-ти, диаметром которой служит
отрезок MN,
где точка M Решение.
Координаты центра
С(a;b)
ок-ружности найдем как к
|
|
Следовательно С(-2;0). Радиус окружности
![]()
Тогда
![]() -
искомое решение
-
искомое решение
Ответ:
![]()
Решить самостоятельно:
Задача № 1. Составить уравнение окружности с центром в заданной точке С и данным радиусом R:
1) С
(4;-7), R
=5; 2) С (-6;3), R
=![]()
3) С (-1;0), R
=3; 4) С (0;-2), R
=![]()
5) С (-1;0),
R
=![]() ;
;
Ответ: 1)
![]()
2)
![]()
3)
![]()
4)
![]()
5)
![]()
Задача № 2. Для указанных окружностей определить координаты центра С и радиуса R:
1)![]()
2)
![]()
3)
![]()
Ответ: 1)
С(4;-6), R
=9; 2) С(-8;10), R
=13; 3) С(0;![]() )
,R
= -
)
,R
= -![]()
Задача № 3. Как
расположены по отношению к окружности
![]() следующие точки А(-1;-1);
В(2;-3); С(-3;5); Д(4;-1);
следующие точки А(-1;-1);
В(2;-3); С(-3;5); Д(4;-1);
Е (2;-2); F(5:7); G(1;0);
Ответ: точки А, Е и F лежат на окружности, точки В и С - вне окружности, точки Д и G-внутри окружности.
Задача № 4. Проходит ли окружность с центром в точке С(-5;7) и радиусом, равным 10, через точку М(-11;15) ?
Ответ: да.
Задача № 5. Окружность с центром в точке С(12;-5) походит через начало координат. Составить уравнение этой окружности.
Ответ:
![]()
Задача № 6. Известно,
что концы одного из диаметров окружности
находятся в точках М![]() (2;-7)
и М
(2;-7)
и М![]() (-4;3)
(-4;3)
Составить уравнение окружности.
Ответ:
![]()
6.2.Эллипс
Примеры:
Задача № 1. Найти
оси, вершины, фокусы и эксцентриситет
эллипса
![]()
![]() и построить его.
и построить его.
Решение:
Приведем данное
уравнение эллипса к коническому виду
![]() ,
для чего свободный член перенесем вправо
и разделим на него обе части уравнения.
В результате получим
,
для чего свободный член перенесем вправо
и разделим на него обе части уравнения.
В результате получим
![]() отсюда
отсюда
![]() .
.
Значит , длины полуосей равны соответственно a=5, b=3
А осей эллипса
имеют координаты:
![]() .
.
Вершины эллипса
имеют координаты:
![]()
Поскольку b![]() С
С![]()
По формуле
![]() находим эксцентриситет эллипса:
находим эксцентриситет эллипса:
![]()
П о
полученным данным построим эллипс:
о
полученным данным построим эллипс:
Ответ:
![]() ;
;
![]()
![]()
![]()
![]() ;
;
Задача № 2. Дан
эллипс
![]() ,
получаем
,
получаем
![]() .
Значит, длины полуосей равны соответственноa=5,
b=3,
а осей -
.
Значит, длины полуосей равны соответственноa=5,
b=3,
а осей -
![]() .
.
В ершины
же имеют координаты:
ершины
же имеют координаты:
![]() Так
как b>a,
то
Так
как b>a,
то
![]() и
и
![]() следовательно b
следовательно b![]()
![]()
Тогда
![]()
Откуда координаты
фокусов
![]()
![]() а эксцентриситет
а эксцентриситет
![]() ,
по полученным данным строим эллипс.
,
по полученным данным строим эллипс.
Ответ:
![]() ,
,
![]()
![]()
![]()
![]()
Задача № 3. Написать каноническое уравнение эллипса, проходящего через точку М(5;0), если фокальное расстояние равно 6.
Решение: Запишем
каноническое уравнение эллипса
![]()
Так как фокальное
расстояние
![]() то
С=3.
то
С=3.
По условию точка
М(5;0)
принадлежит эллипса. Поэтому при
подстановке координат точки М в уравнение
эллипса, получим
![]() ,
откуда
,
откуда
![]() .
Из равенства b
.
Из равенства b![]() находим
находим
![]() ,
,
Итак, искомым
уравнением эллипса будет уравнение
![]()
Решить самостоятельно:
Задача № 1. Напишите каноническое уравнение эллипса, если фокальное расстояние равно 8, а эллипс проходит через точку М(0;-3).
Ответ:
![]()
Задача № 2. Составить простейшее уравнение эллипса, фокусы которого лежат на оси ОX, если его полуоси равны 4 и 5.
Ответ:
![]()
Задача № 3. Найти координаты вершин, оси, фокусы и эксцентриситет эллипсов:
1)
![]() 2)
2)
![]()
Ответ: 1)![]() ;
;
![]() ;
;
![]()
![]()
![]()
2)
![]() ;
;![]() ;
;
![]()
![]()
![]()
Задача № 4. Найти координаты вершин, оси, фокусы и эксцентриситет эллипсов:
1)
9x![]() 2) 16x
2) 16x![]() 3) 25x
3) 25x![]()
Ответ : 1)
![]() ;
;![]() ;
;
![]()
![]()
![]()
2)
![]() ;
;![]() ;
;
![]()
![]()
![]()
3)![]() ;
;![]() ;
;
![]()
![]()
![]()
Задача № 5. Составить простейшее уравнение эллипса, у которого длина малой оси равна 24, а один из фокусов имеет координаты (-5;0)
Ответ:
![]()
Задача № 6. Расстояние между фокусами эллипса равно 30, а большая ось, лежащая на оси ОX, равна 34. Написать простейшее уравнение эллипса и найти его эксцентриситет.
Ответ:
![]() ;
;
![]()
Задача № 7. Составить простейшее уравнение эллипса, если известно,
Что один из фокусов
находится в точке (6;0), а эксцентриситет
![]()
Ответ:
![]()
Задача № 8. Составить простейшее уравнение эллипса, если:
между фокусами эллипса равно 6, а большая полуось равна 5;
малая полуось равна 3, эксцентриситет равен

большая полуось равна 10, эксцентриситет равен

Ответ: 1)
![]() ;
2)
;
2)![]() 3)
3)![]()
6.3. ГИПЕРБОЛА
Примеры:
Задача № 1. Найти
координаты вершин, оси, фокусы,
эксцентриситет и уравнения асимптот
гиперболы
![]() ,
и построить её.
,
и построить её.
Решение: Сравнивая
данное уравнение с каноническим
уравнением гиперболы
![]() .
Имеем
.
Имеем
![]() .Следовательно,
соответственноa=3,
b=4
. Тогда, действительно ось гиперболы
.Следовательно,
соответственноa=3,
b=4
. Тогда, действительно ось гиперболы
![]() ,
а мнимая
,
а мнимая
![]() ;
координаты вершин А
;
координаты вершин А![]() (-3;0),
А
(-3;0),
А![]() (3;0).
(3;0).
Далее,
![]() ;
следовательно, фокусами гиперболы
служат точки
;
следовательно, фокусами гиперболы
служат точки
![]() Эксцентриситет гиперболы вычисляется
по формуле, следовательно,
Эксцентриситет гиперболы вычисляется
по формуле, следовательно,
![]() .
Наконец, подставляя значения
.
Наконец, подставляя значения
а=3, b=4
в формулу
![]() ,
получаем уравнение асимптот гиперболы:
,
получаем уравнение асимптот гиперболы:
![]() и
и
![]() .
.
О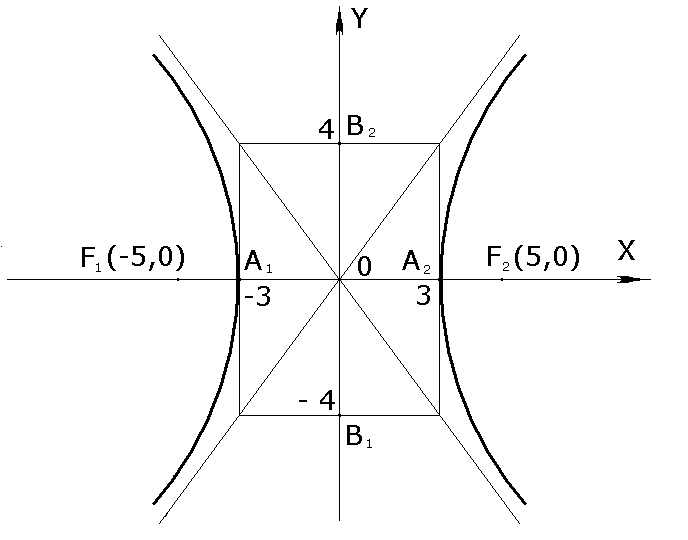 твет:
твет:
![]() ;
;![]() ;
А
;
А![]() (-3;0),
А
(-3;0),
А![]() (3;0),
(3;0),![]()
![]() ;
;![]()
Задача № 2. Найти
оси, вершины, фокусы, эксцентриситет и
уравнения асимптот гиперболы 16x![]() и построить её.
и построить её.
Решение:
Перенесем свободный член вправо и разделим на него все члены данного уравнения, В результате получим простейшее уравнение гиперболы.
![]() или
или
![]()
Так как знак «-»
стоит перед
![]() ,
то фокусы гиперболы расположены на осиOy,
а действительной осью
,
то фокусы гиперболы расположены на осиOy,
а действительной осью
![]()
![]() ,
принадлежащая оси Oy.
Сравнивая полученное уравнение с
уравнением
,
принадлежащая оси Oy.
Сравнивая полученное уравнение с
уравнением
![]() ,
имеем a=4,
b=3,
,
имеем a=4,
b=3,
![]() ,
координаты вершин
,
координаты вершин
![]() (0;-3),
(0;-3),![]() (0;3).
Далее, из формулы a
(0;3).
Далее, из формулы a![]() получаем c
получаем c![]() т.е.
с =
т.е.
с =![]() =5.
=5.
С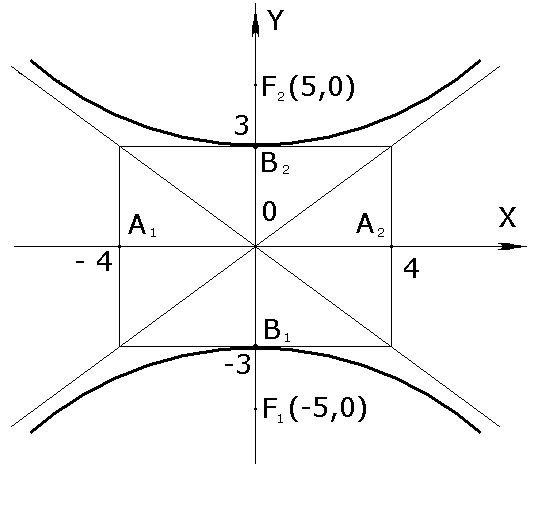 ледовательно,
фокусами гиперболы служат точки
ледовательно,
фокусами гиперболы служат точки
![]()
![]() Эксцентриситет гиперболы вычисляется
по формуле
Эксцентриситет гиперболы вычисляется
по формуле
![]() .
Наконец, подставляя значения a
= 4, b
= 3 в формулу
.
Наконец, подставляя значения a
= 4, b
= 3 в формулу
![]() ,
получаем уравнение асимптот гиперболы:
,
получаем уравнение асимптот гиперболы:
![]() .
.
Ответ:![]() ;
;
![]() ;
;![]() (0;-3),
(0;-3),
![]() (0;3).
(0;3).![]()
![]()
![]()
Задача № 3. Напишите каноническое уравнение гиперболы, если фокальное расстояние равно 30 и гипербола проходит через точку М(-9;0).
Решение:
Так как гипербола проходит через точку М(-9;0), то следовательно
М(-9;0)=А![]() (-9;0)
- вершина гиперболы, принадлежащая оси
Оx,
поэтому каноническое уравнение гиперболы
имеет вид
(-9;0)
- вершина гиперболы, принадлежащая оси
Оx,
поэтому каноническое уравнение гиперболы
имеет вид
![]() подставляя координаты точки М в указанное
уравнение, получаем
подставляя координаты точки М в указанное
уравнение, получаем
![]()
![]() а
а![]()
![]()
Так как фокальное
расстояние![]() ,
то с=15, используя формулу
,
то с=15, используя формулу
![]() получаем b
получаем b![]() .
Тогда
.
Тогда
![]()
Решить самостоятельно:
Задача № 1. Найти оси, вершины, фокусы, эксцентриситет и уравнения асимптот следующих гипербол.
1)
![]() 2)
2)
![]() и построить их.
и построить их.
Ответ: 1)![]() ;
;![]() ;
;![]()
![]()
![]()
![]() ,
,
![]()
2)![]() ;
;![]() ;
;![]() (0;-6),
(0;-6),![]() (0;6)
(0;6)![]()
![]()
![]() ,
,![]()
Задача № 2. Найти координаты вершин, оси, фокусы, эксцентриситет и уравнения асимптот следующих гипербол.
1)
![]() 2)
2)![]()
2)
![]() и
построить их.
и
построить их.
Ответ: 1)![]() ;
;![]() ;
;![]()
![]()
![]()
![]() ,
,
![]()
2)
![]() ;
;![]() ;
;![]()
3)![]() ;
;![]() ;
;![]() (0;-6),
(0;-6),![]() (0;6)
(0;6)![]()
![]()
![]() ,
,![]()
Задача № 3. Напишите уравнение гиперболы, если:
а) ее действительная полуось равна 4, а мнимая -14;
б) фокальное расстояние равно 16, а мнимая полуось -6;
в) фокальное
расстояние равно 6, а
![]() =1,5
=1,5
г) действительная
полуось равна 8, а
![]() ;
;
д) уравнение
асимптоты
![]() ,
а действительная полуось равна 3, а
,
а действительная полуось равна 3, а
![]()
Ответ: а)
![]() б)
б)![]() в)
в)![]()
г)
![]() д)
д)![]() е)
е)![]()
Задача № 4. Составить простейшее уравнение гиперболы, действительная ось которой равна 6, а расстояние между фокусами равно 8. Написать уравнение сопряженной гиперболы.
Ответ:
![]() ;
;![]()
Задача № 5. Напишите
каноническое уравнение гиперболы, зная,
что асимптоты её имеют уравнение
![]() ,
а фокусное расстояние равно 10.
,
а фокусное расстояние равно 10.
Ответ:
![]()
Задача № 6. Сумма
полуосей гиперболы равна 17, а эксцентриситет
![]() .
Написать простейшее уравнение гиперболы
и найти координаты её фокусов.
.
Написать простейшее уравнение гиперболы
и найти координаты её фокусов.
Ответ:
![]() ,
,![]()
![]()
Задача № 7.
Эксцентриситет гиперболы равен
![]() ,
а фокусами служат точки
,
а фокусами служат точки
![]()
![]()
Составить Уравнение гиперболы и написать уравнение её асимптот.
Ответ:
![]() ,
,![]() .
.


 центром в точке С(a;b)
и радиу-сом R
имеет вид
центром в точке С(a;b)
и радиу-сом R
имеет вид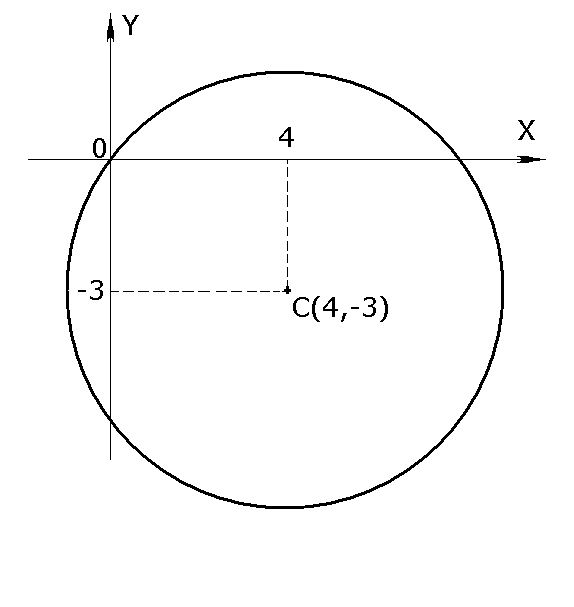
 и построить ее.
Решение: из к
и построить ее.
Решение: из к анонического
уравне-ния окружности с центром в
точке С(a;b)
и радиусом следует, что a
= 0; b=
-3;
анонического
уравне-ния окружности с центром в
точке С(a;b)
и радиусом следует, что a
= 0; b=
-3;


 (2;-3)
и точка N(-6;3)
и построить ее.
(2;-3)
и точка N(-6;3)
и построить ее. оординаты
точки, делящий отрезокMN
пополам:
оординаты
точки, делящий отрезокMN
пополам:
