А = | А1 – А2 | – амплитуда результирующего колебания равна разности амплитуд складываемых колебаний.
Биения
Если два складываемых гармонических колебаний одинакового направления мало отличаются по частоте, то возникают биения.
Биениями называют периодические изменения амплитуды колебания, возникающие при сложении двух гармонических колебаний с близкими частотами.
Пусть
х1 = A1 cos ωt
х2 = A2 cos (ω + Δω) t , тогда х = А′ cos ωt
Амплитуду А′ найдем по теореме косинусов: если А1=А2 ϕ01 = ϕ02 = 0 тогда
cos (x+y) = cos x·cos y – sin x·sin y 1 + cos2x = 2cos2x
A = |
A2 |
+ A2 |
+ 2A |
A cos |
ϕt = 2Acos( ωt 2) . |
(10.4) |
биен |
1 |
2 |
|
1 2 |
|
|
|
|
x = (2Acos( ωt |
2))cos ωt |
(10.5) |
||
уравнение биений
Т. к. Δω / 2 << ω , то (10.5) почти не изменяется за то время, когда cos ω t совершит полное колебание частоты изменения амплитуды биения в два раза больше частоты изменения косинуса ( т. к. берется по модулю ).
ωбиен = |
ω , |
(10.6) |
|||
тогда частота биений равна разности частот складываемых колебаний. |
|
||||
Tбиен = |
2π |
= |
2π |
. |
(10.7) |
ωT |
|
||||
|
|
ω0 |
|
||
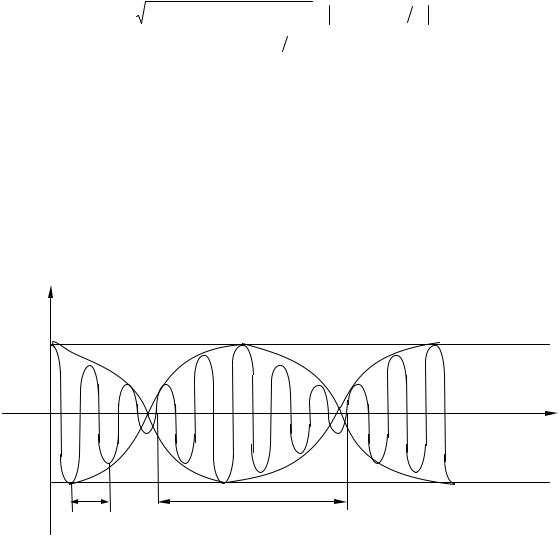
График результирующего колебания дают жирные линии, а огибающие их – график изменения с течением времени амплитуды.
х, Абиен
+ 2А
t
- 2А
ТТбиен
Рис. 10.2. Биения
Метод биений используется для настройки музыкальных инструментов, анализа слуха.
26