
изучение явлений взаимной индукции
.pdf
ФИЗИКО-ТЕХНИЧЕСКИЙ ИНСТИТУТ
КАФЕДРА ОБЩЕЙ И ТЕОРЕТИЧЕСКОЙ ФИЗИКИ
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
К ЛАБОРАТОРНОЙ РАБОТЕ № 29
«ИЗУЧЕНИЕ ЯВЛЕНИЯ ВЗАИМНОЙ ИНДУКЦИИ»
ТОЛЬЯТТИ 2007
ЛАБОРАТОРНАЯ РАБОТА № 29
ИЗУЧЕНИЕ ЯВЛЕНИЯ ВЗАИМНОЙ ИНДУКЦИИ
Цель работы: Определение коэффициента взаимной индукции двух катушек индуктивности.
Принадлежности: Генератор стандартных сигналов ГСС, цифровой вольтметр, осциллограф, две катушки индуктивности, сопротивление, скамья с измерительной линейкой.
1. При домашней подготовке к лабораторному занятию необходимо по любому источнику (Савельев И.В., Курс физики, т.2 или Трофимова Т.И., Курс физики) проработать следующий материал:
1.Электрический ток. Закон Ома.
2.Магнитный поток.
3.Явление электромагнитной индукции. С., § 60; Т., § 4.
4.Явление самоиндукции. С., §§64
5.Явление взаимной индукции. С., § 65.
6.Электрический ток при замыкании и размыкании цепи. С., § 67; Т., §51.
2.Проработать вывод расчётной формулы, приведённой в данной лабораторной работе.
3.Подготовиться к ответам на вопросы для тестового контроля по данной лабораторной работе.

I.КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
1.Основные понятия, законы и формулы
Электрическим током называется любое упорядоченное движение электрических зарядов.
Током проводимости называется упорядоченное движение свободных носителей заряда, возникающее под действием электрического поля в проводящих средах.
Силой тока называется скалярная физическая величина, равная отношению заряда, проходящего через поперечное сечение проводника за бесконечно малый промежуток времени, к величине этого промежутка.
Силой постоянного тока называется скалярная физическая величина, равная отношению заряда, проходящего через поперечное сечение проводника за конечный промежуток времени, к величине этого промежутка.
ЭДС называется скалярная физическая величина, численно равная работе сторонних сил по перемещению единичного положительного заряда вдоль всего рассматриваемого участка цепи.
Напряжением называется скалярная физическая величина, численно равная суммарной работе кулоновских и сторонних сил по перемещению единичного положительного заряда вдоль всего рассматриваемого участка цепи.
Закон Ома для замкнутой цепи I = εR ,
где R − суммарное сопротивление замкнутой цепи, ε − ЭДС в цепи, может быть наведено, например, в результате проявления явлений электромагнитной индукции, самоиндукции.
Явлением электромагнитной индукции называется явление, связанное с наведением вихревого электрического поля в замкнутом проводящем контуре при любых изменениях магнитного потока сквозь поверхность, ограниченную этим контуром.
Явление электромагнитной индукции подчиняется закону Фарадея:
ЭДС индукции, возникающая в замкнутом проводящем контуре при любых изменениях магнитного потока сквозь поверхность, ограниченную этим контуром прямо пропорциональна скорости этих изменений: εi = −Фт′ (t).
Магнитный поток сквозь поверхность, ограниченную контуром, может изменяться по трем причинам:
1.Магнитное поле переменно;
2.Происходит деформация контура;
3.Контур перемещается в магнитном поле.
Знак “−“ в законе Фарадея объясняется правилом Ленца: Индукци-
онный ток имеет такое направление, что его собственное магнитное поле противодействует причине вызвавшей появление этого индукционного тока.
|
Если мы имеем катушку с N витками, то закон Фарадея принимает |
вид: |
εi = −N Фт′ (t). |
|
Если магнитный поток сквозь поверхность, ограниченную контуром из- |
∆Ф
меняется равномерно, то закон Фарадея принимает вид: εi = − ∆tт ,
где ∆Фт – изменение магнитного потока за время ∆t .
∆Ф
Для случая катушки с N витками εi = −N ∆tт .
Если прямолинейный проводник движется с постоянной скоростью в однородном магнитном поле, то между его концами возникает разность потенциалов: ∆ϕ = B V A sin α ,
где α – угол между векторами скорости и индукции магнитного поля. Явлением самоиндукции называется явление возникновения индуциро-
ванного магнитного поля в цепи при изменениях в ней силы тока. Магнитный поток самоиндукции прямо пропорционален силе тока:
ФтS = I L ,

где L – индуктивность или коэффициент индуктивности. Индуктивностью называется скалярная физическая величина, численно
равная магнитному потоку самоиндукции при силе тока в один Ампер. Индуктивность зависит только от формы и размеров проводника, а так-
же от магнитных свойств окружающей среды.
Выведем закон Фарадея для самоиндукции:
εS = − dФdtтS εS = − d(Ldt I )= −[L′(t) I + I ′(t) L].
|
Когда индуктивность постоянна, т.е. L = const , то εS = −L I ′(t). |
|
Закон Фарадея для случая равномерного изменения силы тока в це- |
пи: |
εS = −L ∆I , |
|
∆t |
|
где ∆I – изменение силы тока за время ∆t . |
Физический смысл знака “−“ в законе самоиндукции (Правило Лен-
ца для самоиндукции): ЭДС самоиндукции является причиной возникновения тока самоиндукции, который будет противодействовать изменению основной силы тока в цепи, замедляя его возрастание или убывание.
Физический смысл коэффициента индуктивности: Индуктивность является мерой инертности проводника по отношению к изменению силы тока в нем.
Закон Фарадея для самоиндукции: ЭДС самоиндукции, возникающая в электрической цепи при любых изменениях силы тока в ней, прямо пропорциональна скорости этих изменений.
Рассмотрим простую электрическую цепь |
|
|
R, L |
||
При размыкании электрической цепи закон |
|
|
|
||
|
|
|
|||
|
|
|
|||
|
R |
|
|
|
|
изменения силы тока имеет вид: I = I0 e− |
|
t , |
|
|
|
L |
К |
||||
где I0 − сила постоянного тока до размыкания цепи. |
|
ε |
|||
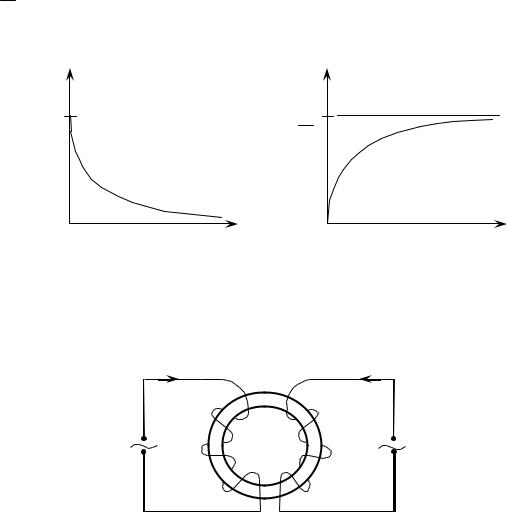
При замыкании электрической цепи закон изменения силы тока имеет вид:
|
ε |
|
|
− |
R |
t |
|
|
|
|
|
||||
I = |
|
|
−e |
|
L |
|
, |
|
|||||||
R |
1 |
|
|
|
|||
|
|
|
|
|
|
|
ε
где R − сила установившегося тока при замыкании цепи.
I
I0
Графики силы тока для обоих случаев.
I
ε
R
t t
Взаимной индукцией называется явление наведения ЭДС индукции в одном контуре, при изменении силы тока в другом.
Рассмотрим простейшую схему для изучения данного явления.
I1 I2
На тороид намотаны две катушки, на каждую из которых подается переменный ток. Каждый из этих токов будет создавать переменное магнитное поле. Эти магнитные поля будут пересекать соседние катушки, создавая в них магнитные потоки.
Магнитный поток сквозь вторую катушку, созданный магнитным полем первого тока будет равен: Ф21 = М21 I1 .
Аналогично магнитный поток сквозь первую катушку: Ф12 = М12 I2 ,
где M12 , M 21 – коэффициенты взаимной индукции; они зависят от формы, раз-
меров и взаимного расположения контуров (катушек), а также от магнитных свойств окружающей среды.
В общем случае М12 ≠ М21 .
Если окружающая среда является не ферромагнитной, то М12 = М21 .
Если контуры (катушки) не деформируются и, не перемещаются друг относительно друга, то М12 = М21 = const .
По закону Фарадея, ЭДС индукции в каждой из катушек прямо про-
порциональна первой производной по времени от магнитных потоков через
ε2 |
′ |
|
= −Ф21 (t) |
. |
|
эти катушки: |
′ |
|
ε1 |
= −Ф12 (t) |
|
Закон Фарадея для явления взаимной индукции, когда коэффициен-
ε2 = −M 21 I1′(t)
ты взаимной индукции постоянны: ε1 = −M12 I2′(t).
Формулировка закона: ЭДС взаимной индукции, возникающая в одном контуре, при изменении силы тока в другом контуре, прямо пропорциональна скорости этих изменений.
Закон Фарадея для явления взаимной индукции, для случая равно-
|
= −M 21 |
|
∆I |
1 |
|
ε2 |
|
|
|||
∆t |
|||||
мерного изменений сил тока в обоих контурах: |
|
|
|||
|
|
∆I2 |
|||
|
= −M12 |
|
|||
ε1 |
∆t |
||||
|
|
|
|||
где ∆I1 и ∆I2 изменения сил токов, соответственно, в первом и втором конту-
рах за время ∆t .
Физический смысл знака “−“ в законе взаимной индукции (Правило
Ленца для взаимной индукции): Электрический ток, индуцированный в одном контуре, имеет такое направление, что его собственное магнитное поле противодействует изменениям магнитного потока, созданного переменным током в другом контуре.
Для вычисления индуктивности системы, состоящей из катушек, необходимо рассмотреть суммарный магнитный поток (потокосцепление), пронизывающий поверхности витков каждой катушки и, который равен алгебраической сумме всех магнитных потоков, возникающих в системе
Ψ = Ψ11 + Ψ22 + Ψ12 + Ψ21 ,
где Ψ = L I − потокосцепление всей системы; Ψ11 = L1 I1 , Ψ22 = L2 I2 −
магнитные потоки через поверхности витков первой и, соответственно, второй катушек со стороны магнитный полей этих же катушек; Ψ12 = ±M12 I2 ,
Ψ21 = ±M 21 I1 − магнитные потоки через поверхности витков первой и, соот-
ветственно, второй катушек со стороны магнитный полей соседних катушек; знак « + » берётся, когда токи в катушках одного направления и, соответствен-
но, магнитные поля сонаправлены, в противном случае используется знак «−»;
L− индуктивность системы; L1 , L2 − индуктивности катушек; I, I1 , I2 − силы токов, соответственно, во всей системе, в первой и во второй катушках;
M12 , M 21 − коэффициенты взаимной индукции.
Рассмотрим случай одинаковых катушек, находящихся в неферромагнит-
|
|
~ |
|
|
|
|
L = L = L |
|
|
|
|||
|
1 |
2 |
, тогда формула потокосцепления примет вид |
|||
ной среде, т.е M12 |
= M 21 = M |
|||||
|
|
|
~ |
|
|
|
|
|
L I =(L ±M )(I1 + I2 ). |
|
|
||
При последовательном соединении (рис.1) I = I1 |
= I2 , следовательно, |
|||||
|
|
|
~ |
|
|
|
|
|
|
L = 2 (L +M ). |
|
|
|
При параллельном соединении (рис.2) I1 = I2 = |
I |
, следовательно, |
||||
2 |
||||||
|
|
|
|
|
||
= ~ +
L L M .

L1 |
L2 |
L1 |
L2 |
|
Рис. 1 Рис. 2
2. Вывод расчётной формулы
Установка состоит из двух электрически изолированных контуров: в пер-
вый контур входят генератор стандартных сигналов ГСС, катушка L1 , резистор
R и, подключенный параллельно к нему цифровой вольтметр; во второй − ка-
тушка L2 и осциллограф.
ГСС генерирует в первом контуре переменное напряжение
U1 =U0 cos(ω t), которое можно менять по частоте ω и амплитуде U0 и, сле-
довательно, через первую катушку проходит переменный электрический ток
I1 = I0 cos(ω t), который индуцирует в ней переменный магнитный поток.
Катушки L1 и L2 находятся на близком расстоянии, поэтому магнитный поток будет пронизывать и вторую катушку. Согласно закона взаимной индукции,
ЭДС индукции во второй катушке будет равна |
|
|
|
|
|
||||
|
ε2 = −M 21 |
dI1 |
= M 21 I |
0 ω sin(ω t) |
(1) |
||||
|
|
||||||||
|
|
dt |
|
|
|
|
|
||
где M 21 |
− коэффициент взаимной индукции, I0 |
= |
U0 |
− амплитуда силы тока в |
|||||
Z |
|||||||||
|
|
|
|
|
|
|
|
||

первой катушке, Z =  R2 + (ω L)2 − сопротивление переменному току, L −
R2 + (ω L)2 − сопротивление переменному току, L −
коэффициент индуктивности, соответственно, первой катушки, ω = 2 π ν −
циклическая частота, ν − частота переменного тока.
Из представленных формул следует, что амплитуда силы тока в катушке
L1 является величиной зависящей от частоты подаваемого тока, что является не желательным при выполнении данной работы, поэтому последовательно к катушке подключен резистор R , который обладает только активным сопротивлением. По двум последовательно соединенным элементам, как известно, протекает одинаковый ток, поэтому цифровой вольтметр подключен к резистору,
следовательно, I0 = UR0 − амплитуда силы тока на резисторе и, соответственно,
в первой катушке, R − сопротивление резистора, U0 − амплитуда напряжения
на резисторе.
ЭДС индукции во второй катушке подчиняется также гармоническому закону
ε2 =ε2,0 sin(ω t) |
|
(2) |
|
где ε2,0 − амплитуда ЭДС индукции во второй катушке. |
|
||
Сопоставляя формулы (1) и (2), получим |
|
|
|
ε2,0 = |
2 π ν M 21 |
U 0 |
(3) |
R |
|
||
|
|
|
|
В данной формуле величины: M 21 ,U0 , R , являются постоянными, поэтому из
(3) следует прямо пропорциональная зависимость между амплитудой ЭДС индукции во второй катушке и частотой переменного тока подаваемого на первую катушку.
Формула для расчёта коэффициента взаимной индукции следует (3)
M 21 |
= |
|
ε2,0 R |
(4) |
|
2 |
π ν U0 |
||||
|
|
|
Величина коэффициента взаимной индукции, в силу выше сказанного,
