Непрерывное преобразование.

Пусть имеется функция 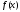и некоторая функция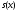- материнская функция. Рассмотрим числа вида

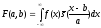(1)

Если 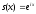, то в результате получаем обычное преобразование Фурье ( параметр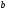не используется по понятной причине). Формула (1) определяет общееWavelet преобразование. Существует формула обратного преобразования, позволяющая в некоторых случаях восстановить исходную функцию по ее преобразованию. Однако основной смысл преобразования (1) заключается в другом. Величина 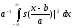не зависит от параметров. Это означает, что вектор, заданный функцией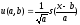, имеет постоянную длину в смысле пространства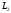. Предположим, что удалось найти такие значения параметров, для которых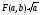достигает локального максимума. Это означает, что проекция функции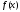на соответствующую функцию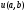имеет максимальное значение, поэтому графики этих функций аналогичны. Положив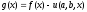, получим невязку, для которой решается такая же задача. В результате получаем приближение исходной функции функциями, порожденными с помощью функций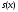. Это дает альтернативное описание исходной функции. В зависимости от того, какого рода особенности требуется обнаружить, выбирают вид материнской функции. При цифровой обработке, когда исходная функция задана лишь в отдельных точках, используется дискретное преобразование. Оказалось, что и в общем случае удается построить теорию, напоминающую теорию преобразования Фурье.

На практике, в качестве материнской функции при указанном подходе часто используют функцию 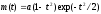( мексиканская шляпа). Константуопределяют из условия нормировки

Шкалирование

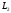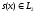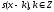Рассмотрим множество функций на вещественной оси. Пусть, причем функцииобразуют ортонормированную систему. Это означает, что

(2)

Такую функцию назовем шкалирующей. Например, любая функция, имеющая носитель внутри единичного интервала и норму равную 1, удовлетворяет условию (2). Обозначим через

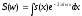
Предложение. Имеет место формула

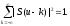(3).

Обратно, из (3) следует (2)

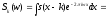
Доказательство. Имеем 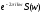. Поскольку преобразование Фурье является ортогональным преобразованием,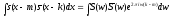. С учетом (2) это означает, что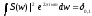. Далее, пусть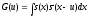. Преобразование Фурье этой функции есть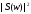. Теперь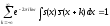, так как остальные слагаемы, равны нулю в силу (2). Заменим сумму интегралом и продолжим равенство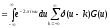. Заменим преобразование Фурье от произведения сверткой их образов. Преобразование от первого сомножителя есть он сам. Таким образом, равенство продолжается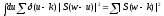. Обратное утверждение доказывается переписыванием формул в обратном порядке.

Важным примером материнской функции является функция, равная 1 на интервале 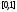и 0 в остальных точках. Такую функцию обозначим через.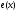

Wavelet-фильтрация. Детализация сигнала.

Введем обозначение: 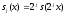для любой функции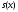. Положим.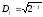

Предложение. Если выполнено условие ортогональности, то при фиксированном 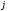функции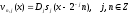образуют ортонормированную систему.

Доказательство. Имеем

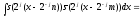
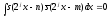при 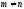. Нормированность проверяется очевидным образом с помощью замены переменных.

Обозначим через 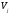линейное пространство, порожденное функциями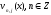. Потребуем, чтобы имело место включение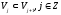. Это весьма жесткое ограничение. Оно выполнено, например, для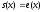. Для произвольной функции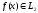положим

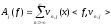(1)

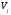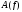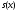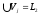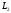- проекция функции на пространство . Коэффициенты разложения это и есть дискретныеwavelet преобразования. Чем больше индекс пространства, тем более точное приближение исходной функции с помощью получаем. Эта процедура и называется детализацией. Наложим наеще одно дополнительное условие: потребуем, чтобы. Последнее означает, что каждую функцию изможно приблизить с произвольной точностью подходящей функцией из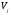. 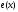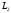Заметим, что это выполнено для функции, поскольку каждую функцию изможно приблизить ступенчатой функцией. Как следствие получим, что это верно и для произвольной функции с носителем на интервале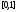, с помощью которой можно приблизить функцию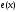. Положим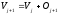, где второе слагаемое есть ортогональное дополнение к первому. Теперь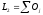- прямая сумма попарно ортогональных пространств. 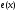Длятак получается базис Хаара, о котором будет рассказано позже.