
- •Минобрнауки россии
- •Содержание.
- •1. Цифровые фильтры. Основные понятия
- •Рекуррентные системы
- •Фильтры.
- •Фильтры с конечным временем отклика.
- •Фильтры с бесконечным временем отклика
- •2. Z-преобразование. Фильтры первого порядка z-преобразование
- •Идеальный фильтр
- •Фильтр первого порядка
- •3. Фильтры второго порядка Определение фильтра второго порядка
- •Фильтры высших порядков
- •Фильтр Баттеруорта (Butterworth)
- •4. Фильтры Баттеруорта Отыскание параметров фильтра
- •Полосовой фильтр
- •Полосовой фильтра как последовательное соединение фильтров высоких и низких частот
- •Тангенциальный фильтр
- •5. Fir фильтры Полосовой фильтр на основе фильтра низких частот
- •Фильтр как осциллятор
- •Фазовый сдвиг сигнала в результате фильтрации
- •Фильтры с конечным временем отклика
- •Проектирование fir фильтров. Сглаживающие окна
- •6. Квадратурный зеркальный фильтр Проектирование fir фильтра на основе аппроксимации
- •Квадратурный зеркальный фильтр
- •7. WaveLet-преобразования
- •Непрерывное преобразование.
- •Шкалирование
- •Wavelet-фильтрация. Детализация сигнала.
- •Wavelet фильтрация
- •Заключение
4. Фильтры Баттеруорта Отыскание параметров фильтра
В
левой и правой частях в знаменателе
находятся многочлены от переменной z.
Найдем корни этих многочленов. Множество
корней по построению инвариантно
относительно замены
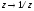 .
Для устойчивости фильтра нужно, чтобы
корни находились внутри единичного
круга. Для отыскания нулей знаменателя
в правой части получим уравнение
.
Для устойчивости фильтра нужно, чтобы
корни находились внутри единичного
круга. Для отыскания нулей знаменателя
в правой части получим уравнение
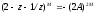 ,
откуда
,
откуда
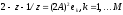 ,
где
,
где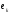 - корень степени
- корень степени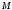 из -1. Каждое из этих уравнений сводится
к квадратному уравнению. Найдем корни
этих уравнений и выберем те из них,
которые по модулю меньше единицы.
Составим произведение
из -1. Каждое из этих уравнений сводится
к квадратному уравнению. Найдем корни
этих уравнений и выберем те из них,
которые по модулю меньше единицы.
Составим произведение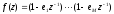 .
Проблема может возникнуть лишь в случае,
когда среди корней окажется корень
равный по модулю 1. Такая ситуация не
возможна, так как в противном случае
.
Проблема может возникнуть лишь в случае,
когда среди корней окажется корень
равный по модулю 1. Такая ситуация не
возможна, так как в противном случае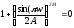 для некоторого
для некоторого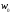 .
.
Фильтр высоких частот
Рассмотрим
функцию
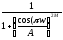 .
Она получена заменой из предыдущей
.
Она получена заменой из предыдущей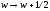 .
Это передаточная функция фильтра высоких
частот. С другой стороны, из выражения
.
Это передаточная функция фильтра высоких
частот. С другой стороны, из выражения при указанной замене получим
при указанной замене получим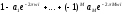 .
Это означает, что фильтр высоких частот
можно получить из фильтра низких частот
заменой знака у коэффициентов с нечетными
индексами.
.
Это означает, что фильтр высоких частот
можно получить из фильтра низких частот
заменой знака у коэффициентов с нечетными
индексами.
Полосовой фильтр
Рассмотри
выражение
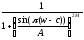 ,
где
,
где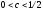 .
Очевидно, что эта функция достигает
своего максимума при
.
Очевидно, что эта функция достигает
своего максимума при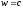 .
Это означает, что передаточная функция
изображает полосовой фильтр. При замене
в выражении
.
Это означает, что передаточная функция
изображает полосовой фильтр. При замене
в выражении
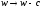 получим фильтр с комплексными
коэффициентами. Формально - это решение
задачи, однако использование комплексного
фильтра для фильтрации вещественного
сигнала не очень удобно. Поэтому
используют выражение вида
получим фильтр с комплексными
коэффициентами. Формально - это решение
задачи, однако использование комплексного
фильтра для фильтрации вещественного
сигнала не очень удобно. Поэтому
используют выражение вида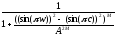 .
Для четного
.
Для четного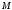 .
Оно снова достигает максимума при
.
Оно снова достигает максимума при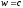 .
Используя ту же технику, что и в предыдущем
случае, после замены
.
Используя ту же технику, что и в предыдущем
случае, после замены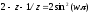 снова сведем задачу к отысканию корней
квадратного уравнения.
снова сведем задачу к отысканию корней
квадратного уравнения.
Полосовой фильтра как последовательное соединение фильтров высоких и низких частот
При последовательном соединении фильтров высоких и низких частот их передаточные функции перемножаются. В результате получаем передаточную функцию полосового фильтра. Это наиболее простой способ получения полосового фильтра, но при этом повышается размерность.
Тангенциальный фильтр
Для случай фильтра низких частот в синусоидальном фильтре на конце интервала не достигался 0. Рассмотрим функцию
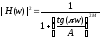 .
Теперь получается передаточная функция
с нулем при
.
Теперь получается передаточная функция
с нулем при
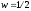 .
Если
.
Если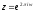 ,
то
,
то .
Используя тот же прием, получим, что
.
Используя тот же прием, получим, что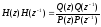 .
Для отыскания коэффициентов многочленов
в числителе и знаменателе рассматривают
нули и полюса передаточной функции.
.
Для отыскания коэффициентов многочленов
в числителе и знаменателе рассматривают
нули и полюса передаточной функции.
5. Fir фильтры Полосовой фильтр на основе фильтра низких частот
В предыдущей лекции было показано, каким образом можно построить различные фильтры. Оказывается, любой из таких фильтров можно получить на основе фильтра низких частот с помощью универсальной процедуры.
Сдвиг

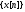 с преобразованием Фурье
с преобразованием Фурье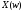 .
Рассмотрим новую последовательность
.
Рассмотрим новую последовательность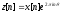 .
По определению
.
По определению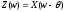 .
Если нам нужен полосовой фильтр, можем
поступить следующим образом. Сдвиг
осуществляется генератором на основе
осциллятора, о котором будет сказано
ниже. Обратный сдвиг осуществляется
так же.
.
Если нам нужен полосовой фильтр, можем
поступить следующим образом. Сдвиг
осуществляется генератором на основе
осциллятора, о котором будет сказано
ниже. Обратный сдвиг осуществляется
так же.
Непосредственное
применение указанного способа не удобно,
поскольку приходится работать с
комплексными числами, и в результате
обратного сдвига получается, как правило,
комплексный сигнал. Выход заключается
в преобразовании
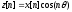 .
В результате
.
В результате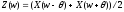 .
Если исходный сигнал имеет ограниченный
спектр и
.
Если исходный сигнал имеет ограниченный
спектр и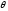 выбран так, что носители
выбран так, что носители и
и не пресекаются, задача решается без
применения комплексных чисел. Например,
пусть спектр
не пресекаются, задача решается без
применения комплексных чисел. Например,
пусть спектр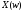 находится
в интервале 2kHz-4kHz,
и требуется получить лишь часть сигнала
в диапазоне 2.5kHz-3.5kHz.
Выбираем
находится
в интервале 2kHz-4kHz,
и требуется получить лишь часть сигнала
в диапазоне 2.5kHz-3.5kHz.
Выбираем
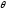 =3kHz
и используем фильтр низких частот с
полосой пропускания 0.5kHz.
После обратного сдвига придется
использовать еще один фильтр низких
частот с полосой пропускания 3.5kHz.
=3kHz
и используем фильтр низких частот с
полосой пропускания 0.5kHz.
После обратного сдвига придется
использовать еще один фильтр низких
частот с полосой пропускания 3.5kHz.
