
- •Введение
- •1.Стандартное преобразование Фурье
- •1.1. Пример анализа с использованием преобразования Фурье.
- •1.3. Анализ применимости преобразования Фурье.
- •2. Кратковременное преобразование Фурье
- •2.1. Общие сведения.
- •2.2. Анализ применимости кратковременного преобразования Фурье.
- •2.3. Принцип Гейзенберга.
- •3. Непрерывное wavelet-преобразование и анализ со многими разрешениями.
- •3.1.Общие сведения
- •3.2.Определение непрерывного wavelet - преобразования
- •3.3. Примеры материнских wavelet-ов
- •3.4. Локализующие свойства и интерпретация
- •3.5. Свойства cwt
- •3.6. Примеры непрерывного wavelet-преобразования
- •3.7. Дискретизация непрерывного wavelet-преобразования.
- •3.8. Практическое использование непрерывного wavelet-преобразования
- •4. Дискретное wavelet-преобразование
- •4.1. Кратномасштабный анализ
- •4.2. Wavelet-ряды дискретного времени
- •4.3. Матричное описание дискретного wavelet-преобразования
- •4.4. Описание dwt посредством банков фильтров.
- •5. Применение дискретного wavelet-преобразования.
- •5.1. Применение wavelet-преобразования для сжатия сигнала.
- •5.2. Удаление шума из сигнала.
- •6. Адаптивные ортогональные преобразования.
- •6.1. Пакеты вейвлетов.
- •7. Работа с приложением gui wavemenu пакета программ matlab
- •7.1 Описание Wavemenu
- •7.1.1. Вызов Wavemenu
- •7.1.2. Структура Wavemenu
- •7.1.3. Меню для разделов Wavemenu
- •7.1.4. Экспорт и импорт информации из Wavemenu
- •7.2 Использование Wavemenu для обработки сигналов
- •7.2.1. Получение информации по конкретным wavelet-ам
- •7.2.2. Использование дискретного wavelet-преобразования
- •Очистка сигнала от шумов на основе dwt
- •Сжатие сигнала на основе dwt в Wavemenu
- •7.2.3. Использование разложения по wavelet-пакету
- •Очистка сигнала от шумов с использованием wavelet-пакет
- •Сжатие сигнала с использованием wavelet-пакет
- •7.2.4 Работа с непрерывным wavelet-преобразованием
- •Литература
- •197376, С.-Петербург, ул. Проф. Попова, 5
Сжатие сигнала на основе dwt в Wavemenu
При сжатии сигнала используют следующую схему: производится wavelet-преобразование исходного сигнала, после чего запоминаются только значащие коэффициенты, то есть те, которые больше некоторого заданного порога. Восстановление сигнала производится при помощи обратного wavelet-преобразования, при этом пропущенные коэффициенты заменяются нулями.
Графический инструмент позволяет производить сжатие с автоматическим (Automatic thresholding) или ручным (Manual thresholding) выбором порога. В последнем случае порог для каждого уровня разложения можно задавать отдельно.
В качестве сигнала для сжатия будем использовать тот же сигнал noischir.mat
Для решения задачи сжатия сигнала следует вызвать соответствующий инструмент нажатием кнопки "Compress", размещённой в середине правой колонки окна, под кнопкой "Analyze".
При автоматическом выборе порога на самом левом графике отображаются процент сохранённой энергии сигнала и процент нулевых коэффициентов в зависимости от порога (вертикальная пунктирная линия).
Зададим автоматический выбор порога (automatic thresholding). Значением порога по умолчанию будет число, при котором процент сохранённой энергии сигнала будет равен проценту нулевых коэффициентов, в нашем случае, этот порог будет равен 5,326.
Если нажать кнопку "Compress", то после паузы для вычисления исходный сигнал будет показан красным, а сжатый сигнал — жёлтым цветом.
Легко видеть, что в процессе сжатия сигнала мы удалили большинство коэффициентов (81,44%), сохранив в оставшихся 81,52% энергии сигнала.
При закрытии окна инструмента для сжатия сигнала (кнопка "Close") опять появится диалог с вопросом об обновлении синтезированного (сжатого) сигнала.
7.2.3. Использование разложения по wavelet-пакету
При разложения сигнала по wavelet-пакету на каждом уровне последующей фильтрации подвергается не только низкочастотная, но и высокочастотная составляющая.
Wavelet-пакетом является любой подграф G полного графа разложения, удовлетворяющий следующим свойствам:
корень дерева принадлежит G;
в каждой из вершин граф G либо делится на две части, либо прерывается.
Сигнал, получающийся в каждом узле дерева wavelet-пакета можно интерпретировать как выход некоторого полосового фильтра. Сложность вычисления по полной схеме пропорциональна NlogN, где N является длиной сигнала.
Для
экономии вычислений и повышения качества
разложения вводится аддитивная функция
стоимости E( s),
такая что
![]() и
и
![]() ,
,
где si - коэффициенты разложения в i-м узле дерева.
Далее, на основе введённой функции стоимости определяется наилучший подграф полного дерева. Если суммарная функция стоимости потомков узла меньше, чем функция стоимости предка, то они включаются в подграф, в противном случае, данный узел становится терминальным, то есть последующее разбиение этого узла не производится.
Таким образом, можно адаптировать разложение к сигналу. Отметим, что такая адаптация не требует обучения или знания статистических свойств сигнала.
Функции стоимости, используемые в GUI Wavemenu для определения наилучшего подграфа:
Shannon -
 , log(0) принимается равным 0;
, log(0) принимается равным 0; Threshold- число отсчётов, по абсолютному значению больших, чем заданный порог e;
Norm -
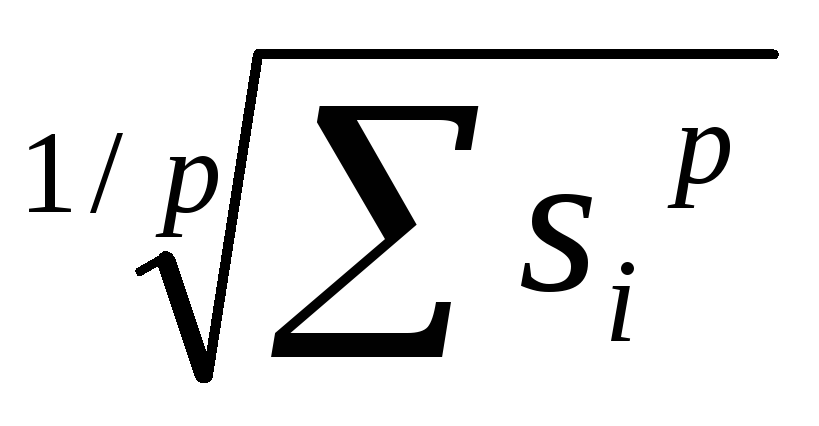 , 1
p < 2
;
, 1
p < 2
; Log Energy -
 ,
log(0) принимается равным 0;
,
log(0) принимается равным 0; SURE -
 ,
N - количество отсчётов;
,
N - количество отсчётов; User- функция стоимости задаётся в MAT-файле.
Для анализа и синтеза сигналов, используя разложение по wavelet-пакету, необходимо выбрать пункт "Wavelet Packet 1-D" в главном меню. Появится панель инструментов разложения одномерного сигнала по wavelet-пакету (рис.22).

Рис. 22. Панель инструментов разложения одномерного сигнала по wavelet-пакет.
