
1. Рассчитаем эти вероятности:
pk (B1)= 0,7*0,6= 0,42 , если ваза окажется 1-го типа,
pk (B2)= 0,3*0,3= 0,09, если ваза окажется 2-го типа.
Следовательно, вероятность вытащить красный шар в общем случае:
pk = pk (B1) + pk (B2) = 0,51.
Аналогичным образом можно подсчитать, что вероятность вытащить чёрный шар pч=0,49.
pч(B1) = 0,7*0,4= 0,28 , если ваза окажется 1-го типа,
pч(B2) = 0,3*0,7= 0,21, если ваза окажется 2-го типа.
Следовательно, вероятность вытащить красный шар в общем случае:
pч = pч(B1) + pч(B2) = 0,49.
|
ваза 1-го типа |
ваза 2-го типа |
Общий случай |
|
pk (B1)= 0,42 |
pk (B2)= 0,09 |
pk = 0,51 |
|
pч(B1) = 0,28 |
pч(B2) = 0,21 |
pч = 0,49 |
2. Пусть вытащенный шар оказался красным (чёрным). Какое действие следует выбрать: d1 или d2? Для ответа на этот вопрос нужно знать вероятности принадлежности ваз к 1-му и 2-му типам после получения дополнительной информации. Эти вероятности позволяет определить формула Байеса.
Например, мы вытащили красный шар. Какова после этого вероятность того, что перед нами стоит ваза 1-го типа?
Формула Байеса позволяет оценить p(Bi/k) p(Bi/ч), где i=1,2, используя все прочие вероятности:
Для красного шара из вазы 1-го типа - p(B1/k)= pk (B1)* pk / pk (B1)* pk + pk (B2)* pk
Для черного шара из вазы 1-го типа - p(B1/ч)= pч (B1)* pч / pч (B1)* pч + pч (B2)* pч
Решение:
1. Считаем p(B1/k) - вероятность того, что ваза окажется 1-го типа после вытаскивания красного шара
p(B1/k)=0.42*0.51 / 0,42*0,51+0,09*0,51=0,2142 / 0,2601=0,82
2. Считаем p(B1/ч) - вероятность того, что ваза окажется 1-го типа после вытаскивания чёрного шара
p(B1/ч)=0,28*0.49 / 0,28*0.49+0,21*0,49=0,1372 / 0,2401=0,57
3. Считаем p(B2/k) - вероятность того, что ваза окажется 2-го типа после вытаскивания красного шара;
p(B2/k)=1- p(B1/k)=0,18
4. Считаем p(B2/ч) - вероятность того, что ваза окажется 2-го типа после вытаскивания чёрного шара.
p(B2/ч)=1- p(B1/ч)=0,43
Вывод: Следовательно, выбираем действие d1 с вероятностью 0,82 того, что ваза окажется 1-го типа после вытаскивания красного шара
Теперь имеем всю информацию, необходимую для принятия решений.
На рисунке 4.2 показаны две основные ветви дерева решений, причём верхняя повторяет дерево решений на рисунке 4.1. Квадрат 1 слева соответствует первому решению - вытаскивать шар или нет. Случаю отказа от вытаскивания шара соответствует нижняя ветвь, начинающаяся со случайного события (круг). В квадратах 2,3,4 принимаются решения о выборе одной из двух стратегий: d1 или d2. Далее всё решает случай (круги).
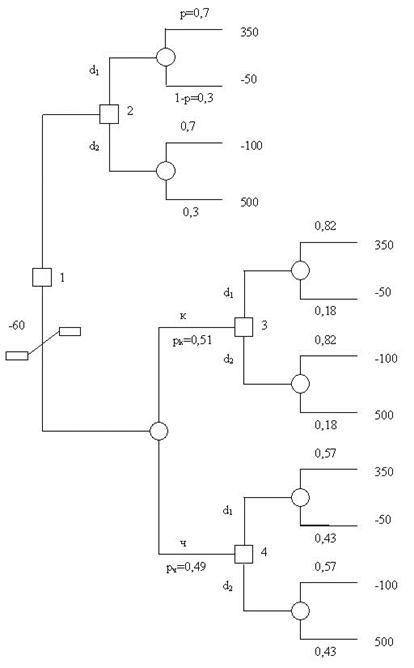
Рисунок 4.2 – Дерево решений
Существует три простых правила выбора оптимальной (по критерию максимума ожидаемой полезности) последовательности решений на основе дерева решений.
1) идти от конечных ветвей к его корню;
2) там, где есть случайность (кружок), находится среднее значение:
U (d1)=0,82*350 + 0,18*(-50)=287-9=278 д.е;
U (d2)= 0,18*500 + 0,82*(-100)=90-82=8 д.е.
3) там, где есть этап принятия решений (квадратик), выбирается ветвь с наибольшей ожидаемой полезностью, а другая отсекается двумя чёрточками
Применим эти правила к дереву решений, представленному на рисунке 4.2. В результате получим дерево решений, показанное на рисунке 4.3.
278
278
178
178
194
Рисунок 4.3 – «Сворачивание» дерева решений
На этом рисунке над кругами указаны средние значения полезности, двумя чёрточками отсечены ветви с меньшим значением ожидаемой полезности. Наилучший вариант действий: шар не вытаскивать и выбирать действие d1. Этот вариант соответствует самому верхнему пути дерева решений на рисунка 4.3. Такая процедура нахождения оптимального пути на деревьях решений получила название «сворачивание» дерева решений.
Деревья решений при заданных числовых значениях вероятностей и исходов позволяют осуществить выбор той стратегии (последовательности действий), при которой достигается наибольший выигрыш, т.е. достигается максимум функции полезности ЛПР.
