1). Линейная зависимость. (y(X))

(3)

в каждой точке устанавливается связь между х и у

- теоретическая функция y – экспериментальное значение

В пределах проведенного эксперимента мы можем иметь следующее данные.

Экспериментальный интервал значений Х

Интервал значений Y.

Коэффициент К входящий в уравнение (3) называется угловым коэффициентом который равен тангенсу угла наклона прямой к оси абсцис:

2). Показательная функция.

(4).

Возьмем натуральный логарифм от уравнения (4).

(5)

Если поле точек может быть описано функцией (4), то график поля точек в логарифмических координатах будет близок к зависимости (5)

In yi	xi

3). Степенная функция.

(6)

Для определения параметров аппроксимации а и в, возьмем логарифм от обоих частей равенства (6).

(7)

Для построения графика в логарифмических координатах предпочтительно по данным исходных таблиц строиться:

In yi	xi

4). Поленомальная аппроксимация

см вопрос № 16

Вопрос №17. Характеристики переменного гармонического тока и напряжения.

Переменным называется ток, сила которого I является функцией времени I(t).

Силой тока в общем случае называется производная:

, т.е. количество электрических зарядов протекающих через поперечное сечение проводника за единицу времени.

В случае, если протекающий заряд пропорционален:

, то производная примет вид

широкое применение на практике находит гармоническая зависимость переменного тока или напряжения от времени:

- круговая или циклическая частота

ν – физическая частота, измеряемая в Герцах [Гц]

Кроме гармонического тока (напряжения) часто используются периодические или импульсный ток (напряжение).

Ток, сила которогоI есть некоторая функция времени, называется переменным током. Аналогично можно внести понятие переменного напряжения, когда разность потенциалов между точками цепи есть функция времени.

τ – время релаксации напряжения.

;

; ,

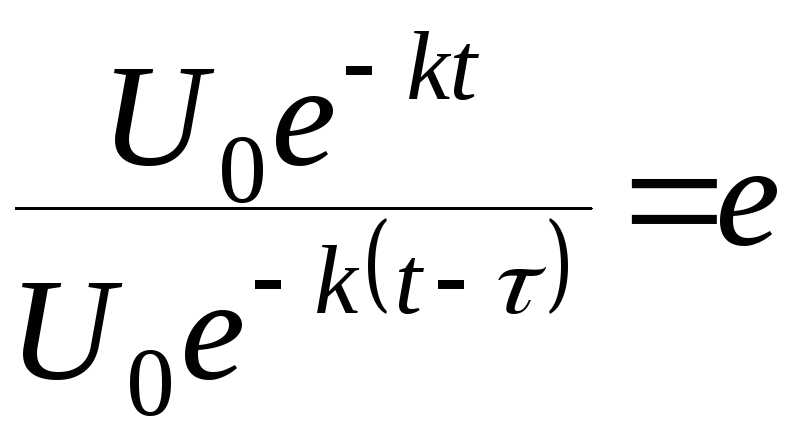
- скважность импульсов (количество сигналов в единицу времени).

- длина импульса.

Периодический сигнал согласно теореме Фурье, можно представить в виде суммы гармоник (разложение функции в ряд Фурье или в интеграл Фурье). Число гармоник зависит от формы импульсов, в частности, для строго прямоугольного импульса п→∞.

Верхняя частота гармоники, т.е максимальное значение частоты гармоники обратно пропорционально времени нарастания переднего фронта.

Вопрос №18. Электромеханические преобразователи. Уравнения шкалы электроизмерительных аналоговых приборов.

Устройство преобразователей, позволяющее значение одной физической величины преобразовать в значение другой физической величины. В частности в виде некоторого эквивалентного электрического сигнала.

Такими преобразователями являются аналоговые стрелочные электроизмерительные приборы, которые преобразовывают энергию электромагнитного поля в механическую энергию поворота подвижной части прибора и жестко связанной с ней указательной стрелкой, которая в виде показания дает отклонение стрелки на некоторый угол α выраженный в градусах или делениях шкалы. Зная номинальное значение измеренной величины Yn и общее количество делений шкалы N можно найти цену деления шкалы:

Величина обратная Х называется чувствительностью прибора:

поворот подвижной части прибора на некоторый угол α связан с воздействием на нее вращающего момента М, которое согласно уравнению Лагранжа второго рода может быть найдено как производная электромагнитной энергии, преобразующей в данном устройстве по углу поворота стрелки указателя

В самом общем виде суммарная электроэнергия запишится:

Имеется достаточно большое количество различных систем электроизмерительных приборов.

Наиболее употребляемые:

• Магнитоэлектрическая

• Электромагнитная

• Электродинамическая

• Электростатическая

• Индукционная

• Угловая и т.д.

В приборах того или иного типа преобладающим может являться то или иное слагаемое равенства (1). В этом случае другим слагаемым можно пренебречь.

Показано что вращающий момент М может зависеть от электрической величины I тремя способами:

1. (2)

2. (3)

3. (4)

Равенство (2) – магнитоэлектрические приборы (момент может быть пропорционален произведению двух электрических величин).

Равенство (3) реализуется в приборах электродинамической системы.

Равенство (4) – в приборах электромагнитных, электростатических и других системах.

Шкала аналогового электроизмерительного прибора могут быть двух типов:

• С началом шкалы у левого конца подвижная часть поворачивается всегда по часовой стрелки.

• В зависимости от направления тока в измерительной катушке подвижная часть поворачивается как по часовой, так и против часовой.

Воздействие только одного момента на подвижную часть на позволяет провести измерения электрической величины Y поскольку стрелка прибора под воздействием сколь угодно малого момента М отклониться до упора. Поэтому наряду с вращательным моментом на подвижную часть действует еще и момент упругой возвращающей силой спиральной пружины. Обычно этот момент пропорционален углу закручивания.

При некотором значении электрических величины на входе прибора между моментами М и Мn устанавливается равновесие, т.е.

В зависимости от вида момента (2), (3) или (4) получаем то или иное уравнение шкалы.

Вопрос №16. Полиномная аппроксимация. Метод наименьших квадратов.

Рассмотрим внешнею функцию аппроксимации описывает лишь монотонные возрастания или убывание функции , не позволяя выделить на поле точек экстремального их поведения

Полиномом п-ного порядка называется выражения

Рассмотрим полином второго порядка

Задачей аппроксимации является нахождение коэффициента полинома, которую требуется провести таким образом, чтобы полином наилучшим образом проходил в близи всех эксперимент точек.

В качестве критерия оптимизации возьмем лианеризацию функционала F следующего вида.

(1)

п – общее количество экспериментальных точек

Функциональная F – есть дисперсия определения рассеяние экспериментальных точек от теоретической кривой.

Коэффициент полинома будем находить исходя из условия минимизации функционала F.

Проведем некоторое преобразование формулы (1).

Введем переменные (2).

Тогда

(3)

Для нахождения коэффициента полинома условия минимизации (3) записываются в виде:

Полученная система уравнения позвонит найти искомый коэффициент полинома:

(4)

Преобразует полученную систему:

(5)

Введем обозначения:

подсчитываются по экспериментальным данным

(6)

Система линейных неоднородных уравнений.

Система (6) решает любым известным способом, например методом определителей (или Крамара).

, ,

D0 основной определитель системы из коэффициентов неизвестных:

Вопрос №35. Мосты переменного тока. Условие равновесия.

Кроме активных сопр. в качестве пассивных элементов электрических цепей исп. катушки индуктивностиL и конденсаторы емкости C. Реактивные элементы L и C прим. в цепи переменного тока частоты w, причем реактивные сопр. этих элементов опр. по формулам X_C = 1/wC, X_L = wL. Реальные реактивные элементы конденсаторы и катушки кроме емкости и индуктивности хар. нек-рыми активными сопр., наз. сопр. потерь. R_L – активное сопр. провода, намотанного на катушку. Конденсаторы также обл. нек-рым малым сопр. потерь., которое в зависимости от вел. вкл. в экв. сх. конденсатора либо посл. (малые потери) либо пар. (большие потери), при этом пластины C шунтируются акт. сопр.

Рассмотрим одинарный мост переменного тока. В качестве индикатора прим. либо аналоговый высокоомный вольтметр либо осциллограф с лин. разверткой. При этом точки a и b сх. вкл. на верт. откл. пл. (вх. Y). При вкл. ГЛИН на экр. набл. sin сигн. нек-рой амплитуды. U_ab = U₀sin wt. Обычно в два плеча мост. сх. вкл. переменные активные сопр., с пом. к-рых достигается равновесие моста, которое выражается в выравнивании потенциалов a и b. При этом амплитуда U₀ уменьшается и при полном уст. равновесия на экр. видна только гор. полоса, созданная сигн. лин. развертки. В отл. от моста пост. тока в этой сх. необх. 2 переменных резистора. Выражение для мгновенного U_ab можно получить проведя расчет эл. сх. любым известным методом.

По законам Кирхгофа сост. ур-ие для опр. неизв. токов в ветвях. I_ab = 0 – усл. равновесия. Соотн. сопр. плеч внешне получается таким же, как и для моста пост. тока.

Z₁Z₃ = Z₂Z₄ (1)

Комплексные вел. предст. 2 способами – алг. и показ. форме. Z = R + jX₁ = Z₁e ^j1.

Подст. в рав. 1 компл. сопр. в показ. форме., т.е. Z₁e^j1Z₃e^j3= Z₂e^j2Z₄e^j4.

Z₁Z₃e^j(1+3)= Z₂Z₄e^j(2+4) (2)

Z₁Z₃ = Z₂Z₄–ампл. усл. равновесия.

₁+₃ = ₂+₄ – фазовое усл. равновесия.

1)Пусть Z₁ = R₁, Z₂ = R₂.

Т.к. сопр. чисто активное, ₃ = ₄. Из последнего равенства следует, что реактивное вкл. в плечи 3 и 4 должны быть одинаковой природы: емкостной или индукционной.

2)Пусть Z₁ = R₁, Z₃ = R₃.

По усл. равновесия ₂ = -₄. В случае такого моста нагрузки должны быть разной природы: X_L и X_C.

Вопрос№36 Мост Вина для измерения пар-р катушки.

Рассм. эл.схемуL₃ = L_X – ? R₃ = R_X – ? Запишем условие равновесия моста в общем виде и подставим значение комплексных сопротивлений.

Z₁Z₃ = Z₂Z₄.R₁(R₃ + jwL₃) = R₂(R₄ + jwL₄).

R₁R₃ + jwR₁L₃ = R₂R₄ + jwR₂L₄.

Приравниваем действительные и мнимые части:

R₁R₃ = R₃R₄ => R_X = R₂R₄/R₁

R₁L₃ = R₂L₄ => L_X = R₂L₄/R₁

Вопрос №37. Мост Сотти (для определения характеристик конденсаторов с малымиактивными потерями).

Составим мост Сотти. С₃ = С_X – ? R₃ = R_X – ?

Запишем условие равновесия моста в общем виде и подставим значение комплексных сопротивлений.

Z₁Z₃ = Z₂Z₄.R₁(R₃ + 1/ jwС₃) = R₂(R₄ + 1/ jwС₄).

R₁R₃ + R₁/ jwC₃ = R₂R₄ + R₂/ jwC₄.

Приравниваем действительные и мнимые части:

R₁R₃ = R₃R₄ => R_X = R₂R₄/R₁

R₁/C₃ = R₂/C₄ => C_X = R₁C₄/R₂

Вопрос№38 Методы измерения синусоидальных сигналов.

Электрические сигналы (ток, напряжение) изм. по гармоническому закону:

u(t) = U₀ sin(wt + ₀)

Частота  -физич [Гц] [Гц] = с^-1, связана с циклич.(круговой) частотой w по ф-ле w = 2п,

[w]=рад/с.

Для изм. частоты исп. следующие методы:

1. Метод непоср. изм. частоты с помощью осциллографа.

а. с линейной разверткой

б. с синусоидальной разверткой

В случае а на гор. откл. пластины X от ГЛИН пост. напряжение, изм. во времени по лин. пилообразному закону.

Под возд. лин. нараст. напр. электронный луч перем. в гор. напр. с пост. скоростью. Исследуемое син. напр. неизвестной частоты w_X подается на верт. откл. пластины (Y). При одновременном воздействии на эл. луч исследуемого напр. и напр. развертки, на экр. осциллографа набл. реальная зависимость вх. напр. от времени. На осциллографе имеются ручки упр., связанные с калибраторами амплитуды и длительности (В/дел., с/дел.).

Из обозн. следует, что при том или ином положении рукоятки задается значение напр. или времени по координатной сетке экр. Гор. отр. соответствует некоторому временному процессу, измеряемому в миллисекундах или микросекундах. Верт. отр. задает значение одного из отр. синусоиды. По координатной сетке можно опр. период син. напр., а значит и частоту.

В случае б на гор. откл. пластины подается не пилообразное, а синусоидальное образцовое высокостабилизированное с частотой w₀ напр. (50 кГц)

Одновременно на Y-пластины подается исследуемый син. сигнал частотой w_x = 2пf_x. При выполнении условия кратности частот f_x/f₀ = n, f₀/f_x = m, где m и n – целые значения. Электронный луч под одновременным воздействием 2 син. напр. вычерчивает разнообразные кривые в зависимости от m и n, наз. фиг. Лиссажу. По характерному виду фигуры можно опр. значение кратности частот n и m, по к-рым опр. f_x.

Простейшая фиг. Лиссажу – эллипс, при m = n = 1. В зависимости от фазового сдвига между напряжениями U_X(t) и U_Y(t) эллипс вырождается в окружность, при фазовом сдвиге  = п/2 + 2пk. В прямую с полож. угл. коэф. при фазовом сдвиге 2пk. С отр. угл. коэф. при фазовом сдвиге п + 2пk. Данный метод огр., т.к. требует вып. усл. кратности частот, что не всегда возможно.

2. Метод светящихся меток на круговой развертке. Осн. на исп. обр. частоты, равной 50 кГц и спец. устр., встроенного в приемник-компаратор, связывающего модулятор ЭЛТ с выходом Z приемника. Круговая развертка возн. благодаря делению опорного сигнала с частотой на RC цепях. При этом ток частоты, f₀ протекающий через емкость C и сопр. R создает на них падение син. напр. одинаковой частоты f₀, со сдвигом по фазе –п/2.

Эти напряжения подаются на верт. и гор. откл. пластины и создают круговую развертку. Если на вход Z приемника-компаратора подается син. напр. f_x, то при выполнении условия кратности f_x/f₀ = n, где n – целое, на круговой развертке появятся светящиеся точки (метки), число которых зависит от показателя кратности. Метод достаточно точен и используется при построении градуировочных кривых генераторов переменной частоты при их поверке.

3. Резонансный метод. Исп. в т.н. резонансных частотомерах, которые работают, исп. явление эл. резонанса в колебательном контуре. При выполнении условия резонанса .

L и C могут перестраиваться в узких диапазонах, поэтому резонансные частотомеры не получили широкого применения и исп. при реш. узкого круга задач.

Вопрос№39 Электронно-счетный цифровой частотомер

Широко исп. ЭСЦЧ, поскольку позволяет находить неизвестную частоту в диапазоне от десятков Гц до сотен МГц.

ФУ – блок формирующего устройства, преобр. син. напр. в посл. коротких импульсов полож. полярности, с частотой следования f_x, равной частоте син. сигн. Устройство вырабатывает полож. импульс в момент перехода в 0 с «-» на «+».

ГВЧ – генератор высокой частоты, с кварцевой стабилизацией, вырабатывает импульсы частотой 1 МГц – частота собст. колебаний пластинки природного кварца.

ДЧ – делитель частоты – устройство имеющее 7 декад, которое позволяет проводить деление частоты генератора в 10ⁿ раз, где n = 1,2...7. Период кварцевого генератора 1 мкс. Деление частоты повт. импульсов может меняться от 1 мкс до 10 с.

БУ – блок управления, вырабатывает имп. полож. полярности, равной периоду следования импульсов с ДЧ.

ВС – временной селектор – эл. у-во, раб. в реж. ключа, которое пропускает импульсы с ФУ за время действия упр. импульса.

СИ – счетчик импульсов, производит подсчет имп., пропускаемых ВС.

ЦИ – цифровой индикатор, выводит значение частоты в соответствии с формулой f_x = N/T_сч., где N – число подсч. имп., T_сч. – время действия упр. имп.