Информатика Никитин

31

1. как изменятся программы последней задачи, если кроме функции

y = y(x) требуется одновременно с ней при тех же значениях x

просчитать и z = z( x; y ) ;

2. как изменятся программы последней задачи, если требуется

протабулировать функцию от x = b до x = a с шагом -h, то есть в порядке убывания x .

ЧАСТЬ 2

Во второй части нашего курса рассмотрим простейшие приемы работы на VBA с подпрограммами и массивами, связанные с инженерно-

математическими расчетами.

При составлении сложных программ очень часто в их различных частях приходится использовать одинаковую последовательность действий,

например, вычислять При составлении программ по

такому алгоритму приходится записывать одну и ту же группу операторов,

соответствующих каждому из повторяющихся фрагментов. Для более эффективного программирования подобных повторений в алгоритмических языках предназначены подпрограммы. Повторяемая группа операторов оформляется в виде отдельной программной единицы, которая записывается однократно, а в соответствующих местах основной программы (или подпрограмм) организуются обращения к ней.

Использование подпрограмм позволяет сложную задачу разбить на фрагменты, которые выполняют различные исполнители. Кроме того,

подпрограмма может рассмотриваться как самостоятельный модуль, который выполнен квалифицированными разработчиками и используется пользователями более низкой квалификации.

В VBA подпрограммы разделяются на процедуры – Sub и

подпрограммы-функции – Function . Кроме того, от первоначальных

32

версий BASIC сохранилась конструкция подпрограмм GoSub – Return ,

которая в настоящее время редко используется и в нашем курсе не рассматривается.

Любая процедура может содержать несколько входных параметров,

произвольное число операторов и несколько результатов ее выполнения.

Синтаксис процедуры в упрощенной форме имеет вид:

[ Private | Public ] Sub <имя процедуры> ( список ) < операторы >

End Sub

Здесь квадратные скобки указывают на необязательный параметр,

вертикальная черта – на варианты параметров, выбираемых пользователем.

Так, элемент описания Private указывает, что рассматриваемая процедура доступна только из программы и процедур только того модуля, в

котором она описана. Элемент описания Public указывает на то, что рассматриваемая процедура доступна для всех программ и процедур во всех модулях. В предлагаемых образцах программ мы будем использовать процедуры только с описанием Public .

Список формальных аргументов процедуры мы условно на начальном этапе изучения разделим на входные параметры – исходные данные и выходные – результаты счета. Входные параметры в списке мы будем описывать с ключевым словом ByVal и обязательным указанием типа.

Выходные же параметры в списке будем описывать с ключевым словом

ByRef и обязательным указанием типа. При таком способе описания входные параметры передаются в процедуру по значению: вначале в вызывающей программе вычисляются значения фактических аргументов и эти значения подставляются в процедуре вместо формальных. Входные параметры могут быть либо постоянными, либо именными постоянными,

либо переменными, либо выражениями. Выходные параметры, описанные с ключевым словом ByRef , передаются по адресам в электронной памяти

33

компьютера и должны быть только переменными. После их вычисления в процедуре их значения передаются в вызывающую программу. Отметим, что каждая переменная, которая используется в качестве выходного параметра процедуры с ключевым словом ByRef в вызывающей программе, должна быть описана в ней только в отдельном операторе описания. Вызов процедуры из вызывающей программы осуществляется с помощью оператора

Call < имя процедуры > ( фактические переменные )

Так вычисление логарифма по произвольному основанию и образец

обращения к процедуре его вычисления можно представить в следующей

программе

Private Sub Workbook_Open() Const a = 2, b = 4

Dim x As Single

Dim y As Single

Dim z As Single

Call Логарифм(a, b, x)

Call Логарифм(a + b, (a + b) ^ 5, y) Call Логарифм(10, 10000, z) Range("A1").Value = x Range("A3").Value = y Range("A5").Value = z

x = 2.38 ^ b y = 3.1415926

Call Логарифм(y, x, z) Range("A7").Value = z End Sub

Public Sub Логарифм(ByVal основание, аргумент _ As Single, ByRef результат _ As Single)

результат = Log(аргумент) / Log(основание) End Sub

34

Отметим, что одновременное использование латинского алфавита и кириллицы при написании программ на начальном этапе затруднительно. В

приведенном примере это сделано для большей наглядности.

Кроме того, что в процедуре может быть несколько выходных параметров, описанных с ключевым словом ByRef, возможны побочные результаты действия процедур на изменение входных параметров с ключевым словом ByVal – в предлагаемом курсе не рассматриваются.

Подпрограмма-функция – это подпрограмма, результат которой есть единственное значение, присваиваемое имени этой функции. Подпрограмма-

функция оформляется в следующем виде

[Public | Private] Function < имя функции >(список) _

As < тип >

< операторы > End Function

В местах выхода из подпрограммы-функции должен стоять оператор присваивания

< имя функции > = < выражение >

Обращения к подпрограммам-функциям аналогичны обращению к стандартным математическим функциям VBA.

Рассмотрим оформление предыдущего примера в виде подпрограммы-

функции и обращения к ней

Private Sub Workbook_Open() Const a = 2, b = 4

Dim x As Single

Dim y As Single

Dim z As Single

x = Логарифм(a, b)

y = Логарифм(a + b, (a + b) ^ 5) z = Логарифм(10, 10000) Range("A1").Value = x Range("A3").Value = y Range("A5").Value = z

35

x = 2.38 ^ b y = 3.1415926

z = Логарифм(y, x) Range("A7").Value = z End Sub

Public Function Логарифм(ByVal основание, аргумент _ As Single) As Single

Логарифм = Log(аргумент) / Log(основание) End Function

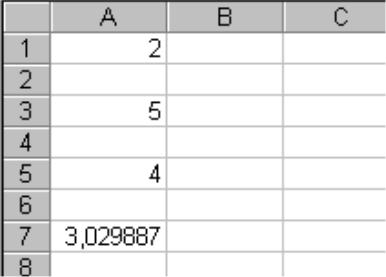
Результат счета по приведенным программам одинаковый и имеет вид:

Перейдем к изучению массивов. В предыдущей части программирования на VBA рассматривались переменные, являющимися только скалярными величинами. Однако при решении научно-технических и экономических задач приходится сталкиваться с совокупностью переменных,

объединенных одним именем, но с различными индексами. Простейшими примерами таких переменных являются элементы векторов и матриц.

Аналогом таких переменных в алгоритмических языках являются массивы. В

36

общем случае массив – это упорядоченное конечное множество элементов одинакового типа.

Если в математике, как правило, индекс указывается несколько ниже

имени переменной, например x 1 , x 2 , ..., x n или xi – для элементов векторов и a i j – для элементов матриц, то в VBA индексы заключаются в круглые

качестве индексов можно использовать переменные перечисляемого типа.

Например, названия дней недели, названия цветов радуги и так далее. Мы же будем рассматривать простейший случай, когда в качестве индексов используются аргументы целого типа с указанием пределов их изменения.

Число индексов в массиве определяет его размерность.

Для работы с массивами необходимо их предварительно описать. В

нашем курсе мы их будем описывать в операторах Dim с указанием границ изменения его индексов в виде граничных пар. При этом объявление

Здесь описаны три массива. Вектор a вещественного типа, состоящий

c(2,1) c(2,2) c(2,3) c(2,4)

Границы изменения индексов массивов можно описать либо в виде граничных пар чисел, как указано выше, либо в виде граничных пар именных констант. Например:

37

Следует отметить, что должно соблюдаться условие: m ≤ n . Если же m = n , то соответствующий индекс может принимать только одно значение.

Довольно часто массивы описываются с запасным количеством элементов, например вектор, состоящий из 100 элементов, а в программе используются только часть этого массива. Например, только 30 элементов массива.

В качестве индексов массивов в наших задачах могут быть использованы либо целые числа, либо целые именные постоянные, либо целые переменные, либо арифметические выражения целого типа. В VBA не определены операции над массивами. Поэтому всевозможные арифметические и математические действия с массивами проводятся с элементом массива, для которого указаны индексы (индекс). Обычно это производится с помощью операторов цикла, используя целочисленные параметры этих операторов.

Для использования массивов в подпрограммах часто используется их описание в виде динамических, для которых размерность и диапазон изменения параметров определяется вызывающей программой. Например, x(). Использование динамических массивов в качестве входных и выходных параметров подпрограмм допускается только с ключевым словом

ByRef и они обязательно должны быть описаны в конце списка

параметров подпрограммы . Если в подпрограмме используется несколько

массивов, то каждый из ник должен содержать в описании ключевое

слово ByRef и описание типа.

Студенту необходимо разобраться в приведенных образцах решения

задач контрольной работы № 2 и модифицировать программы согласно

условиям своего варианта.

6.Даны векторы a R16 и b R12 . Для каждого из них найти произведение абсолютных величин ненулевых элементов.

Задача 3

1.Из двух массивов a(9) и b(12) получить новый массив c , состоящий из неотрицательных элементов исходных массивов. Полученный массив расположить в порядке возрастания.