2.4.2. Проникновение пуль в преграду

Баллистические характеристики пороха.

1)Сила пороха F – работа , которую могут совершить образующиеся газообразные продукты при полном сгорании 1 кг пороха без участия кислорода воздуха.

Размерность силы пороха Дж/ кг.

2)Коволюм - объём газообразных продуктов горения, образующихся при сгорании в заданных условиях 1 кг пороха.

3)Удельная поверхность пороха – отношение общей поверхности зёрен заряда к его видимому объёму. Размерность м² /м³ .

Кроме баллистических характеристик пороха на величину и характер нарастания давления влияет плотность заряжания . Плотность заряжания представляет собой отношение массы порохового заряда к тому объёму, в котором происходит горение этого заряда.

Размерность – кг/ м³

При высокой плотности заряжания, характерной для пулевых перфораторов, пакеров, стреляющих грунтоносов и других устройств, используемых в глубоких скважинах, давление в каморе сгорания может достигать 2000 МПа.

Проникание пуль в преграду.

Пулевые перфораторы последнего поколения обеспечили высокую эффективность вторичного вскрытия в глубоких нефтяных скважинах. Скорость пули на выходе из ствола (дульная скорость) достигает сотен метров. С учётом большой массы пули в глубоких нефтяных скважинах гарантированно обеспечивается пробитие 1- 2 обсадных колонн, цементного камня и формирование в породе канала с сеткой трещин.

Глубина проникновения пули в полубесконечную преграду может быть определена путём совместного решения следующих уравнений :

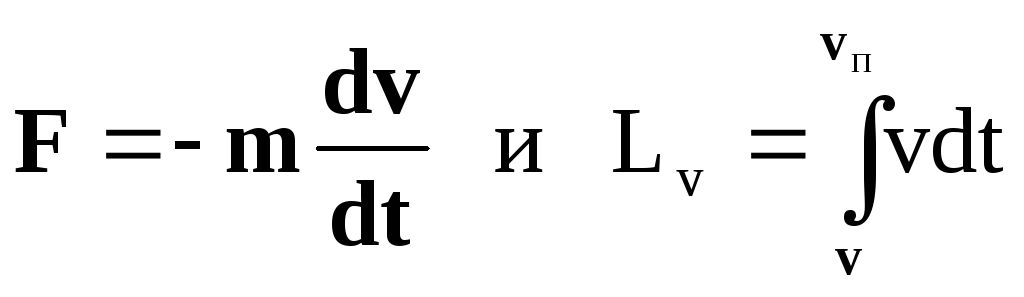, (2.20)

где :F–сила давления пули на преграду при скорости последней v;

m – масса пули; L_V - длина канала при текущей скорости v пули;

v_{п -} скорость входа пули в преграду.

Сила давления F сложным образом зависит от характеристик преграды. Лучшие результаты даёт полуэмпирическая закономерность связывающая силы сопротивления сплошной полубесконечной преграды и силу давления F пули на преграду при скорости последней v :

(2.21)

, (2.22)

Где s – площадь поперечного сечения пули;

-собственное прочностное сопротивление преграды, т.е. сопротивление разрушению или уплотнению материала преграды; bv² –инерционное сопротивление среды, обусловленное помимо прочего плотностью среды и формой головной части пули; k – коэффициент, зависящий от всего комплекса характеристик преграды и формы головной части пули.

Из (220) и (2.21) получаем уравнение движения пули в преграде

. (2.23)

После умножения левой и правой части уравнения на dL получим

dL (2.24)

dL.

Тогда дифференциал длины канала равен

dL = . (2.25)

Для получения длины канала при снижении скорости от v_с до v необходимо проинтегрировать dL в пределах от 0 до L_{V ,} а правую часть уравнения - от v_с до v:

L_V = (2.26)

Полная длина канала соответствует остановке пули, т.е.v = 0. При этом условии из (2.26) получаем

L_кп = (2.27)

Физический смысл и содержание параметров а и bv² следующие: a = H_п(v) мгновенное динамическое прочностное сопротивление преграды внедрению пули, зависящее от её скорости; bv² - гидродинамическое инерционное сопротивление преграды, равное , гдекоэффициент головной части пули; ρ_п -плотность материала преграды. Заменяя а и bv² в (2.27) на указанные значения, получим

L_кп = . (2.28)

Определим значения λ и H_{п ,} предварительно заменив m на произведение объёма пули на плотность её материала .

Коэффициент λ для пуль с коническим заострением может быть определён с использованием формулы Ньютона:

,

где α – половина угла заострения.

H_п (с – коэффициент, учитывающий рост динамического прочностного сопротивления преграды с ростом скорости пули -v_c; HB -динамическая твёрдость материала преграды по Бринеллю для металла) .При скоростях пули v_c ≈ 100 м /c коэффициент с равен 1,5

Формула (2.28) для полной длины канала в металлической преграде с плотностью ρ_мп, после подстановки в неё значений λ , H_п и с, приобретёт следующий вид:

L_кп =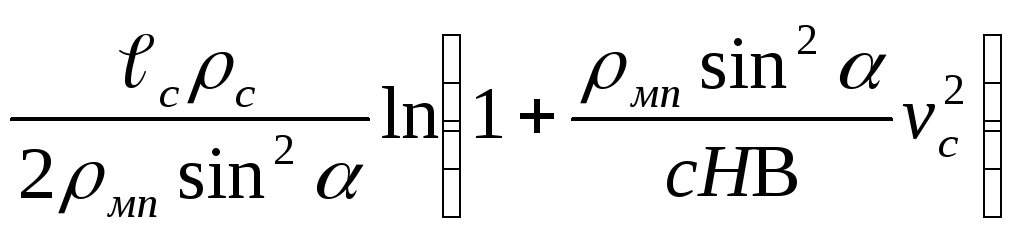. (2.29)

Для пород формула будет иметь аналогичный вид, но плотность преграды должна соответствовать плотности породы :

L_кп =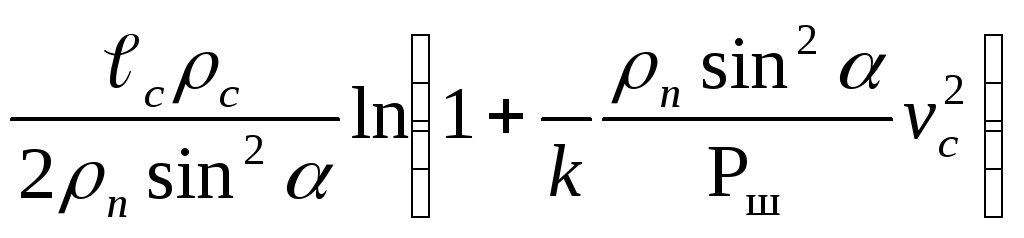, (2.30)

где Р_ш – твёрдость породы по штампу, k - коэффициент, учитывающий изменение динамического прочностного сопротивления породы при изменении скорости пули на входе в породу; его значение может быть получено опытным путём для определённых групп прочности пород.