3. Методики расчета температурных условий при горячей прокатке

3.1. Расчет температурных условий прокатки на непрерывных

широкополосных станах

Существуют два направления решения температурной задачи прокатки. Одно из них базируется на теоретических зависимостях процесса теплопередачи, другое — на статистическом анализе результатов экспериментальных исследований температур полос.

Явления теплообмена, сопутствующие процессу пластической деформации, весьма сложны. Поэтому при определении параметров теплообмена обычно принимают ряд упрощающих допущений, что позволяет использовать при анализе процесса теплопроводности феноменологический метод, основанный на установлении законов, определяющих рассматриваемое физическое явление в целом. Законы имеют весьма общий характер, а роль конкретной физической среды учитывается введением коэффициентов (коэффициент теплопроводности, коэффициент теплоотдачи, степень черноты и т. д.). Эти законы и коэффициенты пропорциональности устанавливаются опытом.

Феноменологический метод рассматривает изучаемую среду как сплошную, т. е. пренебрегает ее дискретным строением.

Теоретический анализ, основанный на феноменологическом методе, предусматривает составление уравнений суммарного теплового баланса.

Изменение температуры сляба-полосы во время прокатки и транспортировки происходит из-за потери тепла излучением и конвекцией, потери тепла вследствие соприкосновения полосы с рабочими валками и охлаждающей жидкостью и притока тепла вследствие превращения части энергии деформации металла в тепловую энергию.

Расчет теплового баланса без допущений затруднен, так как, во-первых, отсутствуют строгие математические зависимости, описывающие элементарные процессы теплопередачи и их взаимную обусловленность и, во-вторых, теоретическая модель должна отражать особенности технологии и

оборудования каждого конкретного стана. Не случайно все существующие модели температурных условий прокатки содержат корректирующие коэффициенты, значения которых не всегда научно аргументированы. В связи с этим широкое распространение получили эмпирические зависимости, построенные на основе данных экспериментального изучения изменения температур полос во время технологического процесса. Общая структура статистической модели должна базироваться на физической природе процесса теплопередачи и содержать в качестве аргументов основные параметры технологического процесса, легко поддающиеся измерению и регулированию (например, толщина полосы, скорость прокатки, абсолютное обжатие и т. д.). Основным недостатком статистических моделей является ограниченная область применения, так как эти модели отражают конкретную технологию и оборудование стана, для которого они рассчитывались. В то же время экспериментально-статистические модели процесса позволяют избежать усложнения алгоритма управления, что сокращает длительность подготовки и освоения АСУ и обеспечивает их высокую надежность. Перейдем к расчету основных статей суммарного теплового баланса.

1. Излучение. Для определения падения температуры вследствие излучения можно использовать уравнение:

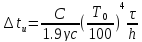
где с — средняя удельная теплоемкость полосы, кДж/(кг·°С);Т0 — температура начала охлаждения, К;γ — плотность прокатываемого металла, кг/м3;С — постоянная лучеиспускания охлаждаемой полосы, кДж/(м2·ч·°С);h — толщина полосы, мм; τ — продолжительность охлаждения, с.

При выводе этих уравнений приняты следующие допущения: 1) температурный градиент по толщине, ширине и длине полос отсутствует; 2) теплоизлучение верхней и нижней поверхностей одинаково; 3) теплоемкость, плотность и коэффициент излучения считаются постоянными величинами, не зависящими от температуры и окисленности излучающей поверхности.

Принятые допущения обусловили значительную погрешность (10—15 %)

2. Конвекция. Потери тепла за счет конвекции при прокатке на непрерывных станах точно определить трудно. Вследствие их небольшой величины в расчетах эти потери обычно оценивают в пределах 3—5 % от потерь тепла излучением. Расчет теплопотерь конвекцией показал, что их величина от падения температуры металла излучением составляет соответственно 10—18; 11—12; 16-22; 8—10 и 1—5 %.

3. Теплопередача соприкосновением. В методике, приведенной ниже, учтена потеря тепла за счет теплопроводности и при контакте прокатываемой полосы с рабочими валками. Процесс отдачи тепла воде, кипящей на поверхности полосы, изучен недостаточно. Потери тепла полосой из-за соприкосновения с валками можно найти по формуле:

где γ — плотность прокатываемого металла, кг/м3; С — постоянная

лучеиспускания прокатываемой полосы; τ — продолжительность

охлаждения, с; Т0 — температура начала охлаждения, К; Tвоз — температура

окружающего воздуха, К; 􀟯— коэффициент теплопередачи, кДж/(мм2·c·°С);

l3 — длина дуги захвата, мм; Vτ — объем металла, проходящий через очаг

деформации за единицу времени, мм3/с; b — ширина полосы, мм.

4. Выделение тепла в результате пластической деформации металла. Большинство исследователей рекомендуют не учитывать ту часть работыпластической деформации, которая расходуется на нагрев валков, нагрев поверхностных слоев полосы силами внешнего трения и превращается в потенциальную энергию искаженной решетки. Расчета повышения температуры металла вследствие его пластической деформации, вычисляется по формуле: