3.3. Уравнение Лапласа в полярных координатах

При решении многочисленных задач математической физики часто используется двумерное уравнение Лапласа

, 46)

решение, которого часто выгоднее искать в полярных координатах.

Преобразуем уравнение 46) к полярным координатам, положив

Дифференцируя по правилу дифференцирования сложной функции

, ,

но

, ,

а тогда

, ,

,

аналогично .

Теперь

, .

Применяя правило дифференцирования сложной функции к производным и, найдем вторые частные производные

,

аналогично

.

Теперь .

Таким образом, уравнение Лапласа в полярных координатах имеет вид

. 47)

3.4. Решение краевых задач методом разделения переменных

Решение краевых задач для уравнения Лапласа может быть найдено методом разделения переменных в случае некоторых простейших областей (прямоугольник, круг, сектор и др.). При решении конкретных задач обычно пользуются общим решением уравнения Лапласа, которое получается методом разделения переменных и имеет вид:

- в полярных координатах

; 48)

- в декартовых координатах

. 49)

Неопределенные коэффициенты иопределяются из граничных условий и физического смысла задачи.

1. Решение уравнения Лапласа в кольце

Найдем решение уравнения Лапласа в кольце, ограниченном окружностями ии принимающее следующие граничные значения

, , 50)

где ,- постоянные.

Для решения поставленной задачи воспользуемся соотношением 48). Удовлетворяя первому граничному условию из 50), получим

,

так как здесь левая часть не зависит от , то в правой следует положить. И теперь решение имеет вид

. 51)

Таким образом, удовлетворение граничным условиям 50) приводит к

следующей системе для отыскания неизвестных коэффициентов :

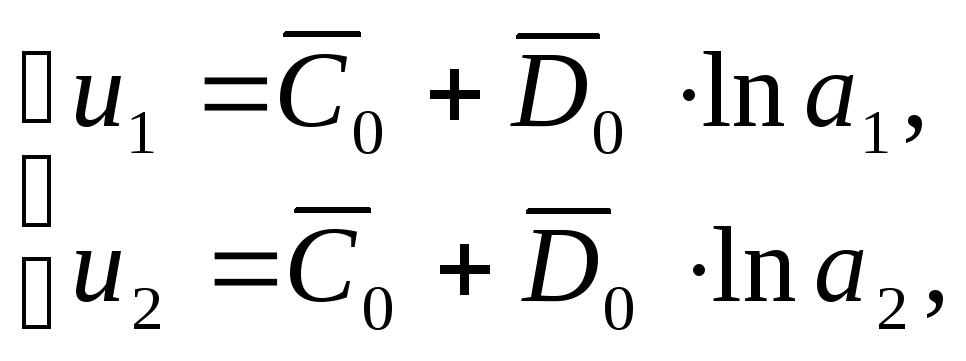
откуда находим

, .

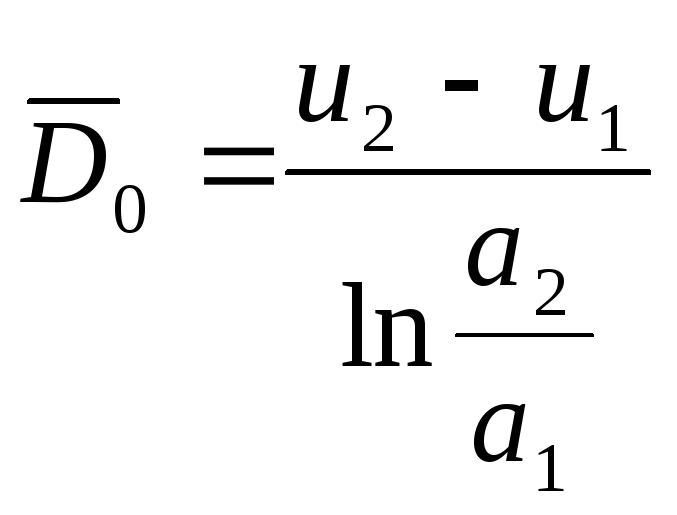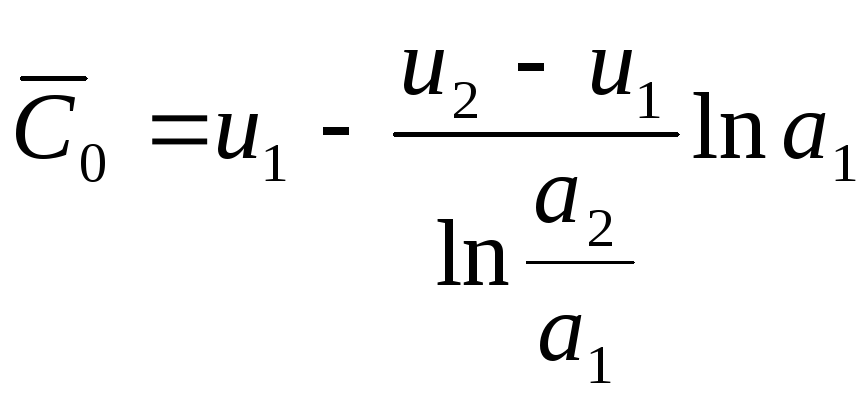Подставляя найденные значения ив формулу 51) окончательно получим решение сформулированной задачи для кольца:

.

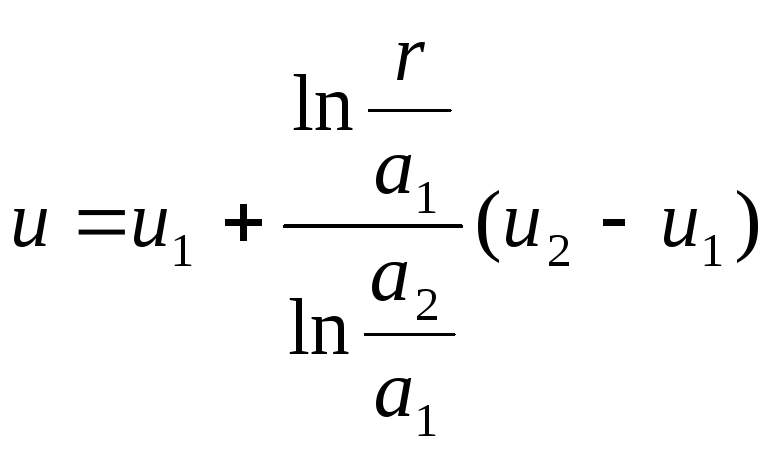2. Решение задачи Дирихле для полуполосы

Требуется найти решение уравнения Лапласа внутри полуполосы (), удовлетворяющее граничным условиям:

- ,;

- ,;

- ,,

где ,,- постоянные.

Для решения задачи воспользуемся соотношением 49). Решение задачи должно быть ограниченным при , поэтому в 49) следует положить:

,

здесь включено ви, а- ви.

Определим ,из первого граничного условия:

,

откуда ,, следовательно,

.

Из третьего граничного условия получаем:

,

откуда и, или,. Теперь искомое решение

. 52)

Коэффициенты определятся из второго граничного условия

,

или .

В последнем соотношении известная линейная функция, стоящая в левой части представлена (в правой части) в виде разложения в ряд Фурье по синусам кратных дуг на интервале .- коэффициенты Фурье этого разложения, они вычисляются по формулам

. 53)

Таким образом, сформулированная задача имеет решение 52) - 53).