2. Уравнение лапласа

К уравнениям эллиптического типа приводит изучение стационарных, т. е. не изменяющихся во времени, процессов различной физической природы. Сюда относятся стационарные электрические и магнитные процессы, потенциальное движение несжимаемой жидкости, стационарные тепловые процессы, собственные колебания стержней, мембран и т. д. Простейшим уравнением эллиптического типа является уравнение Лапласа: .

Функции, удовлетворяющие уравнению Лапласа, называются гармоничес-кими. В каждой конкретной задаче, приводящей к уравнению Лапласа, искомое решение выделяется из множества всех гармонических функций определенным дополнительным условием, которое называетсякраевымилиграничным. В отличие от волнового уравнения и уравнения теплопроводности задачи для эллиптических уравнений характеризуются отсутствием начальных условий. Краевые (граничные) условия задаются на границеГ области, в которой ищется решение дифференциального уравнения.

Задача здесь формулируется следующим образом. Требуется найти функцию , удовлетворяющую в некоторой области уравнению Лапласа, а на границе областиГ граничному условию, которое может быть взято в одном из следующих видов:

- наГ (задача Дирихле);

- наГ (задача Неймана).

Здесь ,- заданные функции, - производная по внешней нормали

к границе Г. Если решение ищется в области внутренней (внешней) по отношению к границеГ, то соответствующая задача называетсявнутренней(внешней) краевой задачей.

3.1. Стационарное температурное поле

При изучении уравнения теплопроводности было установлено, что температура нестационарного теплового поля удовлетворяет уравнению

.

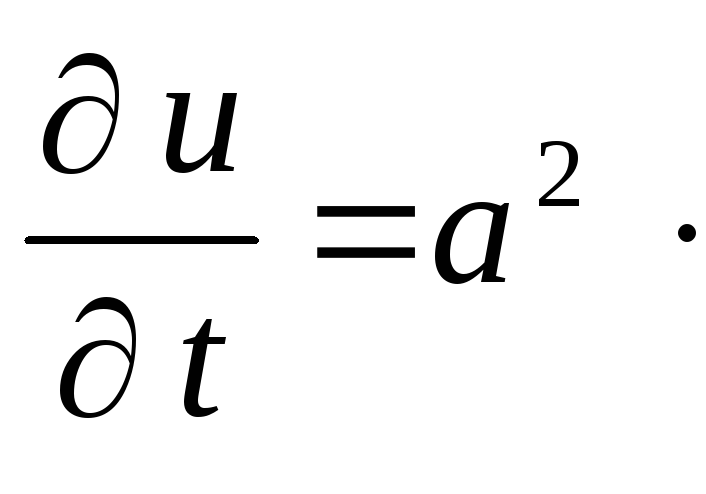
Если процесс стационарен, то и, таким образом, устанавливается распределение температуры, удовлетворяющее уравнению Лапласа.

Если требуется получить распределение температуры в некоторой области, ограниченной поверхностью Г, то к этому уравнению следует присоединить граничные условия:

- наГ (заданное распределение температуры на границе);

- наГ (заданный тепловой поток через границу).

3.2. Потенциальное течение жидкости

Рассмотрим движение идеальной жидкости, характеризующееся скоростью. Выделим в жидкости некоторую неподвижную замкнутую поверхностьпроизвольной формы (рис. 5) и рассмотрим массу жидкости, вытекающей за единицу времени из замкнутой поверхности.

Эта масса выражается поверхностным интегралом , где- плотность жидкости,- нормальная составляющая скорости. Истечение жидкости из замкнутой поверхностиповлечет за собой уменьшение плотности в точках внутриза единицу времени на величинуи соответствующее изменение массы жидкости внутри поверхности, равное, где- пространство, ограниченное поверхностью.

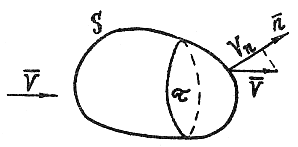
Рис. 5

Поскольку масса сохраняется, то

=,

преобразуя поверхностный интеграл по формуле Остроградского, получим

.

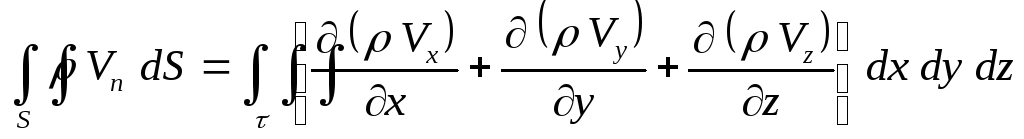Теперь

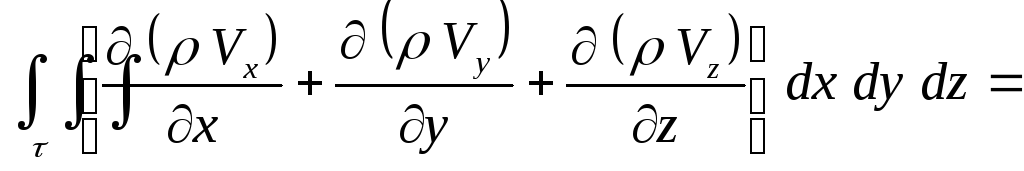
или

.

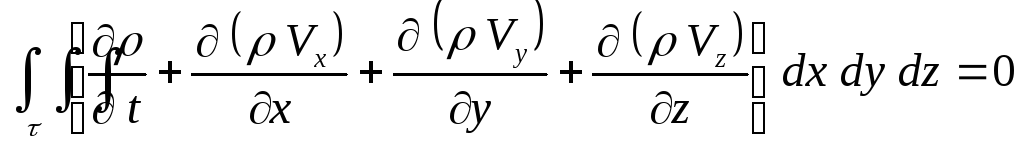Вследствие произвольности объема приходим к уравнению

,

которое называется уравнением неразрывности.

Если жидкость несжимаема () и движение стационарно, то уравнение неразрывности принимает вид

. 44)

Предположим, что движение жидкости потенциальное. Это значит, что скорость является градиентом некоторой функции

, 45)

называемой потенциаломскорости. Равенство 45) равносильно следующим трем,,. Таким образом, приходим к уравнению Лапласа.

Если жидкость обтекает границу Г, представляющую собой твердую непроницаемую стенку, то нормальная составляющая скорости равна нулю, что приводит к граничному условиюнаГ.

К уравнению Лапласа сводятся также многочисленные задачи теории упругости, электростатики, магнитостатики и др.