5. Решение первой краевой задачи для уравнения теплопроводности методом конечных разностей

Первая краевая задача для уравнения теплопроводности формулируется следующим образом. Требуется найти решение уравнения теплопроводности 3), удовлетворяющее краевым условиям:

, ;

, ; 39)

, .

Таким образом, требуется найти решение в прямоугольнике, ограниченном прямыми,,,, если заданы значения искомой функции на трех сторонах прямоугольника,,.

Одним из наиболее простых приближенных методов решения этой краевой задачи является сведение ее к системе конечно-разностных (сеточных) уравнений. Для этого покроем область решения сеткой, образованной прямыми ,, и будем определять приближенные значения решения в узлах сетки, то есть в точках пересечения этих прямых. Введем обозначения. На основании теоремы о конечных приращениях Лагранжа, заменим производные соответствующими разностями:

,

,

.

Теперь вместо дифференциального уравнения 24) имеем соответствующее ему уравнение в конечных разностях для точки

.

Определим из этого соотношения

. 40)

Из последней формулы видно, что по трем известным значениям искомой функции в j-том горизонтальном ряду,,определяется значениевi-ом горизонтальном ряду. Нам известны все значения температуры на прямой(из начального условия). По формуле 40) определяются значения температуры во всех внутренних точках отрезка(). Значения в крайних точках этого отрезка нам известны из граничных условий 39). Так ряд за рядом определяются значения искомого решения во всех узлах сетки.

Формула 40) упрощается, если шаг по осивыбрать так, чтобы было, тогдаи соотношение 40) принимает вид:. Последняя формула особенно удобна для вычислений. Доказывается, что, где- приближенное решение, полученное по последней формуле,- точное решение задачи.

2.6. Понятие пространственной задачи теплопроводности

Процесс распространения тепла в пространстве может быть охарактеризован температурой , являющейся функцией пространственных координат и времени. Среда, в которой распространяются процессы теплопередачи, характеризуется так называемымкалорическим уравнением состояния , плотностьюи коэффициентом теплопроводности. Здесь- внутренняя энергия тела, заключенная в единице массы, если эта масса нагрета до температуры.

Количество тепла, заключенное в бесконечно малом объеме, ограничивающем точку с координатами

, ,,

в момент времени равно. Изменение этого количества тепла за времябудет равно

.

Такое изменение может произойти только за счет того, что тепло вытекает или втекает через границу выделенного объема, если мы предполагаем, что выделения или поглощения энергии не происходит. Количество тепла (поток тепла), протекающего через площадку за время, равно

. 41)

Здесь - производная температуры по нормали к выделенной площадке. Тепло течет из области более высоких температур в область более низких. Формула 41) для потока тепла – закон теплопроводности Ньютона в изотропном теле, который является результатом систематизации большого количества опытных фактов.

Определим поток тепла через площадки, ограничивающие наш объем. Количество тепла, втекающее через площадку , равно

,

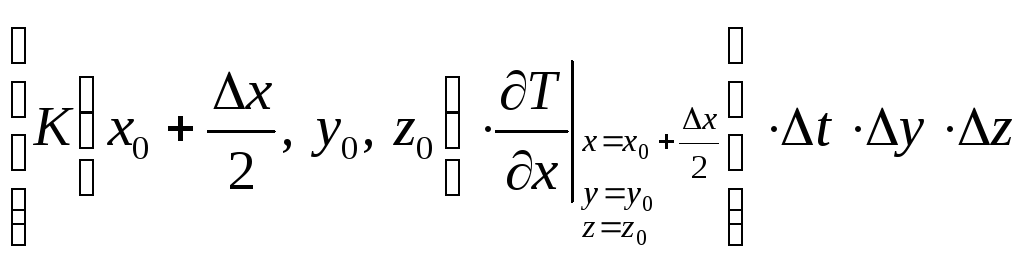а через площадку

.

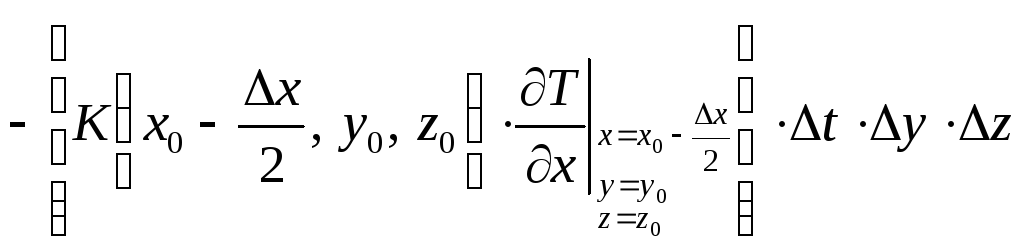Общее количество тепла, вошедшее в рассматриваемый объем через эти две площадки, будет

.

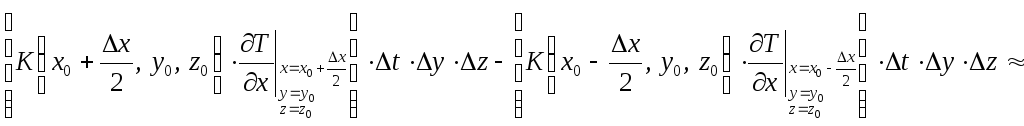
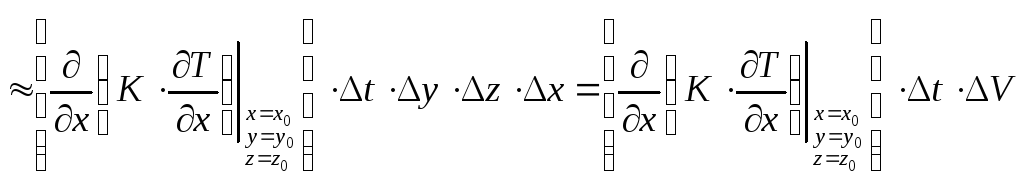Аналогично, количество тепла, вошедшее в рассматриваемый объем через площадки иза время, будет соответственно

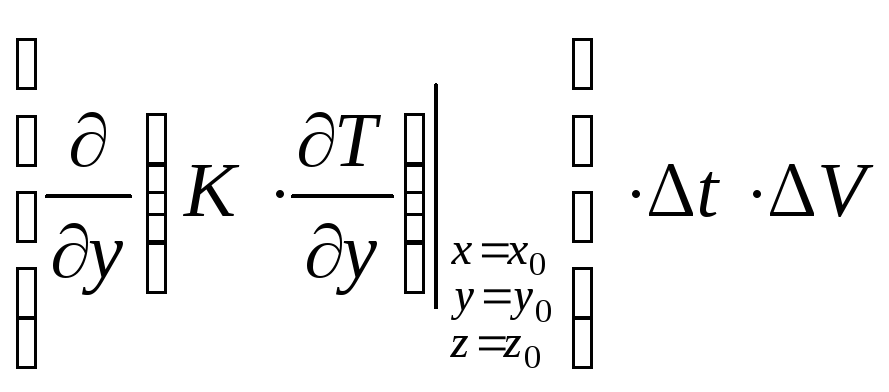и .

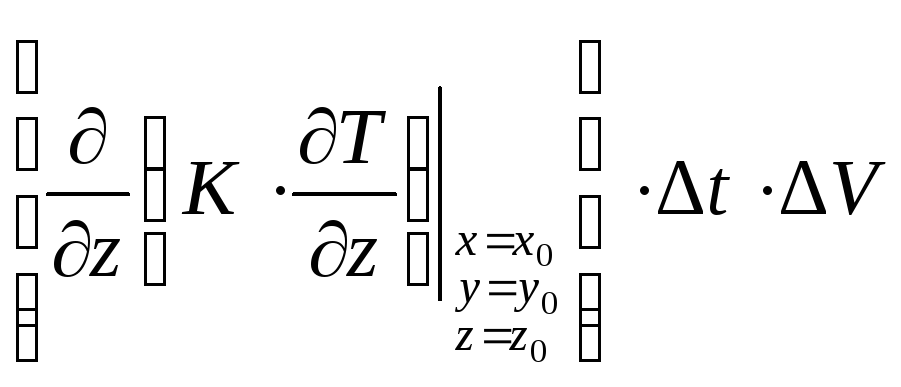Суммируя все полученные потоки тепла и, приравнивая их сумму изменению внутренней энергии, получаем

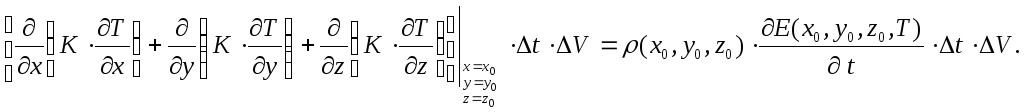Сокращая обе части последнего соотношения наи, замечая, что точкаможет быть выбрана произвольно (поэтому индекс ноль может быть опущен), приходим к окончательной форме уравнения теплопроводности

. 42)

В 42) , тогда. Обозначая- теплопроводность единицы объема, из 42) имеем

.

Если иявляются константами, тогда последнее соотношение примет вид. Коэффициентназывается коэффициентом температуропроводности. Из физических соображений он положителен. Обозначая его через, имеем следующий вид уравнения теплопроводности, где- оператор Лапласа. В двумерном случае оператор Лапласа -, в одномерном -. Если температура не зависит от времени- стационарное температурное поле, то распределение температуры определится из следующего уравнения Лапласа. 43)