2.3. Приведение задачи к однородным граничным условиям

Решить краевую задачу 24) – 27) методом разделения переменных Фурье невозможно, так как граничные условия 26), 27) неоднородны (им не удовлетворяет функция ). Поэтому, прежде чем применять метод Фурье, мы должны свести задачу к задаче соднородными граничными условиями. Выполним такое сведение для случая, когда температуры внешних средипостоянны.

Введем новую функцию , связанную сформулой

, 28)

где и- константы, которые подбираются так, чтобы для функцииполучались однородные граничные условия.

Подставляя по 28) в дифференциальное уравнение 24), получим дифференциальное уравнение относительно вспомогательной функции:

. 29)

Граничные условия 26) и 27) при подстановке 28) преобразуются следующим образом:

,

.

Требование однородности граничных условий для функции будет выполнено, если приравнять нулю квадратные скобки в правых частях последних соотношений, тогда

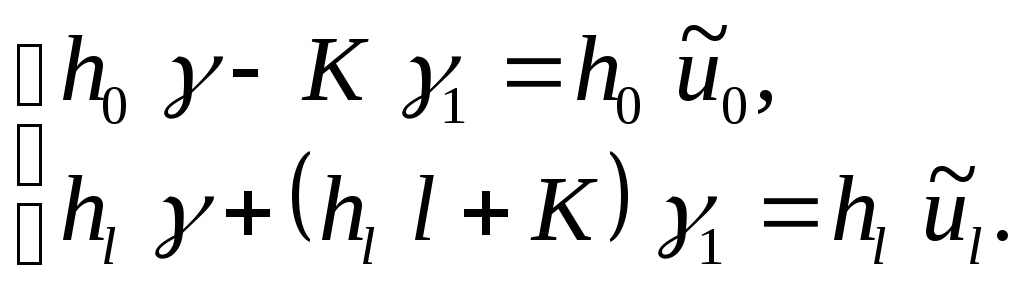30)

Из последней системы определятся коэффициенты и.

Теперь однородные граничные условия для :

, . 31)

Условие 25) преобразуется в начальное условие для следующим образом:. Поскольку константыик этому моменту вполне определенные числа из 30), то начальное условие дляимеет вид:

, 32)

где - определенная функция.

Теперь краевая задача 29), 31), 32) относительно – краевая задача с однородными граничными условиями (условиям 31) удовлетворяет) и может быть решена методом разделения переменных.

2.4. Решение краевой задачи для уравнения теплопроводности методом Фурье

В соответствии с методом разделения переменных, ищем решение уравнения 29) в виде произведения двух функций: . Тогда подстановкав таком виде в уравнение 29), дастили.

Приравниваем левую и правую часть последнего соотношения константе

.

Последние соотношения распадаются на два самостоятельных обыкновенных дифференциальных уравнения

и

или

и . 33)

Первое уравнение из 33) – обыкновенное дифференциальное уравнение первого порядка с разделяющимися переменными. Его решение

.

Поскольку ни в одном сечении стержня температура , а, следовательно, и функцияне может неограниченно возрастать по абсолютной величине при, тодолжно быть отрицательным. Обозначим. Тогда.

Второе уравнение из 33) теперь имеет вид . Это - однородное линейное уравнение второго порядка с постоянными коэффициентами. Его решение, строящееся по виду корней характеристического уравнения:.

Теперь решение задачи с однородными граничными условиями имеет вид , 34)

где ,- произвольные постоянные (неопределенные коэффициенты).

Реализуя в 34) граничные условия 31), получим

,

,

из этих соотношений имеем

и

откуда

.

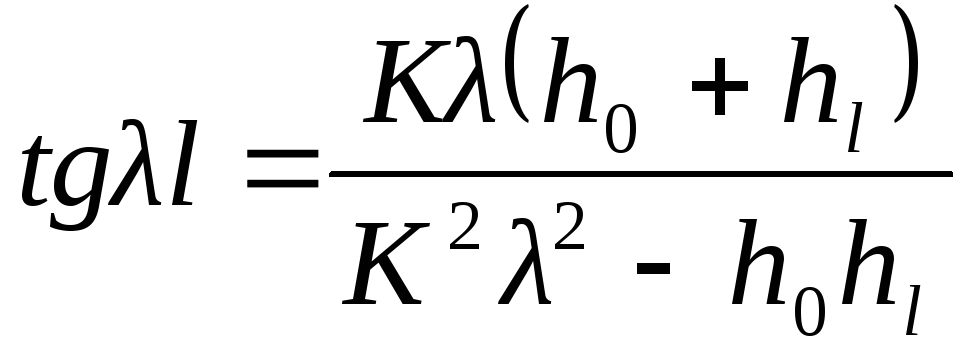Таким образом, успешность решения сформулированной краевой задачи 29), 31), 32) зависит от успешности решения последнего трансцендентного уравнения относительно неизвестной величины .

Рассмотрим дальнейшее решение поставленной задачи на следующем примере. Пусть исходная краевая задача, состоящая из дифференциального уравнения 24) и начального условия 25), имеет граничные условия такие, что левый конец теплоизолирован, а правый поддерживается при постоянной температуре:

, . 35)

Граничные условия 35) неоднородны и замена 28) приводит к следующей краевой задаче относительно введенной дополнительной функции :

,

, 36)

, .

Введенные константы иопределяются из системы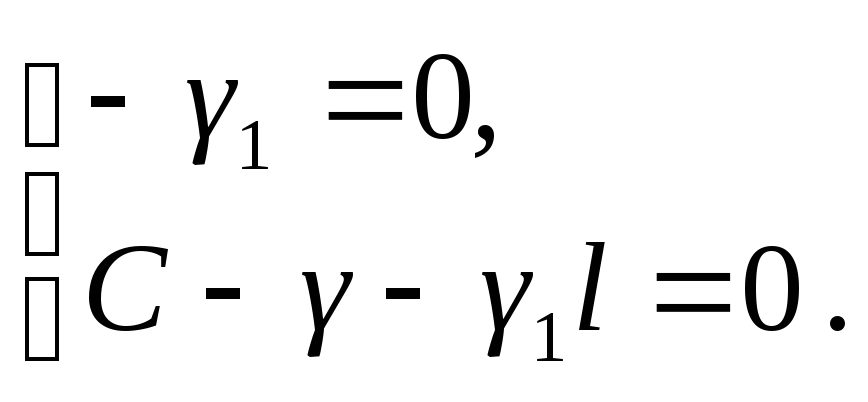

И равны и.

Решение методом разделения переменных дифференциального уравнения в 36) приводит к соотношению:

.

Реализация в последнем соотношении граничных условий из 36) дает

,

, - собственные числа решаемой задачи, функции- собственные функции.

Теперь частные решения .

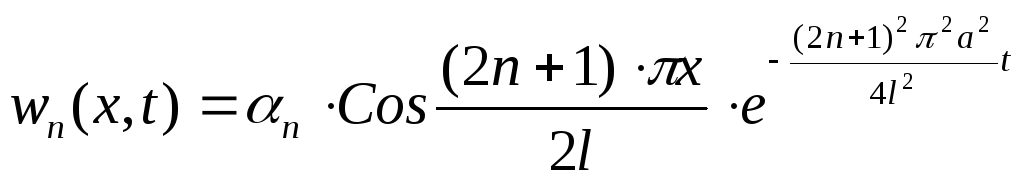Общее решение

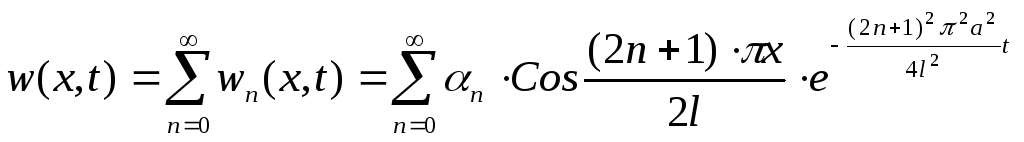. 37)

Коэффициенты определяются из начального условия, а тогда. Подчеркнутое выражение представляет разложение заданной функциив ряд Фурье по косинусам на интервале, коэффициенты этого разложения- коэффициенты Фурье, которые определяются по формулам:

. 38)

Таким образом, сформулированная краевая задача 36) имеет решение 37), где коэффициенты определяются по формулам 38).

Если начальная температура стержня постоянна , тои, а тогдаи теперь искомое решение имеет вид:

.

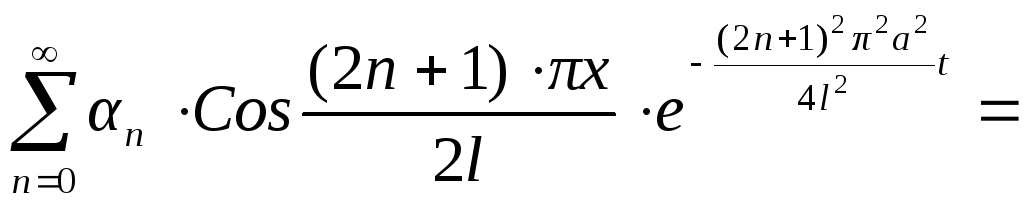
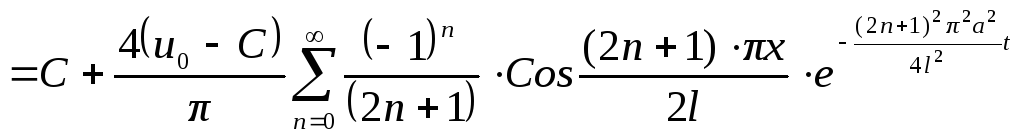Для качественного анализа полученного результата, ограничимся в ряде разложения для одним членом ряда, тогда

.

На рис. 3 приводится характер изменения температуры в стержне с ростом времени (кривые 1, 2, 3). Кривая 3 здесь соответствует более позднему моменту времени, чем кривые 1 и 2. Здесь принято .

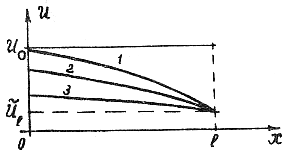
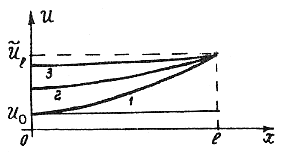
Рис. 3 Рис. 4

Если , то характер изменения температуры с ростом времени представлен на рис. 4. Кривая 3 здесь так же соответствует более позднему моменту времени, чем кривые 1 и 2. Таким образом, в нашем случае, когда стержень теплоизолирован с боков и со стороны левого торца, а правый то-рец поддерживается при постоянной температуре, температура в стержне с течением времени стремится сравняться с температурой правого торца.