2. Уравнение теплопроводности

2.1. Уравнение распространения тепла в стержне

Рассматривается однородный стержень длины , теплоизолированный с боков и настолько тонкий, что в любой момент времени температуру во всех точках поперечного сечения можно считать одинаковой. Расположим ось стержня вдоль осимежду точкамии(рис. 2). Пусть- температура в сечении стержня с абсциссойв момент времени.

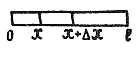
Рис. 2

Количество тепла, протекающего через сечение с абсциссой за время, определяется формулой

, 22)

где - площадь сечения стержня,- коэффициент теплопроводности материала стержня. Тепло течет из области более высоких температур в область более низких температур. Формула 22) для потока тепла получена опытным путем. Потоки тепла через сечения, ограничивающие элемент стержня, будут соответственно

и .

Приток тепла в элемент стержня за время будет

.

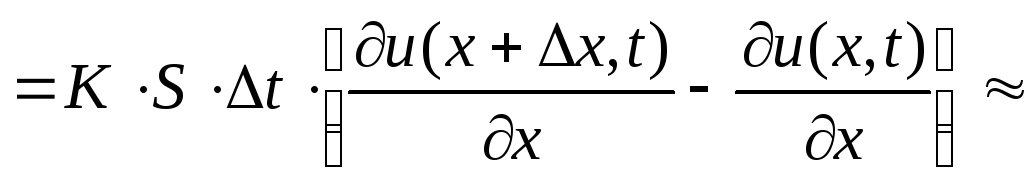
Этот поток тепла за время затратился на повышение температуры элемента стержня на величину:

, 23)

где - теплоемкость,- плотность вещества стержня.

Приравнивая правые части выражений 22) и 23), получим

или .

Из физических соображений , тогда.

Получаем окончательно:

. 24)

24) – уравнение распространения тепла (уравнение теплопроводности) в однородном стержне.

2.2. Постановка краевых задач

Чтобы решение уравнения 24) было определенным, к этому уравнению необходимо добавить краевые условия, состоящие из начального и граничных условий. Начальное условие задает температуру стержня в начальный момент времени

. 25)

Граничные условия могут быть различны в зависимости от температурного режима на торцах стержня. Наиболее общий случай граничных условий задает линейное соотношение между искомой функцией и ее производной. На левом конце стержня такое соотношение имеет вид:

. 26)

На правом конце стержня

. 27)

В формулах 26) , 27) и- коэффициенты теплообмена с внешней средой соответственно на левом и правом концах стержня;и- заданные температуры внешней среды соответственно у левого и правого торцов стержня, которые являются известными функциями времени, а в частном случае постоянные величины.

Частные случаи условий 26), 27) могут быть разными. Так, если левый конец стержня теплоизолирован, то коэффициент теплообмена равен нулю и условие тепловой изоляции из 26) имеет вид. В других случаях из 26) имеем и при очень больших значениях коэффициентов теплообмена(при) из 26) имеемили. Граничные условия на концахимогут быть различных типов и число различных краевых задач велико.