Уравнения математической физики

Изучаются дифференциальные уравнения в частных производных, т.е. уравнения, содержащие неизвестную функцию нескольких переменных и ее частные производные по этим переменным.

Порядок дифференциального уравнения – наивысший порядок частной производной, входящей в это уравнение. Например:

- уравнение первого порядка,

- уравнение второго порядка,

Уравнения математической физики– дифференциальные уравнения в частных производных второго порядка, линейные относительно неизвестной функции и частных производных от нее. Эти уравнения имеют широкое применение в физике, механике, технике.

Свойства дифференциальных уравнений в частных производных существенно отличаются от свойств обыкновенных дифференциальных уравнений. Так в отличие от обыкновенных дифференциальных уравнений, общие решения которых содержат произвольные постоянные, общие решения дифференциальных уравнений в частных производных могут содержать произвольные функции. Например:

имеет общее решение , поскольку при подстановке в уравнение удовлетворяет ему.

имеет общее решение .

Уравнения математической физики для функции двух переменных имеют общий вид:

, 1)

где - определенные постоянные числа,- заданная функция. Уравнение 1) принадлежит кгиперболическому типу уравнений, если, кпараболическомутипу, еслии к эллиптическомутипу, если. Если в уравнении 1) правая часть равна нулю, то уравнение называетсяоднородным. Оно имеет вид

. 2)

Решения однородных линейных уравнений обладают тем свойством, что если функции являются решениями уравнения 2), то их линейная комбинация, также является решением этого уравнения. Аналогичное свойство имеет

место для обыкновенных однородных линейных дифференциальных уравнений, однако, обыкновенное линейное дифференциальное уравнение n–го

порядка имеет в точности n линейно независимых частных решений, линейная комбинация которых дает частное решение. Уравнение же в частных производных может иметь бесчисленное множество линейно независимых частных решений, а тогда получаем общее решение дифференциальных уравнений математической физики в виде бесконечных рядов, членами которых служат произведения произвольных постоянных на частные решения:.

1. Волновое уравнение

1.1. Вывод уравнения колебания струны

Пусть имеется гибкая упругая струна. Гибкость струны означает, что напряжение в ней может быть направлено только вдоль струны. Упругость струны означает, что процесс деформации струны обратим, и при нем не происходит потери энергии. Струна тонкая, т. е. ее поперечные размеры пренебрежимо малы по сравнению с ее длиной равной . В состоянии равновесия струна прямолинейна и расположена вдоль осиOX между точкамии.

Если, закрепив концы струны, вывести ее из состояния равновесия, подвергнув действию какой-либо силы, то струна начнет колебаться. Будем считать, что движение всей струны происходит в одной плоскости и что каждая точка движется перпендикулярно оси OX. Смещение точки струны с координатойxв момент времениt будем обозначать. Все деформации струны малы, т. е. малы как смещения каждой точки струны, так и углы поворотов элементов струны.

Рассмотрим элемент струны (рис.1) , который в положении равновесия имеет концами точки x и. Пусть в результате отклонения струны в некоторый момент времени этот элемент переходит в положение. При этом, в силу малости деформаций, длина дугиприближенно равна. На концах деформированного элемента струны действуют силы натяженияв направлении касательных к элементу струны.

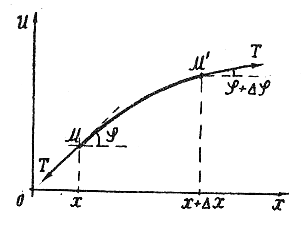
Рис. 1

Обозначим углы, образуемые этими касательными с осью OX, черези. Тогда вертикальная составляющая равнодействующей сил натяжения будет. Ввиду малости углов синусы можно заменить тангенсами, которые, в свою очередь равны производным:

.

Приравняем правую часть последнего соотношения силе инерции действующей на элемент , которая равна, где- линейная плотность материала струны. Тогда. Деля обе части последнего соотношения на, в левой части, в соответствии с теоремой конечных приращений Лагранжа, получим вторую производную отuпоxи теперь будем иметь. Посколькуи- положительные величины, то, обозначая, получим окончательно:

. (3)

(3) – уравнение свободных колебаний струны. Это уравнение описывает всевозможные колебательные (волновые) процессы и поэтому называется волновым уравнением.