4. Решение задачи Дирихле методом конечных разностей

Пусть требуется найти решение уравнения Лапласа

в плоской замкнутой области с границейГ (рис. 6), удовлетворяющее граничному условию

на Г,

где - заданная непрерывная функция.

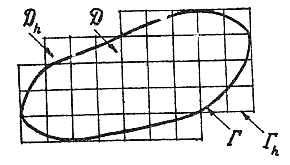
Рис. 6

Для решения сформулированной задачи проведем два семейства прямых

, ;,,

где - заданное число. Будем говорить, что областьпокрыта сеткой. Приближенное значение искомой функции в точкеобозначим. Аппроксимируем заданную областьсетчатой областью, состоящей из всех квадратов, целиком лежащих в областии некоторых пересекаемых границейГ. При этом контурГаппроксимируется контуромГ . В каждом узле, лежащем на контуреГ , зададим значение, равное значению функциив ближайшей точке контураГ. Значения искомой функции будем рассматривать только в узлах сетки. Заменим производные, входящие в уравнение Лапласа, конечными разностями:

, .

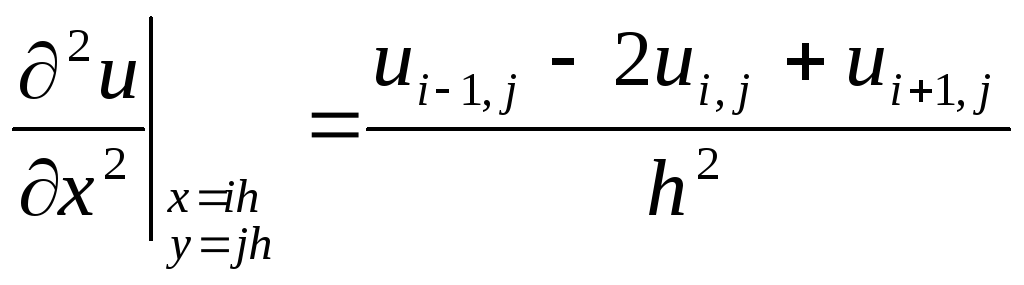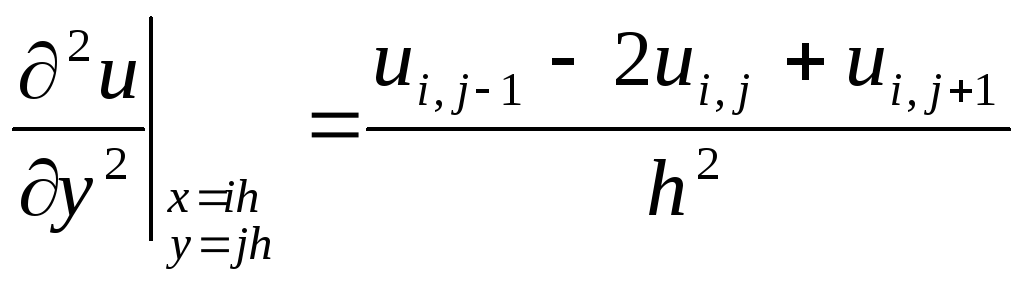Уравнение Лапласа заменится следующим уравнением в конечных разностях , или, сокращая наи разрешая относительно, получим:

. 54)

Уравнения 54) составляются для каждого узла сетки, лежащего внутри области и не лежащего на границеГ. Если точкасоседняя с точкой контураГ, то в правой части 54) будут известные значения.

Таким образом, получаем неоднородную систему N уравнений сNнеизвестными, гдеN – число узлов сетки, лежащих внутри области. Доказывается, что полученная система имеет решение и притом единственное. Определенные из системы 54) значения- приближенные решения сформулированной задачи Дирихле в точках построенной сетки.

ЗАКЛЮЧЕНИЕ

Уравнения математической физики отражают общие черты, свойственные тем или иным процессам. Особенности конкретного процесса устанавливаются условиями однозначности, которые состоят из геометрических, физических, временных и граничных условий. Геометрические условия содержат информацию о форме и размерах тела. Физические условия дают значения физических величин участвующих в процессе. Временные и граничные условия, объединяемые под общим названием краевых условий, указывают на особенности протекания процесса во времени и на границах тела. Математически сформулированная задача содержит дифференциальное уравнение и краевые условия.

Среди различных способов решения уравнений математической физики можно выделить аналитические, численные, графические и решение с помощью аналогов. С бурным развитием вычислительной техники последние два способа (графические и с помощью аналогов) стали иметь меньшее применение. Аналитические методы можно разделить на точные и приближенные. Для решения задач часто применяются метод разделения переменных и операционный способ. Из приближенных аналитических методов следует отметить интегральный и вариационные методы. Наиболее ценными методами численного решения таких уравнений является метод конечных разностей (метод сеток) и метод конечного элемента, которые позволяют найти решение в отдельных точках области искомого решения.

ЛИТЕРАТУРА

1. Численные методы решения физических задач : учеб. пособие / В. И. Ращиков, А. С. Рошаль. - СПб. ; М. ; Краснодар : Лань, 2005. - 208 с.

2. Поршнев С. В. Вычислительная математика. Курс лекций: Учеб. пособие / С. В. Поршнев. - СПб. : БХВ-Петербург, 2004. - 320 с.

3. Губенков А. А. Методы конечных и граничных элементов. Теоретические основы математического моделирования твердотельных упругих устройств / А.А. Губенков; Сарат. гос. техн. ун-т ; Сарат. гос. техн. ун-т (Саратов) . - Саратов : СГТУ, 2006. - 167 с.

4. Колокольцев В. А. Основы применения метода конечных элементов в расчетах деталей машин: учеб. пособие по курсу "Детали машин"для студ. машиностроит. спец. / В. А. Колокольцев ; Сарат. гос. техн. ун-т (Саратов). - Саратов : СГТУ, 2003. - 84 с.

5. Бочкарев А.В. Уравнения эллиптического типа и специальные функции: Учеб.пособие / А.В. Бочкарев, П.Б. Федоров. - Саратов: СГТУ, 2008. - 72 с.

6. Емельянов В. М. Уравнения математической физики : практикум по решению задач: Учеб. пособие / В. М. Емельянов, Е. А. Рыбакина. - СПб.; М.; Краснодар: Лань, 2008. - 224 с.

7. Сабитов К. Б. Уравнения математической физики: Учеб. пособие / К. Б. Сабитов. - М.: Высшая школа, 2003. - 255 с.

8. Тихонов А.Н. Уравнения математической физики: Учеб. пособие / А.Н. Тихонов, А.А. Самарский. – М.: МГУ, 2007. – 798 с.

9. Арсенин В.Я. Методы математической физики и специальные функции: Учеб.пособие / В. Я. Арсенин. - 2-е изд., перераб.и доп. - М. : Наука, 1984. - 384 с.

10. Годунов С. К. Уравнения математической физики: Учеб.пособие / С. К. Годунов. - 2-е изд., исправл. и дополн. - М. : Наука, 1979. - 392 с.

11. Владимиров В.С. Уравнения математической физики : Учебник / В. С. Владимиров. - 5-е изд., доп. - М. : Наука, 1988. - 512 с.

12. Бидасюк Ю.М. MathsoftMathCAD11: Самоучитель / Ю. М. Бидасюк. - М.; СПб.; Киев : Диалектика, 2004. - 224 с.

13. Глушаков С.В. Математическое моделирование: Mathcad 2000. Matlab 5; учебный курс / С. В. Глушаков, И. А. Жакин, Т. С. Хачиров. - Москва : АСТ ; Харьков : Фолио, 2001. - 524 с.

14. Дьяконов В. Mathcad 8/2000: Спец.справочник / В. Дьяконов. - СПб. : Питер, 2001. - 592 с.

15. Линьков В.М. Высшая математика в примерах и задачах. Компьютерный практикум: учеб. пособие / В. М. Линьков, Н. Н. Яремко ; ред. А. А. Емельянов. - М. : Финансы и статистика, 2006. - 320 с.

16. Мэтьюз Д.Г. Численные методы. Использование MATLAB / Д. Г. Мэтьюз, К. Д. Финк ; пер. с англ. под ред. Ю. В. Козаченко. - 3-е изд. - М., СПб., К. : Изд. дом "Вильямс", 2001. - 720 с.

17. Потемкин В.Г. Введение в MATLAB: Учебно-справочное изд. / В. Г. Потемкин. - М. : Диалог-МИФИ, 2000. - 247 с.

18. Третьяков С.А. Некоторые численные методы прикладной электродинамики : учеб. пособие / С.А. Третьяков, А.С. Черепанов, Ю.Н. Новиков. - СПб. : СПбГТУ, 1993. - 64 с.

19. Черняк А. А. Высшая математика на базе Mathcad. Общий курс: учеб. пособие / А.А. Черняк, Ж.А. Черняк, Ю.А. Доманова. - СПб. : БХВ-Петербург, 2004. - 608 с.

20. Вельмисов П. А. Уравнения математической физики: Учеб. пособие для студ. всех спец. техн. вузов / П.А. Вельмисов. - Ульяновск : УлПИ, 1994. - 75 с.

25