
Дополнение.
В задачах ( 6) и ( 7) были рассмотрены физические явления при применении к которым метода анализа размерностей число аргументов в функции больше трех; при этом число уравнений остается равным трем и система становится неопределенной.
В некоторых случаях может быть полезен следующий прием, предложенный автором: в число аргументов включается размерный параметр, представляющий собой отношение двух величин, отражающих действие разных сил в данном явлении. Очевидно, что цель этого- превратить два аргумента в один- в их отношение.
Заметим, что применение этого способа требует некоторого опыта.
В качестве примера, когда число неизвестных больше, чем число уравнений, рассмотрим задачу о определении зависимости для высоты h подъема воды в открытой стеклянной трубке, опущенной в жидкость.
Решение. Предварительно устанавливается следующий вид общей зависимости для высоты подъема:
![]()
в правую часть входит величина σ (коэффициент поверхностного натяжения жидкости), имеющая размерность [mt-2] и поэтому содержащая массу. Так как в левую часть масса не входит, то в аргументы правой части для исключения массы необходимо поместить величину, содержащую массу; самым простым аргументом в этом случае является плотность ρ. Такой путь рассуждений очевиден и часто применяется (особенно часто по отношению к массе). То же самое можно сказать о времени t: в σ входит время, а в левую часть оно не входит и для исключения его необходимо в аргументы правой части поместить простой аргумент, содержащий время- часто этим аргументом является g- ускорение свободного падения.
Общая зависимость для h с учетом плотности ρ и ускорения g принимает вид:
![]() (8)
(8)
Дальнейшие формальные действия приводят к равенству следующего вида:
![]()
или, после приравнивания степеней у одноименных первичных величин:

В результате получилась система трех уравнений с 4-мя неизвестными и дальнейшее решение задачи в этом направлении бессмысленно.
Для иного способа решения необходимо сформулировать из четырех аргументов в (8) в три путем комбинирования каких либо двух в один.
Сразу становится ясно, что комбинированным параметром не может служить отношение σ/ρ, т.к. масса сокращается и по m уравнения не составляются- по этому уравнений становится два, а неизвестных параметров остается три:
![]()
![]()
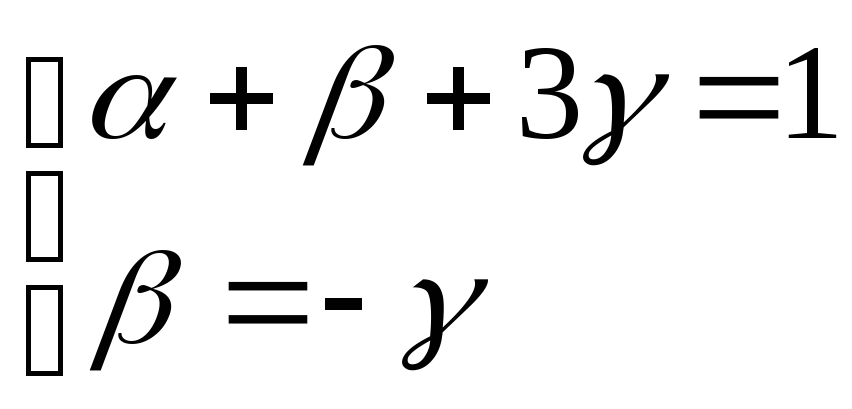
Следующим рассматривается параметр σ/r; тогда:
![]()
Система уравнений имеет вид:
 решение будет
таким
решение будет
таким
![]()
и функциональная зависимость (8) имеет вид:
![]()
Из приведенного анализа следует, что в случаях, когда неизвестных больше, чем уравнений необходимо подбирать комбинированные параметры, пригодность которых оценивается исходя из физического смысла явления.
