
Umk_Oed
.pdf
ρˆ coˆv( X ,Y ) ,
Sx S y
а оценками двух коэффициентов регрессии:
ˆ |
ˆ |
xy ρˆSx / Sy , |
yx ρˆS y / Sx . |
Все приведенные оценки будут так же и состоятельными, т.е. при n→∞ сходятся по вероятности к соответствующим теоретическим характеристикам.
Рассмотрим теперь m – мерную случайную величину
(Х1 , Х2 , …, Хm ). Пусть над системой произведено n независимых наблюдений и результаты оформлены в виде таблицы.
Табл. 3.8
i |
X1 |
X2 |
|
Xk |
|
Xm |
1 |
х1 1 |
х2 1 |
|
хk 1 |
|
хm 1 |
2 |
х1 2 |
х2 2 |
|
хk 2 |
|
хm 2 |
|
|
|
|
|
|
|
i |
х1 i |
х2 i |
|
хk i |
|
хm i |
|
|
|
|
|
|
|
n |
х1 n |
х2 n |
|
хk n |
|
хm n |
Здесь хk i – это значение, принятое компонентой вектора Xk в i-ом наблюдении.
Требуется найти оценки для числовых характеристик m − мерной
случайной величины: математических ожиданий |
mx , |
mx |
, …, |
mx |
, и |
||||||
|
|
|
|
|
|
|
1 |
|
2 |
|
m |
элементов ковариационной матрицы |
|
|
|
|
|
||||||
|
|
σ |
σ |
σ |
|
|
|
|
|
|
|
|
|
11 |
12 |
1m |
|
|
|
|
|
|
|
|
|
|
σ22 |
σ2m |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
σmm |
|
|
|
|
|
|
|
По главной диагонали ковариационной матрицы стоят дисперсии |
|||||||||||
компонент |
Х1 , Х2 , …, Хm : |
|
|
|
|
|
|
|
|||
σ11 DХ1 , σ22 DХ 2 , …, σmm DХ m .
Оценки для математических ожиданий найдутся как средние арифметические:
|
|
n |
|
|
|
|
Х |
k (n) xki / n, |
k 1, n . |
||
|
|
i 1 |
|
|
|
Несмещенные оценки для дисперсий определяются по формулам

|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
S 2 |
(n) (x |
ki |
|
Х |
k |
(n))2 /(n 1) |
, |
|
|
|||||||||||
|
|
|
k |
|
i1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
а для ковариаций – по формулам |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
σˆkl (xki |
Х |
k |
(n))(xli |
Х |
l (n)) /(n 1). |
||||||||||||||||
|
|
|
i 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
По этим данным определяются также оценки для элементов |
|||||||||||||||||||||||
корреляционной матрицы |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
σˆkl |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
ρˆ |
kl |
|
, где S |
k |
|
S 2 (n), |
S |
l |
|
S 2 (n). |
|||||||||||||
|
|
||||||||||||||||||||||
|
|
Sk Sl |
|
|
|
|
|
|
|
|
|
k |
|
|
|
l |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример 3.14. Ниже в таблице приведены результаты опытов, в которых исследовалась зависимость глубины h (мм) проникновения снаряда в преграду от удельной энергии ε (т.е. энергии, приходящейся на 1 см2 площади соударения). Найти все вышеперечисленные оценки, а также построить эмпирические линии регрессии.
Решение. Находим несмещенные оценки:
|
|
13 |
|
|
|
|
|
|
|
|
|
|
|
13 |
|
|
|
|
|
|
|
|
|
||
ε ( εi) /13 164,46; |
|
|
|
h |
( hi ) /13 21,08; |
|
|||||||||||||||||||
|
|
i 1 |
|
|
|
|
|
|
|
|
|
|
|
i1 |
|
|
|
|
|
|
|
|
|
||
|
|
13 |
|
|
|
|
|
|
|
|
|
|
|
|
13 |
hi |
|
|
2 |
|
|
|
|||
Sε2 εi ε 2 |
/12 6660,19; |
|
|
Sh2 |
|
|
h |
/12 103,84; |
|||||||||||||||||
σˆ |
|
i 1 |
|
|
ε h h /12 826,62; |
|
|
i1 |
|
|
σˆ h 0,994; |
|
|||||||||||||
|
ε |
|
|
|
ρˆ |
|
|||||||||||||||||||
|
h |
13 |
|
i |
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
i 1 |
|
|
|
|
|
|
|
|
|
|
|
|
S Sh |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
ˆ |
|
ρˆSε /Sh 7,96; |
|
|
|
|
|
|
|
ˆ |
|
ρˆSh /Sε |
0,124. |
|
|||||||||||
βεh |
|
|
|
|
|
|
|
βhε |
|
||||||||||||||||
|
|
|
i |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
8 |
|
9 |
|
10 |
|
11 |
12 |
13 |
|||||
|
|
|
εi |
41 50 81 104 120 139 154 180 208 241 250 269 301 |
|||||||||||||||||||||
|
|
|
hi |
4 |
8 |
10 |
14 |
16 |
20 |
19 |
23 |
26 |
30 |
|
31 |
36 |
37 |
||||||||
После подстановки полученных оценок получим следующие эмпирические линии регрессии:
h на ε: h−21,08=0,124(ε−164,46); ε на h: ε−164,46=7,96(h−21,08).
Проверим эти расчеты с помощью программы « Statistica».

Рис. 3.16
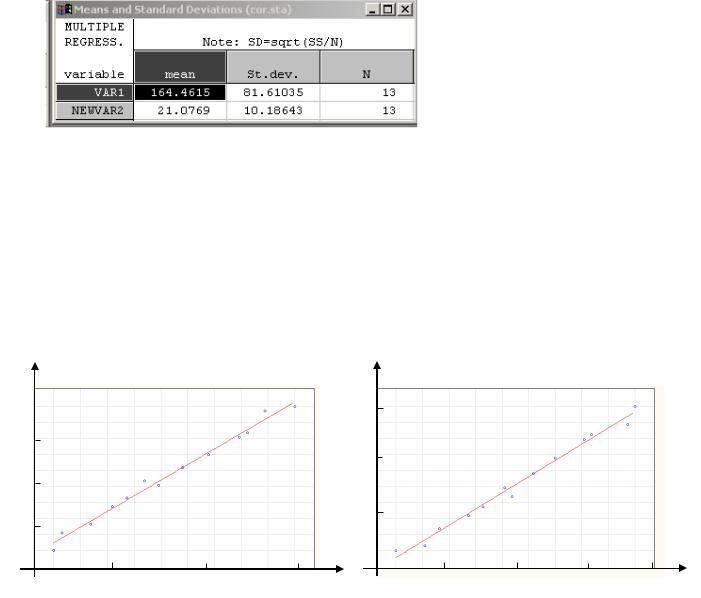
Рис. 3.17
Результаты расчетов совпадают, разница только в том, что в расчетах мы использовали несмещенные оценки, что не влияет на конечный результат.
Эмпирические линии регрессии h на ε и ε на h показаны на рис. 3.18, 3.19
h |
|
ε |
|
40 |
|
|
|
300 |
|||
|
|||
30
200
20
100
10
0 |
100 |
200 |
300 ε 0 |
10 |
20 |
30 |
40 h |
|
Рис. 3.18. |
|
Рис. 3.18 |
|
|
||
Результаты расчетов по программе «Statistica» подтверждают правильность проведенных расчетов.
3.12 Задание №2 на самостоятельную работу
3.1 Допустим, что данные о времени обслуживания (мин.), представленные в таблице 3.9, являются независимыми наблюдениями относительно времени обслуживания в системе массового обслуживания с одним устройством. Используя все подхо дящие методы, описанные в разделе 3 , построить гипотезу относительно формы распределения, определить оценки его параметра (параметров) с помощью оценок максимального правдоподобия и определить степень согласия.
Таблица 3.9
0,02 |
3,37 |
1,92 |
3,09 |
4,21 |
11,31 |
2,93 |
0,86 |
2,54 |
3,23 |
8,52 |
1,39 |
5,83 |
2,28 |
0,37 |
2,82 |
2,57 |
5,12 |
5,08 |
1,58 |
2,08 |
4,95 |
5,02 |
0,72 |
2,50 |
2,66 |
4,56 |
1,99 |
8,22 |
5,16 |
3,19 |
1,15 |
3,57 |
3,04 |
0,89 |
3,34 |
0,99 |
7,15 |
10,29 |
1,04 |
5,79 |
6,88 |
2,19 |
|
3,45 |
3,43 |
3,79 |
2,83 |
5,08 |
4,73 |
3,27 |
1,36 |
7,12 |
1,65 |
|
1,35 |
4,33 |
6,03 |
4,45 |
2,07 |
5,00 |
2,66 |
0,51 |
0,94 |
1,52 |
|
0,83 |
4,04 |
2,80 |
3,78 |
0,84 |
4,19 |
2,14 |
4,46 |
7,02 |
3,67 |
|
4,39 |
4,85 |
5,97 |
7,66 |
4,85 |
1,03 |
7,23 |
6,36 |
3,29 |
5,49 |
|
4,39 |
4,75 |
2,10 |
6,03 |
2,39 |
4,05 |
3,43 |
3,14 |
3,35 |
0,71 |
|
7,78 |
16,44 |
2,82 |
3,41 |
4,06 |
6,64 |
3,07 |
1,95 |
2,34 |
3,46 |
|
2,66 |
6,71 |
3,47 |
1,16 |
5,03 |
2,12 |
7,98 |
2,13 |
10,79 |
3,26 |
|
3.2 Предположим, что данные о погрешностях в диаметре шарикоподшипников, представленные в табл. 3.10, являются независимыми наблюдениями относительно отклонений от требуемого диаметра шарикоподшипников, изготовляемых на новом высокоскоростном станке. Используя все подходящ ие методы, описанные в разделе 3 , построить гипотезу относительно формы распределения, определить оценки его параметра (параметров) с помощью оценок максимального правдоподобия и степен ь согласия.
Табл. 3.10
2,31 |
0,56 |
2,73 |
1,50 |
1,00 |
2,54 |
1,51 |
2,24 |
1,18 |
1,23 |
1,74 |
1,49 |
0,38 |
1,33 |
0,17 |
0,19 |
1,55 |
1,06 |
1,06 |
1,59 |
2,26 |
0,78 |
2,10 |
0,77 |
0,26 |
1,55 |
2,28 |
0,49 |
2,04 |
1,75 |
1,63 |
1,06 |
1,01 |
0,30 |
2,29 |
3,11 |
1,48 |
0,01 |
1,62 |
1,64 |
2,21 |
0,44 |
1,13 |
1,63 |
0,48 |
1,55 |
0,99 |
1,97 |
0,31 |
2,40 |
1,68 |
1,71 |
2,44 |
1,98 |
1,62 |
1,71 |
0,27 |
0,24 |
0,59 |
−0,12 |
0,59 |
3,21 |
1,96 |
2,20 |
0,89 |
0,46 |
0,19 |
1,62 |
1,35 |
1,15 |
0,89 |
2,18 |
2,72 |
1,69 |
2,30 |
0,48 |
2,08 |
0,00 |
0,94 |
0,60 |
0,95 |
0,60 |
1,14 |
2,14 |
1,78 |
1,30 |
4,01 |
1,70 |
0,66 |
0,94 |
1,17 |
0,45 |
0,21 |
1,21 |
0,70 |
−0,67 |
0,22 |
0,28 |
2,05 |
−1,27 |
1,20 |
1,12 |
−0,51 |
1,90 |
1,43 |
1,28 |
2,29 |
1,09 |
1,50 |
0,02 |
1,01 |
0,26 |
2,79 |
2,36 |
1,10 |
2,02 |
1,23 |
1,26 |
3,27 |
1,47 |
−0,05 |
−0,54 |
1,40 |
0,17 |
1,03 |
0,85 |
1,82 |
0,06 |
1,12 |
0,49 |
−1,72 |
1,85 |
1,70 |
2,12 |
0,44 |
0,24 |
1,09 |
1,11 |
1,00 |
−0,16 |
1,08 |
−1,62 |
1,50 |
2,58 |
1,41 |
0,78 |
2,66 |
1,99 |
2,69 |
1,37 |
1,71 |
0,77 |
1,87 |
0,49 |
3.3 Пусть имеется нормально распределенная случайная величина Х. Произведено N = 31 независимых наблюдений этой величины, ре - зультаты которых приведены в табл. 3 .11.
Табл.3.11
60 |
55 |
53 |
69 |
58 |
47 |
56 |
58 |
59 |
62 |
61 |
67 |
67 |
61 |
58 |
54 |
65 |
60 |
61 |
61 |
59 |
54 |
57 |
56 |
48 |
61 |
43 |
57 |
63 |
65 |
62 |
|
Определить 90% -е доверительные интервалы для истинного сред него значения и истинной дисперсии случайной величины Х.
Ответ: 90%-ные доверительные интервалы для среднего значения и дисперсии случайной величины Х составляют
56,85 < mх <60,37,
22,91 < σ2x < 54,22.
3.4 Предположим, что есть основания считать среднее значение mx случайной величины Х равным 10, и пусть известна дисперсия величины
Х, σ2x 4 . Определить, каков должен быть объем выборки для проверки
гипотезы mx = 10 при 5%-м уровне значимости, причем вероят ность допустить ошибку второго рода при определении 10% -го отклонения от гипотетической величины также должна соста вить 5%. Определить при этих условиях область принятия, ко торую следует использовать при проверке гипотезы.
Ответ: искомый объем выборки N=52. Область принятия гипотезы
9,46 < mx < 10,54.
3.5 Проверка гипотезы о нормальности распределения. В табл.2.12 приведены N=200 независимых наблюден ных значений, расположенных в порядке возрастания процесса на выходе генератора теплового шума.
Пример выполнения задания приведен ниже.
Задание 1. Допустим, что данные о времени обслуживания (мин.), представленные в таблице 1, являются независимыми наблюдениями относительно времени обслуживания в системе массового обслуживания с одним устройством. Используя все подходящие методы, описанные в разделе математической статистики (р.3), построить гипотезу относительно формы распределения, определить оценки его параметра (параметров) с помощью оценок максимального правдоподобия и определить степень согласия.
Таблица 1
0,02 |
3,37 |
1,92 |
3,09 |
4,21 |
11,31 |
2,93 |
0,86 |
2,54 |
3,23 |
8,52 |
1,39 |
5,83 |
2,28 |
0,37 |
2,82 |
2,57 |
5,12 |
5,08 |
1,58 |
2,08 |
4,95 |
5,02 |
0,72 |
2,50 |
2,66 |
4,56 |
1,99 |
8,22 |
5,16 |
3,19 |
1,15 |
3,57 |
3,04 |
0,89 |
3,34 |
0,99 |
7,15 |
10,29 |
1,04 |
5,79 |
6,88 |
2,19 |
|
3,45 |
3,43 |
3,79 |
2,83 |
5,08 |
4,73 |
3,27 |
1,36 |
7,12 |
1,65 |
|
1,35 |
4,33 |
6,03 |
4,45 |
2,07 |
5,00 |
2,66 |
0,51 |
0,94 |
1,52 |
|
0,83 |
4,04 |
2,80 |
3,78 |
0,84 |
4,19 |
2,14 |
4,46 |
7,02 |
3,67 |
|
4,39 |
4,85 |
5,97 |
7,66 |
4,85 |
1,03 |
7,23 |
6,36 |
3,29 |
5,49 |
|
4,39 |
4,75 |
2,10 |
6,03 |
2,39 |
4,05 |
3,43 |
3,14 |
3,35 |
0,71 |
|
7,78 |
16,44 |
2,82 |
3,41 |
4,06 |
6,64 |
3,07 |
1,95 |
2,34 |
3,46 |
|
2,66 |
6,71 |
3,47 |
1,16 |
5,03 |
2,12 |
7,98 |
2,13 |
10,79 |
3,26 |
|
Проверка гипотезы о независимости признаков:
Analysis - Tables and banners - в окне Specify Table, в поле Analysis: Crosstabulation tables - кнопка Specify Table - отбираем признаки,- в окне Crosstabulation Tables Results (результаты таблиц сопряженности) отмечаем (потребуем определить)
Expected frequencies (ожидаемые или теоретические частоты) и Pearson Chi-Square - Review Summary tables.
Проверка гипотезы о типе распределения. Работаем в модуле Nonparametric Statistics (непараметрическая статистика), Distribution Fitting (подбор распределения). В поле Continuous Distributions: Normal - Variable: d - в поле Plot distribution: Frequency distribution (частоты распределения) - отказываемся от теста Колмогорова - Смирнова - ОК - наблюдаем оценки параметров Mean: 13.42, Variance: 0.018, соглашаемся с параметрами группирования (в частности, c числом групп Number of categories: 19) - ОК.
Наблюдаем таблицу частот, в которой нам нужны столбцы observed frequency (наблюдаемые частоты) и expected frequency (ожидаемые частоты). Сравним графически наблюдаемые и ожидаемые частоты: выделим соответствующие столбцы - Graphs - Custom Graphs - 2D Graphs...- OK.. Наблюдаем некоторое различие.

Аналогично Задание 2

3. Пусть имеется нормально распределенная случайная величина Х. Произведено N = 31 независимых наблюдений этой величины, результаты которых приведены в табл. 3.
Табл.3
60 |
55 |
53 |
69 |
58 |
47 |
56 |
58 |
59 |
62 |
61 |
67 |
67 |
61 |
58 |
54 |
65 |
60 |
61 |
61 |
59 |
54 |
57 |
56 |
48 |
61 |
43 |
57 |
63 |
65 |
62 |
|
Определить 90% -е доверительные интервалы для истинного среднего значения и истинной дисперсии случайной величины
Х.
Ответ: 90%-ные доверительные интервалы для среднего значения и дисперсии случайной величины Х составляют
56,85 < mх <60,37,
22,91 < σ2x < 54,22

4. Проверка гипотезы о нормальности распреде ления. В табл.4 приведены N=200 независимых наблюден ных значений, расположенных в порядке возрастания процесса на выходе генератора теплового шума.
Табл. 4
−7,6 − 4,3 − 3,0 − 2,1 − 1,5 − 0,7 0,0 0,7 1,5 2,3 3,4 4,3 6,3
−6,9 − 4,1 − 3,0 − 2,1 − 1,4 − 0,7 0,1 0,8 1,5 2,4 3,5 4,3 6,5
−6,6 − 4,0 − 2,9 − 2,0 − 1,4 − 0,6 0,1 0,9 1,6 2,4 3,5 4,4 6,9
−6,4 − 3,8 − 2,9 − 2,0 − 1,2 − 0,6 0,2 0,9 1,6 2,5 3,6 4,4 7,1
−6,4 − 3,8 − 2,9 − 1,9 − 1,2 − 0,5 0,2 1,0 1,6 2,5 3,6 4,6 7,2
−6,1 − 3,8 − 2,7 − 1,9 − 1,2 − 0,5 0,2 1,0 1,7 2,6 3,6 4,8 7,4
−6,0 − 3,7 − 2,6 − 1,8 − 1,1 − 0,4 0,2 1,1 1,8 2,6 3,7 4,8 7,9
−5,7 − 3,6 − 2,6 − 1,8 − 1,1 − 0,4 0,3 1,1 1,8 2,6 3,7 4,9 9,0
−5,6 − 3,5 − 2,5 − 1,8 − 1,0 − 0,4 0,3 1,1 1,8 2,7 3,7 5,0
−5,5 − 3,4 − 2,5 − 1,7 − 1,0 − 0,3 0,3 1,1 1,9 2,8 3,7 5,2
−5,1 − 3,4 − 2,4 − 1,7 − 1,0 − 0,3 0,4 1,2 1,9 2,8 3,8 5,3
−4,8 − 3,4 − 2,3 − 1,6 − 0,9 − 0,2 0,4 1,2 2,0 2,9 3,8 5,4
−4,8 − 3,3 − 2,3 − 1,6 − 0,9 − 0,2 0,5 1,3 2,0 3,1 3,9 5,6
−4,6 − 3,2 − 2,3 − 1,6 − 0,8 − 0,2 0,5 1,3 2,1 3,2 4,0 5,9
−4,4 − 3,2 − 2,2 − 1,6 − 0,8 − 0,1 0,6 1,3 2,3 3,2 4,2 6,1
− 4,4 − 3,1 − 2,2 − 1,5 − 0,7 0,0 0,6 1,4 2,3 3,3 4,2 6,3
Проверить гипотезу о нормальности процесса на выходе генератора теплового шума, применяя критерий согласия χ2 при уровне значимости α = 0,05. Использовать равновероятный подход к определению значения критерия χ2 , положив k = 16
